2024-3S 計算数理演習（東京大学理学部・教養学部） [齊藤宣一] [top] [0] [1] [2] [3] [4] [5] [6] [7] [8] [UTOL]

0. ガイダンス

担当者

講義の形式

本講義は，駒場情報教育棟（E41）での対面型の講義として行います．

一方で，講義はすべて，Zoomを通じてリアルタイムにストリーミング配信します．また，Zoomの録画を（受講生にのみ）公開します．対面講義に参加が難しい学生は，これらの方法を利用して，オンラインで講義を受けることが可能です．（いわゆるハイフレックス型講義です）

出席はとりません．

講義の概要

動機1

代数方程式 $z^n+a_{n-1}z^{n-1}+\cdots+a_1z+a_0=0$ の根の数値を求めたい．

根の公式を使えば良い？
- カルダーノ(Cardano)の公式: $x^3+px+q=0$ の根の一つは， $x= \sqrt[3]{-\frac{q}{2}+\sqrt{\frac{q^2}{4}+\frac{p^3}{27}}}+ \sqrt[3]{-\frac{q}{2}-\sqrt{\frac{q^2}{4}+\frac{p^3}{27}}}$.
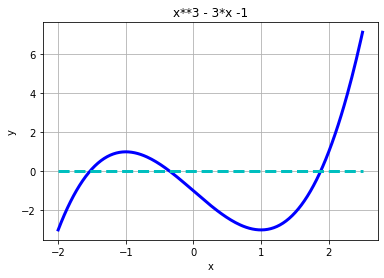
- $f(x)=x^3-3x-1=0$ に適用すると， $x=\sqrt[3]{\frac12+ i\sqrt{\frac34}}+\sqrt[3]{\frac12- i\sqrt{\frac34}}$ となる．
具体的な数値（近似解）が知りたい

構成的な解法としての反復解法 $x_{k+1}=\varphi(x_k)$ が便利．関数 $\varphi$ を $\lim_{k\to\infty}x_k=\mbox{ 根 }$ となるように構成したい．
Newton法が有名

動機2

有界閉区間 $[a,b]$ 上の連続関数 $f(x)$ に対して，$\displaystyle{\int_a^bf(x)~dx}$ の値を求めたい．

原始関数がわからない場合どうするか？ほとんどの場合!

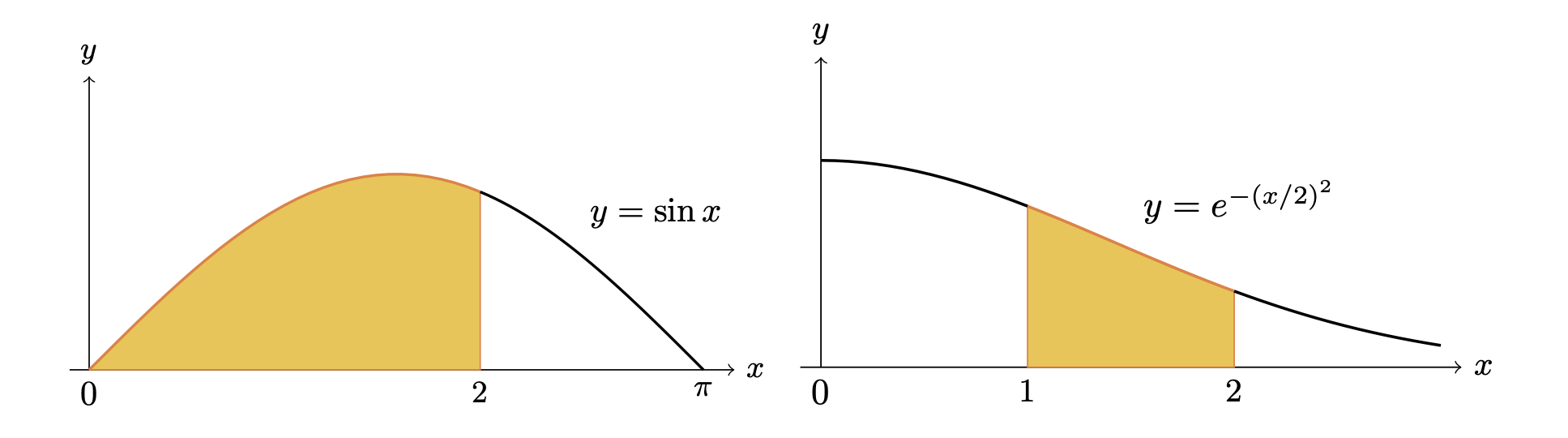
動機3

競合の関係下にある2種類の生物の増殖の数理モデル（Lotoka-Volterra微分方程式系） \[ \displaystyle{\frac{du_1}{dt}} = c_1u_1(1-b_1u_1-d_2u_2),\qquad \displaystyle{\frac{du_2}{dt}} = -c_2u_2(1-b_2u_2-d_1u_1) \] の解について，$u_1(t)$ と $u_2(t)$ の時間変化が知りたい．ここで，$u_1(t)$ と $u_2(t)$ は2種類の生物の個体密度， $c_1,c_2$ はそれぞれの生物の増殖係数，さらに，$b_1,b_2,d_1,d_2$ は，互いの競合の関係や，環境の影響を表現する定数である．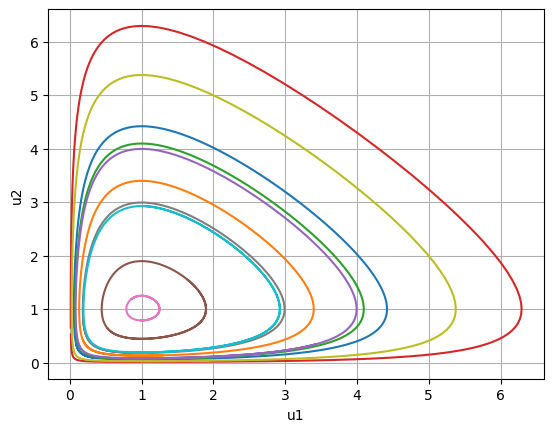

動機4

偏微分方程式，特に，熱方程式や波動方程式 \[ \frac{\partial u}{\partial t}= \kappa \frac{\partial^2 u}{\partial x^2},\qquad \frac{\partial^2 u}{\partial t^2}=c^2 \frac{\partial^2 u}{\partial x^2} \] の解を可視化したい．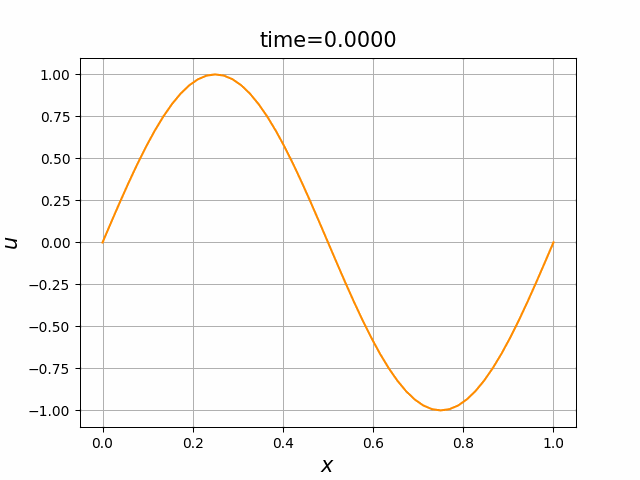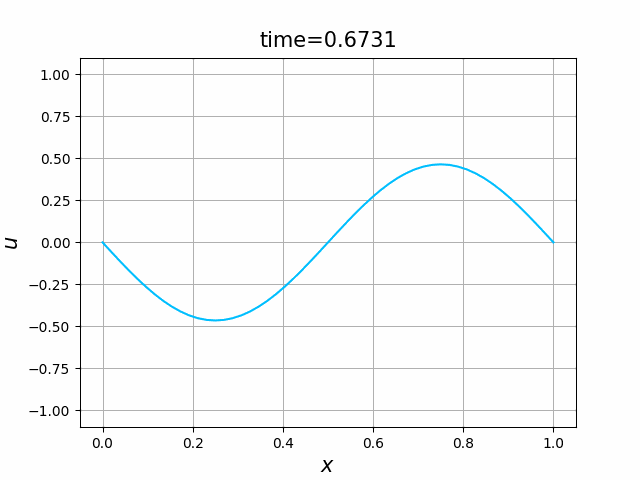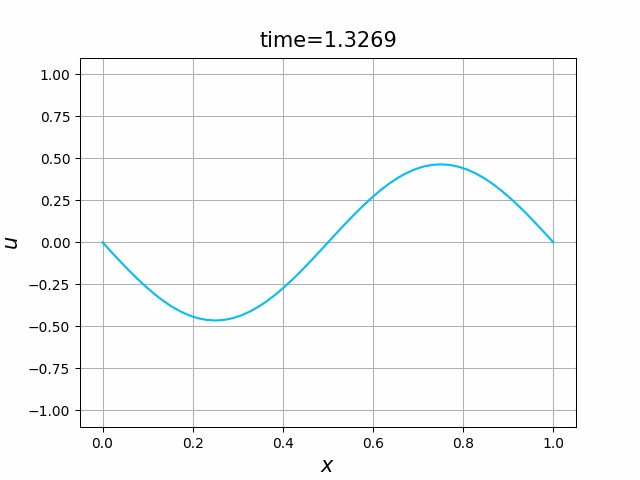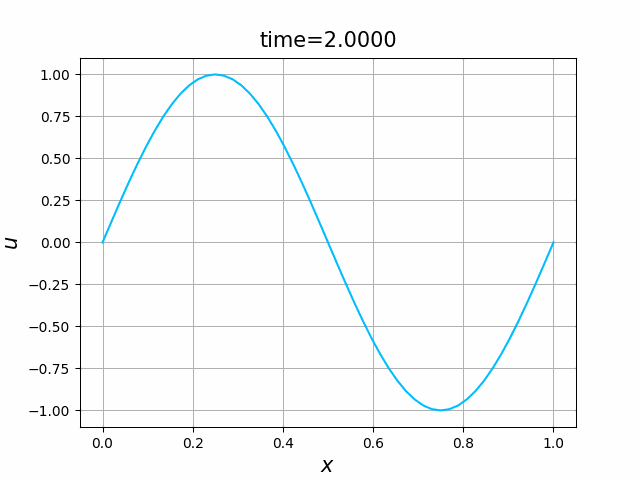

本講義の目標

本講義では，数学的問題の解を具体的に計算する（$=$数値を得る）方法を研究する．このような分野には，いろいろな呼び方がある．

数値解析 (numerical analysis)
数値計算 (numerical computation)
計算数理 (computational mathematics)
科学計算 (scientific computing)

もう少し大きな分類では，応用数学の一部になる．

一つの行き先： https://www.youtube.com/watch?v=267HdDdIywI

ただし，この講義は，より数学的な部分を強調します．

キーワードは，連続と離散．

スケジュールと方法

4月5日ガイダンス（オンラインとオンデマンドのみ）
4月19日 1. Pythonによる数値計算の基礎
4月26日 2. Pythonによる数値計算の基礎（浮動小数点数の演算）
5月10日 3. 非線形方程式の求解
5月15日 4. 数値積分
5月17日レポート作成日
5月24日レポート作成日
6月7日 5. 固有値問題
6月14日 6. 常微分方程式の初期値問題（基礎編）
6月21日 7. 微分方程式の初期値問題（応用編）
6月28日レポート作成日（オンラインのみ）
7月5日 8. 偏微分方程式：熱伝導，波動の数値計算
7月12日レポート作成日

本講義では，提示された課題に対して，受講生が自ら作成したプログラムを用いて，数値計算を行い，理論との比較検討の考察を行ってもらいます．ただし，いずれの課題についても，数値計算法の説明をした上で，たたき台となるサンプルプログラムを提示して，計算を実演します．サンプルプログラムは， Google colaboratoryを用いてPythonで作成します．ネットワークに繋がる環境で受講できれば，計算環境を自分で整える必要はありません．

講義は毎回，次のように行います．

各項目について，説明と実演をする．
受講生は，各項目の問題と課題に各自で取り組む．受講生同士での議論，情報交換を歓迎する．
ただし，説明にそれなりに時間がかかるので，受講生が計算課題に取り組む時間はそう多くない．そのため，「レポート作成日」を設ける．
レポート作成日については，受講生が主体的に，計算に取り組み，質問や討議を通じて，理解を深める．

本講義の目標は，Pythonの修得ではありません．あくまで，数値計算の道具の代表例として利用します．受講生は，他の言語や（Matlabなどの）ソフトウエアを用いても構いません．また，Google colaboratoryを利用せず，受講者自身のPythonプログラミング環境で計算を行っても結構です．

Pythonについて，巷では色々な評価があります．私は，簡単に，色々なことができて便利であると思います．利用者が自分で環境構築をしなくても良い（環境が利用できる）ところにも，お得感があります．

注意

金曜2限の計算数理I（理学部），計算数理（教養学部）の履修を，強く勧めます．

成績評価とレポートの提出

成績評価はレポートによる：前半1回（6月7日締切を予定），後半1回（7月26日締切を予定）
一つのレポートについて，課題2つ分を報告してもらう．課題は，各項目について1〜3個ある．その中から，2題を選択するということ．
前半に出してもらったレポートのうち，良いものについては，講義中に紹介します．

レポートの形式

レポートは，PDF形式（*****.pdf）のファイルで，UTOLのレポート登録機能を通じて提出されたもののみを受け付ける．

レポートの構成は次のようにすること：

名前と所属学科
課題の内容（改めて自分で簡単にまとめる）
計算に使用したプログラム（適宜省略可．簡単な説明も付けた方が良い）
計算結果のまとめ（入力と出力など）
結果に対する考察（理論通り／異なる，予想通り／異なる，など）
図や表を入れるとわかりやすいが，あまり凝り過ぎると，締め切りに間に合わなくなります．

（数学とは関係のないことなので）レポートを作成するソフトウエアは，なんでも良い．例えば，WORD，PowerPoint，Googleドキュメントなどを使っても良い．

しかし，せっかくの機会なので，LaTeX の利用を勧める．すでに，LaTeX を利用している人は，自分の使いやすい環境でレポートを作成して良い．

利用経験のない人には，次が便利である．

Cloud LaTeX (https://cloudlatex.io/)
Overleaf (https://ja.overleaf.com/)

これらは，Web上ですべての作業ができるので，インストールは不要で，自分のPCはもちろん，どんな場所ででも利用できる．初心者には，Cloud LaTeXが便利であろう．UTOLの教材の中に，簡易的なLaTeXのマニュアルを用意した．適宜，活用してほしい．

参考書

教科書は特に指定しません．例題を

S. Linge and H. P. Langtangen, Programming for Computations---Python (2nd edition), Springer, 2020

から拝借することがあります。数値計算法の数理については、以下が参考になります：

A. Quarteroni, F. Saleri, P. Gervasio, Scientific Computing with MATLAB and Octave (4th edition), Springer, 2014（加古孝，千葉文浩訳，MATLABとOctaveによる科学技術計算，丸善出版，2014年）
齊藤宣一，数値解析入門（大学数学の入門9），東京大学出版会，2012年
齊藤宣一，偏微分方程式の計算数理，共立出版，2023年

Pythonを用いた数値計算については，次が参考になります：

大槻純也，Pythonによる計算物理，森北出版，2023年

---「0. ガイダンス」はこれで終了---