2024-3S 計算数理演習(東京大学理学部・教養学部) [齊藤宣一] [top] [0] [1] [2] [3] [4] [5] [6] [7] [8] [UTOL]
5. 固有値問題
$A\in\mathbb{C}^{n\times n}$($=n\times n$ 複素行列全体の集合) に対する固有値問題 \[ \lambda\in\mathbb{C},\quad \boldsymbol{0}\ne\boldsymbol{v}\in\mathbb{C}^{n},\quad A\boldsymbol{v}=\lambda\boldsymbol{v} \] を考察する.$\lambda_1,\ldots,\lambda_n\in\mathbb{C}$ を $A$ の固有値, $\boldsymbol{v}_1,\ldots,\boldsymbol {v}_n$ を対応する固有ベクトルとする. さらに,$|\lambda_1|\le|\lambda_2|\le\cdots \le |\lambda_n|$ と並べておく.
例5.1
例題として, $\displaystyle{ A=\begin{pmatrix} 5 & 4 & 1 & 1\\ 4 & 5 & 1 & 1\\ 1 & 1 & 4 & 2\\ 1 & 1 & 2 & 4 \end{pmatrix}}$ を考える.絶対値最大の固有値は $\lambda_4=10$,(正規化された)固有ベクトルは, $\displaystyle{\boldsymbol{v}_4 =\begin{pmatrix} 2/\sqrt{10}\\ 2/\sqrt{10}\\ 1/\sqrt{10}\\ 1/\sqrt{10} \end{pmatrix} \approx \begin{pmatrix} 0.6325\\ 0.6325\\ 0.3162\\ 0.3162 \end{pmatrix} }$ となる. 答えがわかっているのだから,近似計算をする必要はないが,近似解法の妥当性を確認するために,あえて,答えのわかっている問題で試すのである.$\blacksquare$
固有値と固有ベクトルを求めることは, numpyの linalgを用いれば容易い.
In [1]: import numpy as np import matplotlib.pyplot as plt from numpy import linalg as la
In [2]:
A=np.array([[5,4,1,1], [4,5,1,1],[1,1,4,2],[1,1,2,4]])
eval, evect = np.linalg.eig(A)
print("eigenvalues\n",eval)
print("eigenvectors\n",evect)
print("eigenvalue\n",eval[0])
print("eigenvector\n",evect[:,0])
Out [3]:
eigenvalues
[10. 1. 5. 2.]
eigenvectors
[[-6.32455532e-01 -7.07106781e-01 3.16227766e-01 1.66533454e-16]
[-6.32455532e-01 7.07106781e-01 3.16227766e-01 -6.74454005e-17]
[-3.16227766e-01 -5.94276718e-17 -6.32455532e-01 -7.07106781e-01]
[-3.16227766e-01 -8.70027738e-17 -6.32455532e-01 7.07106781e-01]]
eigenvalue
9.999999999999996
eigenvector
[-0.63245553 -0.63245553 -0.31622777 -0.31622777]
関数eigをブラックボックス的に使うのであれば,それ以上考察することはない.しかし,本節では,「具体的にどのようなアルゴリズムで固有値を計算することができるのか」および「その数学的妥当性」を検討する.
固有値を求めるには,最も素朴には,固有多項式を構成して,Newton法を適用することが考えられる.しかし,$n$ が大きい時には,実用的でない.
本節では,固有値(実は固有ベクトル)の代表的な近似計算方法である冪乗法と逆冪乗法を紹介する.これらは,特定の固有値を求める方法である. 一方で,すべての固有値を同時に求める方法もある.QR法はその代表である. 実は,関数eigでは,QR法に基づいた方法で計算を行っている.QR法については,最後に簡単に述べる.
以下では,次の記号を用いる.
- $\mathbb{C}^n$の内積 $\displaystyle{\langle\boldsymbol{x},\boldsymbol{y}\rangle=\sum_{i=1}^nx_i\overline{y_i}} \quad (\boldsymbol{x}=(x_i),~\boldsymbol{y}=(y_i)\in\mathbb{C}^n)$
- $\mathbb{C}^n$ のノルム $\displaystyle{\|\boldsymbol{x}\|= \left(\sum_{i=1}^n|x_i|^2 \right)^{1/2}}$
- Rayleigh商 $\displaystyle{R_A(\boldsymbol{x})= \frac{\langle A\boldsymbol{x},\boldsymbol{x}\rangle}{~\|\boldsymbol{x}\|^2}\in\mathbb{C}} \quad (\boldsymbol{x}\ne \boldsymbol{0})$
- $\|\boldsymbol{x}\|^2=\langle\boldsymbol{x},\boldsymbol{x}\rangle$
- Cauchy--Schwarzの不等式 $|\langle\boldsymbol{x},\boldsymbol{y}\rangle|\le \|\boldsymbol{x}\|\|\boldsymbol{y}\|$
- $A\boldsymbol{v}=\lambda\boldsymbol{v}$,$\boldsymbol{v}\ne\boldsymbol{0}$ ならば,$R_A(\boldsymbol{v})=\lambda$.(固有ベクトルが得られれば,Rayleigh商により固有値が算出できる.)
- 任意の $0\ne \alpha\in\mathbb{C}$ に対して, $R_A(\alpha\boldsymbol{x})=R_A(\boldsymbol{x})$.
- $A$ がエルミートならば,$R_A(\boldsymbol{x})\in\mathbb{R}$.
冪乗法
$A$ に対して,次を仮定する: \begin{equation} \tag{$\star$} |\lambda_1| \le \cdots \le |\lambda_{n-1}|<|\lambda_n|\quad \mbox{かつ}\quad \mbox{$A$ は対角化可能}. \end{equation} そして,絶対値が最大の固有値 $\lambda_n$ を求める.
$\boldsymbol{x}\in\mathbb{C}^n$ を任意とし, $\boldsymbol{x}=c_1\boldsymbol{v}_1+\cdots+c_n\boldsymbol{v}_n$ と書く(「$A$は対角化可能 $\Leftrightarrow$ $\boldsymbol{v}_1,\ldots,\boldsymbol{v}_n$ は一次独立」に注意せよ).$1\le k\in \mathbb{Z}$ に対して, \begin{align*} \boldsymbol{x}' &\stackrel{\textrm{def.}}{=} A^k\boldsymbol{x}\\ &= c_1\lambda_1^k\boldsymbol{v}_1+\cdots+c_n\lambda_n^k\boldsymbol{v}_n \nonumber \\ &= c_n\lambda_n^k \left[\frac{c_1}{c_n}\left(\frac{\lambda_1}{\lambda_n}\right)^k\boldsymbol{v}_1+\cdots+\frac{c_{n-1}}{c_n} \left(\frac{\lambda_{n-1}}{\lambda_n}\right)^k\boldsymbol{v}_{n-1}+\boldsymbol{v}_n\right] \end{align*} となるので,$c_n\ne 0$ かつ $k$ が十分大きければ, \[ \boldsymbol{x}'\approx \lambda_n^kc_n\boldsymbol{v}_n \] が期待できる.そして, $R_A(\lambda_n^kc_n\boldsymbol{v}_n)=R_A(\boldsymbol{v}_n)=\lambda_n$ なので, この関係により,近似固有値 $\tilde{\lambda}=R_A(\boldsymbol{x}')$ を得ることができる.
冪乗法のアルゴリズム
$\boldsymbol{x}^{(0)}\in\mathbb{C}^n$ を初期値として, 次のように点列 $\boldsymbol{x}^{(k)}$ ($k=1,2,\ldots$) を生成する: \[ \boldsymbol{y}^{(k)}=A\boldsymbol{x}^{(k)},\quad \boldsymbol{x}^{(k+1)}=\frac{1}{\|\boldsymbol{y}^{(k)}\|}\boldsymbol{y}^{(k)}. \] このとき,近似固有値は $\mu^{(k)}=R_A(\boldsymbol{x}^{(k)})$ で与えられる.$\blacksquare$
注意. 単純に,$\boldsymbol{x}^{(k+1)}=A\boldsymbol{x}^{(k)}$ とすると,ほとんどの場合,$\|\boldsymbol{x}^{(k)}\|\to\infty$ あるいは $\|\boldsymbol{x}^{(k)}\|\to 0$ となる.一方で,必要なのは $\boldsymbol{x}^{(k)}$ の向きに関する情報のみである.
注意. 明らかに,$\|\boldsymbol{x}^{(k)}\|=1$ $(k\ge 1)$ となる.
冪乗法のプログラムの例をIn [3]に示す.
In [3]:
def power1(A, initial, tolerance):
kmax = 100
eval = np.array([])
increment = np.array([])
evec = np.copy(init)
k = 0
x = initial / la.norm(initial, ord=2)
muold = 0
inc = tolerance + 1
while k <= kmax and inc >= tolerance:
y = A@x
mu = np.vdot(y, x)
inc = np.abs((mu - muold) / mu)
eval = np.append(eval, mu)
increment = np.append(increment, inc)
evec = np.vstack((evec, x))
x = y / la.norm(y, ord=2)
muold = mu
k += 1
return k, eval, increment, evec[1:,:]
まずは,ともかく実行してみよう.
In [4]:
A=np.array([[5,4,1,1], [4,5,1,1],[1,1,4,2],[1,1,2,4]])
init = np.array([1, 0, 0, 0]) # 初期ベクトル
tol = 1e-8 # 許容誤差
iteration, eval, increment, evec = power1(A, init, tol)
print("反復, 固有値, 増分, 固有ベクトル")
for i in range(iteration):
print(f"{i:d}, {eval[i]:.4f}, {increment[i]:.3e}, ",evec[i,:])
Out [4]:
反復, 固有値, 増分, 固有ベクトル
0, 5.0000, 1.000e+00, [1. 0. 0. 0.]
1, 9.6047, 4.794e-01, [0.76249285 0.60999428 0.15249857 0.15249857]
2, 9.9220, 3.198e-02, [0.67459799 0.65890967 0.23532488 0.23532488]
3, 9.9805, 5.867e-03, [0.65173824 0.65016019 0.27616027 0.27616027]
4, 9.9951, 1.460e-03, [0.64210325 0.64194522 0.29631888 0.29631888]
5, 9.9988, 3.658e-04, [0.6373267 0.63731089 0.30630826 0.30630826]
6, 9.9997, 9.153e-05, [0.63490748 0.6349059 0.31127721 0.31127721]
7, 9.9999, 2.289e-05, [0.63368604 0.63368588 0.31375484 0.31375484]
8, 10.0000, 5.722e-06, [0.63307196 0.63307195 0.3149919 0.3149919 ]
9, 10.0000, 1.431e-06, [0.63276405 0.63276405 0.31560998 0.31560998]
10, 10.0000, 3.576e-07, [0.63260986 0.63260986 0.31591891 0.31591891]
11, 10.0000, 8.941e-08, [0.63253272 0.63253272 0.31607335 0.31607335]
12, 10.0000, 2.235e-08, [0.63249413 0.63249413 0.31615056 0.31615056]
13, 10.0000, 5.588e-09, [0.63247483 0.63247483 0.31618916 0.31618916]
確かに,絶対値最大の固有値とその固有ベクトルが,かなり正確に求められている.
このプログラムでは, 与えられたtoleranceに対して, \[ \mbox{inc}=\mbox{inc}_k\stackrel{\textrm{def.}}{=} \left| \frac{\mu_{k}-\mu_{k-1}}{\mu_{k}}\right|\le \mbox{tolerance} \] が満たされた時点で,これ以上反復を続けても数値が改善されないと判断して,計算を終了する.
技術的な注意を述べる.eval,increment,evec は, \[ \mbox{eval} =\begin{pmatrix} \mu_0\\ \mu_1\\ \vdots\\ \mu_m \end{pmatrix} ,\quad \mbox{increment} =\begin{pmatrix} \mbox{inc}_0\\ \mbox{inc}_1\\ \vdots\\ \mbox{inc}_m \end{pmatrix} ,\quad \mbox{evec} =\begin{pmatrix} \boldsymbol{x}_0^{\scriptsize \mbox{T}}\\ \boldsymbol{x}_1^{\scriptsize \mbox{T}}\\ \vdots\\ \boldsymbol{x}_m^{\scriptsize \mbox{T}} \end{pmatrix} \] である.ただし, $\mbox{inc}_{0}=1$ としており, $\mbox{inc}_{k+1}<\mbox{tolerance}$ を満たす最小の $k$ を $m$ と書いている. $\boldsymbol{x}_k^{\scriptsize \mbox{T}}$ は $\boldsymbol{x}_k$ の転置である.
これらを生成するため,最初に eval = np.array([]) により,空の配列としてevalを定義して,np.appendにより,最後尾に順に $\mu_0,\mu_1,\ldots$ を追加している. evecについても,np.vstackにより,最後尾(最終行)に順に $\boldsymbol{x}_0,\boldsymbol{x}_1,\ldots$ を追加している.ただし,np.vstackを利用する際には,対象となる配列の列数はすでに決定されていなければならない.そのため, evecを定義する際には, evec = np.copy(init)としている.しかし,このようにすると,最初の行(第0行)と次の行(第1行)に $\boldsymbol{x}_0$ が格納されることになる.したがって,計算結果を返す際に,evec[1:,:]として,第1行以降のみを返すようにしているのである.(もっと上手いやり方のわかる人は,ぜひ教えてください.)
In [5]: x = np.array([]) print(x.shape) print(x) x=np.append(x,2.0) print(x.shape) print(x) x=np.append(x,4.0) print(x.shape) print(x) y = np.array([[0, 0]]) y = np.vstack((y,[1,2])) print(y.shape) print(y) y=np.vstack((y,[3,4])) print(y.shape) print(y) Out [5]: (0,) [] (1,) [2.] (2,) [2. 4.] (2, 2) [[0 0] [1 2]] (3, 2) [[0 0] [1 2] [3 4]]
もう一つ,$\displaystyle{\mbox{np.vdot(y,x)}=\langle \boldsymbol{x},\boldsymbol{y}\rangle=\sum_{i=1}^n x_i\overline{y_i}}$ であることに注意せよ.
In [6]: x=np.array([1+2j,2-1j]) y=np.array([3-1j,4+5j]) print(np.vdot(x,y)) print(np.vdot(y,x)) Out [6]: (4+7j) (4-7j)
さて,改めて,初期ベクトルをかえて,冪乗法を実行してみよう.
In [7]:
init = np.array([1, 1, 1, 1]) # 初期ベクトル
tol = 1e-8 # 許容誤差
iteration, eval, increment, evec = power1(A, init, tol)
print("反復, 固有値, 増分, 固有ベクトル")
for i in range(iteration):
print(f"{i:d}, {eval[i]:.4f}, {increment[i]:.3e}, ",evec[i,:])
Out [7]:
反復, 固有値, 増分, 固有ベクトル
0, 9.5000, 1.000e+00, [0.5 0.5 0.5 0.5]
1, 9.8649, 3.699e-02, [0.5719 0.5719 0.4159 0.4159]
2, 9.9655, 1.010e-02, [0.604 0.604 0.3677 0.3677]
3, 9.9913, 2.584e-03, [0.6187 0.6187 0.3423 0.3423]
4, 9.9978, 6.498e-04, [0.6257 0.6257 0.3293 0.3293]
5, 9.9995, 1.627e-04, [0.6291 0.6291 0.3228 0.3228]
6, 9.9999, 4.069e-05, [0.6308 0.6308 0.3195 0.3195]
7, 10.0000, 1.017e-05, [0.6316 0.6316 0.3179 0.3179]
8, 10.0000, 2.543e-06, [0.632 0.632 0.3171 0.3171]
9, 10.0000, 6.358e-07, [0.6322 0.6322 0.3166 0.3166]
10, 10.0000, 1.589e-07, [0.6324 0.6324 0.3164 0.3164]
11, 10.0000, 3.974e-08, [0.6324 0.6324 0.3163 0.3163]
12, 10.0000, 9.934e-09, [0.6324 0.6324 0.3163 0.3163]
In [8]:
init = np.array([2, 2, 1, 1]) # 初期ベクトル
tol = 1e-8 # 許容誤差
iteration, eval, increment, evec = power1(A, init, tol)
print("反復, 固有値, 増分, 固有ベクトル")
for i in range(iteration):
print(f"{i:d}, {eval[i]:.4f}, {increment[i]:.3e}, ",evec[i,:])
Out [8]:
反復, 固有値, 増分, 固有ベクトル
0, 10.0000, 1.000e+00, [0.6325 0.6325 0.3162 0.3162]
1, 10.0000, 0.000e+00, [0.6325 0.6325 0.3162 0.3162]
ここまでは,順調である.しかし,次はどうであろうか?
In [9]:
init = np.array([1, 2, 3, -9]) # 初期ベクトル
tol = 1e-8 # 許容誤差
iteration, eval, increment, evec = power1(A, init, tol)
print("反復, 固有値, 増分, 固有ベクトル")
for i in range(iteration):
print(f"{i:d}, {eval[i]:.4f}, {increment[i]:.3e}, ",evec[i,:])
Out [9]:
反復, 固有値, 増分, 固有ベクトル
0, 2.7053, 1.000e+00, [ 0.1026 0.2052 0.3078 -0.9234]
1, 3.9824, 3.207e-01, [ 0.24 0.2742 -0.1028 -0.9255]
2, 4.7727, 1.656e-01, [ 0.3 0.3081 -0.4135 -0.8026]
3, 4.9612, 3.799e-02, [ 0.3133 0.315 -0.5479 -0.7088]
4, 4.9937, 6.516e-03, [ 0.3157 0.3161 -0.5994 -0.6641]
5, 4.9990, 1.055e-03, [ 0.3161 0.3162 -0.6194 -0.6453]
6, 4.9998, 1.691e-04, [ 0.3162 0.3162 -0.6273 -0.6376]
7, 5.0000, 2.706e-05, [ 0.3162 0.3162 -0.6304 -0.6345]
8, 5.0000, 4.329e-06, [ 0.3162 0.3162 -0.6316 -0.6333]
9, 5.0000, 6.927e-07, [ 0.3162 0.3162 -0.6321 -0.6328]
10, 5.0000, 1.108e-07, [ 0.3162 0.3162 -0.6323 -0.6326]
11, 5.0000, 1.773e-08, [ 0.3162 0.3162 -0.6324 -0.6325]
12, 5.0000, 2.837e-09, [ 0.3162 0.3162 -0.6324 -0.6325]
この場合,絶対値最大の固有値が求められていない.(しかし,$5$ 自体は $A$ の固有値である.)一方で,初期ベクトルを少しだけずらすと,以下のように反復回数は多くなるものの,絶対値最大の固有値が求められる.
In [10]:
init = np.array([1.1, 2, 3, -9]) # 初期ベクトル
tol = 1e-8 # 許容誤差
iteration, eval, increment, evec = power1(A, init, tol)
print("反復, 固有値, 増分, 固有ベクトル")
for i in range(iteration):
print(f"{i:d}, {eval[i]:.4f}, {increment[i]:.3e}, ",evec[i,:])
Out [10]:
反復, 固有値, 増分, 固有ベクトル
0, 2.7145, 1.000e+00, [ 0.1127 0.205 0.3075 -0.9224]
1, 3.9944, 3.204e-01, [ 0.2559 0.2866 -0.099 -0.9179]
2, 4.7891, 1.659e-01, [ 0.3323 0.3396 -0.3983 -0.7846]
3, 5.0169, 4.542e-02, [ 0.378 0.3794 -0.5124 -0.6713]
4, 5.2085, 3.679e-02, [ 0.4399 0.4402 -0.5212 -0.584 ]
5, 5.7604, 9.580e-02, [ 0.5379 0.5379 -0.447 -0.4707]
6, 7.0904, 1.876e-01, [ 0.6502 0.6502 -0.274 -0.2819]
7, 8.7094, 1.859e-01, [ 0.7054 0.7054 -0.0479 -0.05 ]
8, 9.5999, 9.276e-02, [0.6961 0.6961 0.1246 0.1242]
9, 9.8936, 2.968e-02, [0.6718 0.6718 0.2206 0.2205]
10, 9.9730, 7.959e-03, [0.654 0.654 0.2689 0.2689]
11, 9.9932, 2.026e-03, [0.6437 0.6437 0.2927 0.2927]
12, 9.9983, 5.089e-04, [0.6382 0.6382 0.3045 0.3045]
13, 9.9996, 1.274e-04, [0.6353 0.6353 0.3104 0.3104]
14, 9.9999, 3.185e-05, [0.6339 0.6339 0.3133 0.3133]
15, 10.0000, 7.963e-06, [0.6332 0.6332 0.3148 0.3148]
16, 10.0000, 1.991e-06, [0.6328 0.6328 0.3155 0.3155]
17, 10.0000, 4.977e-07, [0.6326 0.6326 0.3159 0.3159]
18, 10.0000, 1.244e-07, [0.6325 0.6325 0.316 0.316 ]
19, 10.0000, 3.111e-08, [0.6325 0.6325 0.3161 0.3161]
20, 10.0000, 7.777e-09, [0.6325 0.6325 0.3162 0.3162]
これらの現象を説明するために,冪乗法の収束に関して,次の結果を復習しよう.例えば,[齊藤2012]の定理5.2.1を見よ.
定理. $(\star)$を仮定する.さらに,$\|\boldsymbol{x}^{(0)}\|=1$ かつ $\boldsymbol{x}^{(0)}\not\in\mbox{span}~\{\boldsymbol{v}_1,\ldots,\boldsymbol{v}_{n-1}\}$ とする. このとき,$r=|\lambda_{n-1}/\lambda_n|(<1)$ とおくと, \begin{equation*} |\lambda_n-\mu^{(k)}|\le Cr^k\qquad (k\ge k_0) \end{equation*} を満たす定数 $C>0$ と $0 < k_0 \in\mathbb{Z}$ が存在する. また, \begin{equation*} \left\|\frac{\|A^k\boldsymbol{x}^{(0)}\|}{c_n\lambda_n^k}\boldsymbol{x}^{(k)}-\boldsymbol{v}_n\right\| \le C' r^k\qquad (k\ge k_0) \end{equation*} を満たす定数 $C ' >0$ が存在する.$\blacksquare$
あらためて,In [9]では,初期ベクトルを $\boldsymbol{x}^{(0)}=(1,2,3,-9)^{\scriptsize \mbox{T}}$ と選ぶと, 近似固有値として $\lambda_3=5$ が得られている. これは,$\langle \boldsymbol{v}_4,\boldsymbol{x}^{(0)}\rangle=0$,すなわち, $\boldsymbol{x}^{(0)}\in\operatorname{span}\{\boldsymbol{v}_1,\boldsymbol{v}_2,\boldsymbol{v}_3\}$ となっており,定理の仮定が満たされていないためであり,定理とは矛盾しない. 実際,In [10]では,$\boldsymbol{x}^{(0)}$ を少しだけずらして,$\boldsymbol{x}^{(0)}=(1.1,2,3,-9)^{\scriptsize \mbox{T}}$ とすることで,正しく $\lambda_4=10$ が得られている.
逆冪乗法
まず, \[ A\boldsymbol{v}_1=\lambda_1\boldsymbol{v}_1\quad\Leftrightarrow\quad A^{-1}\boldsymbol{v}_1=\lambda_1^{-1}\boldsymbol{v}_1 \] なので,$\lambda_1^{-1}$ は,$A^{-1}$ の絶対値最大の固有値となる. したがって,絶対値最小の固有値が唯一存在するならば,すなわち, $|\lambda_1|< |\lambda_i|$($i\ge 2$)ならば, $A^{-1}$ に冪乗法を適用することにより,$1/\lambda_1$ が得られる.
次に,$\alpha\in\mathbb{C}$ に対して, $B=A-\alpha I$ の固有値は $\mu_i=\lambda_i-\alpha$,対応する固有ベクトルは $\boldsymbol{v}_i$ となる.ここで, \begin{equation*} |\mu_k|<|\mu_i| \quad\Leftrightarrow\quad |\lambda_k-\alpha|<|\lambda_i-\alpha| \quad (i\ne k) \end{equation*} を満たす $\lambda_k$ の存在を仮定する.すなわち,$\lambda_k$ は $\alpha$ に最も近い $A$ の固有値である.このとき,$E=B^{-1}=(A-\alpha I)^{-1}$ とおくと, \[ \lambda_k=R_A(\boldsymbol{v}_k),\quad \mu_k=R_B(\boldsymbol{v}_k), \quad \mu_k^{-1}=R_E(\boldsymbol{v}_k) \] が成り立つことに注意せよ. $E$ に冪乗法を適用することで,$\boldsymbol{v}_k$ の近似値が得られるので, $\mu_k$ や $\lambda_k$ の近似値が計算できる.
逆冪乗法(逆反復法)のアルゴリズム
$\alpha\in\mathbb{C}$ の最も近くにある固有値 $\lambda$ を計算するために,反復列を次で生成する: \begin{equation*} \boldsymbol{y}^{(k)}=(A-\alpha I)^{-1}\boldsymbol{x}^{(k)},\quad \boldsymbol{x}^{(k+1)}=\frac{1}{\|\boldsymbol{y}^{(k)}\|}\boldsymbol{y}^{(k)} \quad (k=0,1,\ldots). \end{equation*} なお,$\boldsymbol{y}^{(k)}$は,連立一次方程式 \begin{equation*} (A-\alpha I)\boldsymbol{y}^{(k)}=\boldsymbol{x}^{(k)} \end{equation*} を解いて求める.このとき,$\boldsymbol{x}^{(k+1)}$ が近似固有ベクトルである.近似固有値 $\tilde{\lambda}$ は,次で得られる: \[ \tilde{\lambda}=R_A(\boldsymbol{x}^{(k+1)})=\frac{1}{R_E(\boldsymbol{x}^{(k+1)})}+\alpha. \] ただし,$E=(A-\alpha I)^{-1}$ とおいている.$\blacksquare$
In [11]:
def invpower1(A, initial, alpha, tolerance):
kmax = 100
eval = np.array([])
increment = np.array([])
evec = np.copy(init)
E = A - alpha * np.eye(A.shape[0])
k = 0
x = init / la.norm(init, ord=2)
muold = 0
inc = tolerance + 1
while k <= kmax and inc >= tolerance:
y = la.solve(E, x)
mu = np.vdot(x, y)
inc = np.abs((mu - muold) / mu)
eval = np.append(eval, 1/mu + alpha)
increment = np.append(increment, inc)
evec = np.vstack((evec, x))
x = y / la.norm(y, ord=2)
muold = mu
k += 1
return k, eval, increment, evec[1:, :]
まずは,絶対値最小の固有値を求めてみよう.
In [12]:
A=np.array([[5,4,1,1], [4,5,1,1],[1,1,4,2],[1,1,2,4]])
init = np.array([1, 0, 0, 0]) # 初期ベクトル
tol = 1e-8 # 許容誤差
iteration, eval, increment, evec = invpower1(A, init, 0, tol)
print("反復, 固有値, 増分, 固有ベクトル")
for i in range(iteration):
print(f"{i:d}, {eval[i]:.4f}, {increment[i]:.3e}, ",evec[i,:])
Out [12]:
反復, 固有値, 増分, 固有ベクトル
0, 1.7857, 1.000e+00, [1. 0. 0. 0.]
1, 1.0136, 4.324e-01, [ 0.78569895 -0.61733489 -0.02806068 -0.02806068]
2, 1.0003, 1.306e-02, [ 0.71827685 -0.69565396 -0.00848358 -0.00848358]
3, 1.0000, 3.169e-04, [ 0.70879902 -0.70540493 -0.00197989 -0.00197989]
4, 1.0000, 1.054e-05, [ 7.07389440e-01 -7.06823755e-01 -4.24263958e-04 -4.24263958e-04]
5, 1.0000, 4.003e-07, [ 7.07157686e-01 -7.07055862e-01 -8.76812400e-05 -8.76812400e-05]
6, 1.0000, 1.580e-08, [ 7.07116398e-01 -7.07097164e-01 -1.78190909e-05 -1.78190909e-05]
7, 1.0000, 6.299e-10, [ 7.07108648e-01 -7.07104914e-01 -3.59210245e-06 -3.59210245e-06]
$\alpha$ を変化させると,いろいろな固有値が求められる. ただし,初期ベクトルの取り方次第では,予期せぬ固有値を求めることがある.
In [13]:
init = np.array([1, 2, 3, 4]) # 初期ベクトル
tol = 1e-8 # 許容誤差
iteration, eval, increment, evec = invpower1(A, init, 3.0, tol)
print("反復, 固有値, 増分, 固有ベクトル")
for i in range(iteration):
print(f"{i:d}, {eval[i]:.4f}, {increment[i]:.3e}, ",evec[i,:])
Out [13]:
反復, 固有値, 増分, 固有ベクトル
0, 6.8889, 1.000e+00, [0.18257419 0.36514837 0.54772256 0.73029674]
1, 6.9978, 2.801e-02, [ 0.03573708 -0.21442251 0.89342711 0.39310793]
2, -6.4842, 3.372e+00, [-0.3049266 -0.08520008 0.06726322 0.94616931]
3, 1.2973, 8.205e-01, [-0.08075426 -0.23047701 0.93282079 -0.26496126]
4, 1.8494, 3.243e-01, [-0.13347429 -0.04913961 -0.48841052 0.86094429]
5, 1.9637, 9.928e-02, [-0.02597999 -0.06964021 0.79472391 -0.60240285]
6, 1.9910, 2.638e-02, [-0.03521592 -0.0131865 -0.65646127 0.7534219 ]
7, 1.9978, 6.702e-03, [-0.00661957 -0.01765963 0.73085397 -0.68227326]
8, 1.9994, 1.682e-03, [-0.0088365 -0.00331329 -0.69481949 0.71912225]
9, 1.9999, 4.210e-04, [-0.00165711 -0.00441911 0.71314925 -0.70099634]
10, 2.0000, 1.053e-04, [-0.00220967 -0.00082862 -0.70405997 0.7101366 ]
11, 2.0000, 2.632e-05, [-4.14317275e-04 -1.10484917e-03 7.08623828e-01 -7.05585486e-01]
12, 2.0000, 6.580e-06, [-5.52426492e-04 -2.07159769e-04 -7.06346663e-01 7.07865837e-01]
13, 2.0000, 1.645e-06, [-1.03580038e-04 -2.76213497e-04 7.07486442e-01 -7.06726855e-01]
14, 2.0000, 4.113e-07, [-1.38106781e-04 -5.17900396e-05 -7.06916851e-01 7.07296645e-01]
15, 2.0000, 1.028e-07, [-2.58950226e-05 -6.90533950e-05 7.07201721e-01 -7.07011824e-01]
16, 2.0000, 2.570e-08, [-3.45266981e-05 -1.29475117e-05 -7.07059305e-01 7.07154253e-01]
17, 2.0000, 6.426e-09, [-6.47375591e-06 -1.72633491e-05 7.07130518e-01 -7.07083044e-01]
In [14]:
init = np.array([1, 0, 1, 1]) # 初期ベクトル
tol = 1e-8 # 許容誤差
iteration, eval, increment, evec = invpower1(A, init, 2.1, tol)
print("反復, 固有値, 増分, 固有ベクトル")
for i in range(iteration):
print(f"{i:d}, {eval[i]:.4f}, {increment[i]:.3e}, ",evec[i,:])
Out [14]:
反復, 固有値, 増分, 固有ベクトル
0, 53.5306, 1.000e+00, [0.57735027 0. 0.57735027 0.57735027]
1, 0.4730, 1.032e+00, [-0.61817401 0.61226618 0.34856206 0.34856206]
2, 0.9411, 2.877e-01, [ 0.65551242 -0.73226355 0.13056331 0.13056331]
3, 0.9918, 4.375e-02, [-0.72525638 0.68516524 0.04770625 0.04770625]
4, 0.9988, 6.324e-03, [ 0.69848014 -0.71518802 0.01777065 0.01777065]
5, 0.9998, 9.107e-04, [-0.71033942 0.70379567 0.00669177 0.00669177]
6, 1.0000, 1.310e-04, [ 0.70584581 -0.70835647 0.00253127 0.00253127]
7, 1.0000, 1.885e-05, [-0.70758411 0.70662783 0.00095915 0.00095915]
8, 1.0000, 2.713e-06, [ 7.06925024e-01 -7.07288304e-01 3.63681013e-04 3.63678508e-04]
9, 1.0000, 3.903e-07, [-7.07175701e-01 7.07037828e-01 1.37914549e-04 1.37942104e-04]
10, 1.0000, 5.615e-08, [ 7.07080625e-01 -7.07132932e-01 5.24665250e-05 5.21634158e-05]
11, 1.0000, 8.134e-09, [-7.07116702e-01 7.07096860e-01 1.81761365e-05 2.15103385e-05]
In [15]:
init = np.array([1, 0, 0, 0]) # 初期ベクトル
tol = 1e-8 # 許容誤差
iteration, eval, increment, evec = invpower1(A, init, 5.7, tol)
print("反復, 固有値, 増分, 固有ベクトル")
for i in range(iteration):
print(f"{i:d}, {eval[i]:.4f}, {increment[i]:.3e}, ",evec[i,:])
Out [15]:
反復, 固有値, 増分, 固有ベクトル
0, -0.7014, 1.000e+00, [1. 0. 0. 0.]
1, 4.8475, 8.668e-01, [-0.31347013 0.11347335 0.66665594 0.66665594]
2, 4.9962, 1.745e-01, [ 0.38381183 0.31385033 -0.61407917 -0.61407917]
3, 4.9999, 5.200e-03, [-0.31597406 -0.30552752 0.63514303 0.63514303]
4, 5.0000, 1.297e-04, [ 0.31789358 0.31633762 -0.63201036 -0.63201036]
5, 5.0000, 3.241e-06, [-0.31619901 -0.31596727 0.63252781 0.63252781]
6, 5.0000, 8.153e-08, [ 0.31626856 0.31623405 -0.63244376 -0.63244376]
7, 5.0000, 2.064e-09, [-0.3162265 -0.31622136 0.63245745 0.63245745]
Gershgorinの定理
逆冪乗法を利用するにあたり,固有値の存在範囲についての情報があると便利である.
定理(Gershgorinの定理). $A=(a_{i,j})\in\mathbb{C}^{n\times n}$ のすべての固有値は $\displaystyle{G=\bigcup_{i=1}^nG_{i}}$ の中に含まれる. ただし,$G_i =\{z\in\mathbb{C}\mid |z-a_{i,i}|\le r_i\}$,かつ, $\displaystyle{r_i=\sum_{1\le j\le n,j\ne i}|a_{i,j}|}$ である.各 $G_i$ のことをGershgorinの円盤と呼ぶ.$\blacksquare$
In [16]:
def gershgorin(A):
n = len(A)
centers = np.diag(A)
radii = np.sum(np.abs(A - np.diag(centers)), axis=1)
bounds = np.array([centers.real - radii, centers.real + radii, centers.imag - radii, centers.imag + radii])
fig, ax = plt.subplots()
ax.set_aspect('equal')
for center, radius in zip(centers, radii):
circle = plt.Circle((center.real, center.imag), radius, color='b', fill=False)
ax.add_artist(circle)
print(f"実部の範囲: {bounds[0].min():.2f}, {bounds[1].max():.2f}")
print(f"虚部の範囲: {bounds[2].min():.2f}, {bounds[3].max():.2f}")
plt.xlim(bounds[0].min(), bounds[1].max())
plt.ylim(bounds[2].min(), bounds[3].max())
ax.set_xlabel('Real')
ax.set_ylabel('Imaginary')
ax.grid(True)
plt.show()
In [17]: A = np.array([[5,4,1,1], [4,5,1,1],[1,1,4,2],[1,1,2,4]]) gershgorin(A) Out [17]: 実部の範囲: -1.00, 11.00 虚部の範囲: -6.00, 6.00
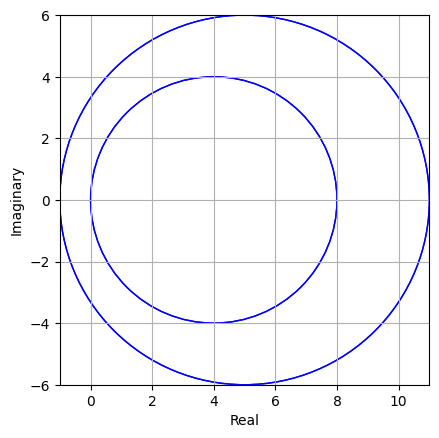
$A$ についてGershgorinの円盤を計算してみると,Out [17]と図5.1のようになる.これより,絶対値最大の固有値について $|\lambda_4|\le 11$ という評価が得られるので, この情報を利用して,$\alpha=11$ と選んで,逆冪乗法を適用するとOut [18]のようになる.
Out [4]と比較すると,単純に冪乗法を適用するよりも,少ない反復回数で,近似固有値が得られていることがわかる.ただし,冪乗法では一回の反復で行列とベクトルの積を計算するのみであるが,逆冪乗法では連立一次方程式を計算しなければならないので,反復回数のみでは,計算の手間の比較はできない.
In [18]:
A=np.array([[5,4,1,1], [4,5,1,1],[1,1,4,2],[1,1,2,4]])
init = np.array([1, 0, 0, 0]) # 初期ベクトル
tol = 1e-8 # 許容誤差
iteration, eval, increment, evec = invpower1(A, init, 11, tol)
print("反復, 固有値, 増分, 固有ベクトル")
for i in range(iteration):
print(f"{i:d}, {eval[i]:.4f}, {increment[i]:.3e}, ",evec[i,:])
Out [18]:
反復, 固有値, 増分, 固有ベクトル
0, 8.8571, 1.000e+00, [1. 0. 0. 0.]
1, 9.9830, 5.254e-01, [-0.73079405 -0.57419533 -0.26099788 -0.26099788]
2, 9.9997, 1.644e-02, [0.64465082 0.62884194 0.3073948 0.3073948 ]
3, 10.0000, 2.676e-04, [-0.63397602 -0.63239488 -0.31476271 -0.31476271]
4, 10.0000, 5.455e-06, [0.63265654 0.63249843 0.31598374 0.31598374]
5, 10.0000, 1.317e-07, [-0.63248377 -0.63246796 -0.3161871 -0.3161871 ]
6, 10.0000, 3.461e-09, [0.63245971 0.63245813 0.31622099 0.31622099]
QR分解
$A\in\mathbb{R}^{n\times n}$ を,直交行列 $Q$ と上三角行列 $R$ を用いて, \begin{equation*} A=QR ,\quad Q^{\scriptsize\mbox{T}}Q=QQ^{\scriptsize\mbox{T}}=I, \quad R= \begin{pmatrix} r_{1,1} & \cdots & r_{1,n}\\ % & r_{2,2} & & \vdots \\ & \ddots & \vdots \\ {\Large 0} & & r_{n,n}\\ \end{pmatrix} \end{equation*} の形に書くことを,QR分解と呼ぶ.このような分解が得られていれば, 連立一次方程式 $A\boldsymbol{x}=\boldsymbol{b}$ は, \begin{equation*} QR\boldsymbol{x}=\boldsymbol{b} \quad \Leftrightarrow \quad \begin{cases} R\boldsymbol{x}=\boldsymbol{c} &\\ Q\boldsymbol{c}=\boldsymbol{b} & \end{cases} \end{equation*} と同値であるから,はじめに $\boldsymbol{c}=Q^{-1}\boldsymbol{b}=Q^{\scriptsize\mbox{T}} \boldsymbol{b}$ で $\boldsymbol{c}$ を求めて おいて,後は $R\boldsymbol{x}=\boldsymbol{c}$ にしたがって, $\boldsymbol{x}$ を計算することができる.
任意の正則行列$A\in\mathbb{R}^{n\times n}$は,グラム・シュミットの直交化法によりQR分解が可能である.QR分解の一意性を述べるために, \begin{equation} S= \begin{pmatrix} s_{1} & & {\Large 0}\\ & \ddots & \\ {\Large 0} & & s_{n}\\ \end{pmatrix}\in\mathbb{R}^{n\times n},\qquad s_i^2=1\quad (i=1,\ldots,n) \label{eq:l.6.55} \end{equation} を満たす対角行列を考える.このような形の行列を,符号行列と呼ぶ. 正則行列$A\in\mathbb{R}^{n\times n}$ が,$A=Q_1R_1$,$A=Q_2R_2$ と二通りにQR分解できたとすると,$Q_1=SQ_2$,$R_1=R_2S$ を満たす符号行列 $S\in\mathbb{R}^{n\times n}$ が存在する.
詳しくは,[齊藤2012]の2.7節を見よ.
QR法
$A\in\mathbb{R}^{n\times n}$のすべての固有値を,反復的にかつ同時的に計算する方法であるQR法について述べる.そのために,$A$ が,相異なる $n$ 個の実固有値 $\lambda_1,\ldots,\lambda_n$ を持つと仮定する.このとき,$A$ は適当な直交行列 $U$ により,\begin{equation} U^{\scriptsize\mbox{T}} AU= \begin{pmatrix} b_{1,1} & \cdots & b_{1,n}\\ % & b_{2,2} & & \vdots \\ & \ddots & \vdots \\ {\Large 0} & & b_{n,n}\\ \end{pmatrix} =B ,\qquad b_{i,i}=\lambda_i\quad (1\le i\le n) \label{eq:e.3.0} \end{equation} と表現できる.これは,Schur分解の実行列版である.例えば,[齊藤2012]の命題2.8.1と注意2.8.4を見よ.
したがって,このような $U$ を求めることができれば,すべての固有値が同時に求まることになるが,もちろんそれは難しい.そこで,$U$ に十分近い行列 $\tilde{Q}$ を作って,$\tilde{Q}^{\scriptsize\mbox{T}} A\tilde{Q}$ を計算すれば,この対角成分が求めたい $A$ の固有値の近似値であろうことが期待できる.もう少し具体的には,「何らかの基準」で直交行列の列 $\{Q_1,Q_2,\ldots,\}$ を作って,$A_1=A$, \begin{equation} A_{k+1}=Q_k^{\scriptsize\mbox{T}} A_{k}Q_k= Q_k^{\scriptsize\mbox{T}} Q_{k-1}^{\scriptsize\mbox{T}} \cdots Q_1^{\scriptsize\mbox{T}} A \underbrace{Q_1 \cdots Q_{k-1}Q_k}_{=\tilde{Q}_k}=\tilde{Q}_k^{\scriptsize\mbox{T}} A\tilde{Q}_k \end{equation} とする.明らかに,$\tilde{Q}_k$ は直交行列である.「何らかの基準」は,当然,$k\to\infty$ の際, $\tilde{Q}_k\to U$,$A_k\to B$ となるように設定しなければならない. そして,十分大きな $k$ をとり,$A_k$ の対角成分を$\lambda_1,\ldots,\lambda_n$ の近似値として採用するわけである.
QR法は,その名前から想像できるように,QR分解を応用して直交行列の列 $\{Q_1,Q_2,\ldots,\}$ を生成する.具体的には,
- $A_1=A$とする.
- $k=1,2,\ldots$ に対して,$A_k$ を $A_k=Q_kR_k$($Q_k$ は直交行列, $R_k$ は上三角行列)とQR分解し, \begin{equation*} A_{k+1}=R_kQ_k \end{equation*} と更新する.
QR法の収束については,例えば,[齊藤2012]の5.3節を見よ.
実際にQR法を実行してみよう.本来ならば,(教育的な配慮からは) QR分解の部分も自作するのが望ましいが,今回は, numpyの linalgの関数を利用する.
In [19]:
A=np.array([[5,4,1,1], [4,5,1,1],[1,1,4,2],[1,1,2,4]])
Q,R = la.qr(A)
print("Q=\n",Q)
print("Q*Q.T=\n",Q@Q.T)
print("R=\n",R)
Out [19]:
=
[[-0.76249285 0.62855011 0.14391842 -0.05307449]
[-0.60999428 -0.77741724 0.14391842 -0.05307449]
[-0.15249857 -0.01654079 -0.89229418 -0.42459591]
[-0.15249857 -0.01654079 -0.40297156 0.90226632]]
Q*Q.T=
[[ 1.00000000e+00 -4.25533324e-17 5.10976254e-17 -1.62255567e-17]
[-4.25533324e-17 1.00000000e+00 3.84593793e-17 -1.53901357e-17]
[ 5.10976254e-17 3.84593793e-17 1.00000000e+00 -1.17695776e-16]
[-1.62255567e-17 -1.53901357e-17 -1.17695776e-16 1.00000000e+00]]
R=
[[-6.55743852 -6.40493995 -2.28747855 -2.28747855]
[ 0. -1.40596735 -0.24811189 -0.24811189]
[ 0. 0. -4.087283 -3.10863778]
[ 0. 0. 0. 2.65372446]]
これを用いれば,QR法の計算は次のように実行できる.
In [20]:
def qr_method(A, tol):
kmax = 100
Ak = np.copy(A)
eval = np.diag(Ak)
for k in range(kmax):
Q, R = la.qr(Ak)
Ak = R@Q
eval = np.vstack((eval, np.diag(Ak)))
if np.abs(np.diag(Ak) - np.diag(A)).max() < tol:
break
A = np.copy(Ak)
return k, eval
In [21]:
A=np.array([[5,4,1,1], [4,5,1,1],[1,1,4,2],[1,1,2,4]])
tol=1e-9
iteration, eval = qr_method(A, tol)
print("反復, 固有値")
for i in range(iteration):
print(f"{i:d}, ",eval[i,:])
Out [22]:
反復, 固有値
0, [5. 5. 4. 4.]
1, [9.60465116 1.10123119 4.89975145 2.3943662 ]
2, [9.92197883 1.00109809 5.01422715 2.06269592]
3, [9.98053357 1.00001118 5.00955502 2.00990023]
4, [9.99512184 1.00000011 5.00330192 2.00157613]
5, [9.99877959 1. 5.0009686 2.0002518 ]
6, [9.99969484 1. 5.00026489 2.00004027]
7, [9.99992371 1. 5.00006985 2.00000644]
8, [9.99998093 1. 5.00001804 2.00000103]
9, [9.99999523 1. 5.0000046 2.00000016]
10, [9.99999881 1. 5.00000117 2.00000003]
11, [9.9999997 1. 5.00000029 2. ]
12, [9.99999993 1. 5.00000007 2. ]
13, [9.99999998 1. 5.00000002 2. ]
14, [10. 1. 5. 2.]
問題
- 上記の入力と出力をすべて確かめよ.
- 行列 $A$ やパラメータ値を変えて,計算を再試行せよ.
- 例題を自分で設定して,上記の方法を試せ.
課題
以下の課題は,冪乗法か逆冪乗法の利用を想定している.
課題5.1
2つの行列 \[ A_+= \begin{pmatrix} 30 & 2 & 3 & 13 \\ 5 & 11 & 10 & 8\\ 9 & 7 & 6 &12 \\ 4 & 14 & 15 & 1 \end{pmatrix} ,\quad A_-= \begin{pmatrix} -30 & 2 & 3 & 13 \\ 5 & 11 & 10 & 8\\ 9 & 7 & 6 &12 \\ 4 & 14 & 15 & 1 \end{pmatrix} \] を考える第 $(1,1)$ 成分以外の成分は全て等しいことに注意せよ.$A_{+}$ の絶対値最大の固有値と固有ベクトルを冪乗法を使って求めよ. 次に,$A_{-}$ の絶対値最大の固有値と固有ベクトルを冪乗法を使って求め,$A_{+}$ の場合との収束の速さの違いについて考察せよ.
課題5.2
行列 \[ A= \begin{pmatrix} 3 & 1 & 0 & 0 & 0 & 0 & 0 \\ 1 & 2 & 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 1 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 1 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 & 2 & 1 \\ 0 & 0 & 0 & 0 & 0 & 1 & 3 \\ \end{pmatrix} \] の最大固有値と絶対値が最大になる負の固有値を求めよ. 特に,絶対値最大の固有値を求めるために冪乗法を適用すると,どのような結果になるかを報告せよ.
課題5.3
行列 \[ A= \begin{pmatrix} 0 & 0 & 0 & -26 \\ 1 & 0 & 0 & 51\\ 0 & 1 & 0 &-33 \\ 0 & 0 & 1 & 9 \end{pmatrix} \] の絶対値最小の固有値を逆冪乗法で求めよ.また, 絶対値最大の固有値を求めるために冪乗法を適用すると,どのような結果になるかを報告せよ.
参考文献
- [齊藤2012] 齊藤宣一,数値解析入門,東京大学出版会,2012年
- [Quarteroni2014] A. Quarteroni, F. Saleri, P. Gervasio, Scientific Computing with MATLAB and Octave (4th edition), Springer, 2014(加古孝,千葉文浩訳,MATLABとOctaveによる科学技術計算,丸善出版,2014年)
固有値問題の具体的な応用例については[Quarteroni2014]の6.1節を見よ. 画像圧縮や都市間の鉄道ネットワークへの応用例が述べられている.