2024-3S 計算数理演習(東京大学理学部・教養学部) [齊藤宣一] [top] [0] [1] [2] [3] [4] [5] [6] [7] [8] [UTOL]
6. 常微分方程式の初期値問題(基礎編)
この節では,常微分方程式の初期値問題に対する数値的解法の基本事項を述べる.感染症の数理モデルなどへの具体的な応用は,次節で扱う.
なお,本節で説明する計算手法は,scipyモジュールの scipy.integrate.odeint や scipy.integrate.solve_ivp などにより,ブラックボックス的に利用できてしまう.しかし,本講義の目標は,数値解法の数理を習得することにあるので,このようなモジュールはあえて使わない.
もちろん,この講義の後に,自身の研究の中では,scipy.integrate.odeint や scipy.integrate.solve_ivp などを,有効活用することを勧める.
Euler法
常微分方程式の初期値問題 \begin{equation} \tag{6.1} \frac{du(t)}{dt}=f(t,u(t))\quad (t_0 < t < T),\quad u(t_0)=a \end{equation} を考える.なお,$f(t,y)$ は,少なくとも,$t$ についても,$y$ についても連続な関数としておく. (6.1)の解 $u(t)$ が,$t_0\le t\le T$ で一意的に存在することを保証するためには,$f$ について,さらに仮定をおく必要があるが,この段階では,この点について深く追求しない.
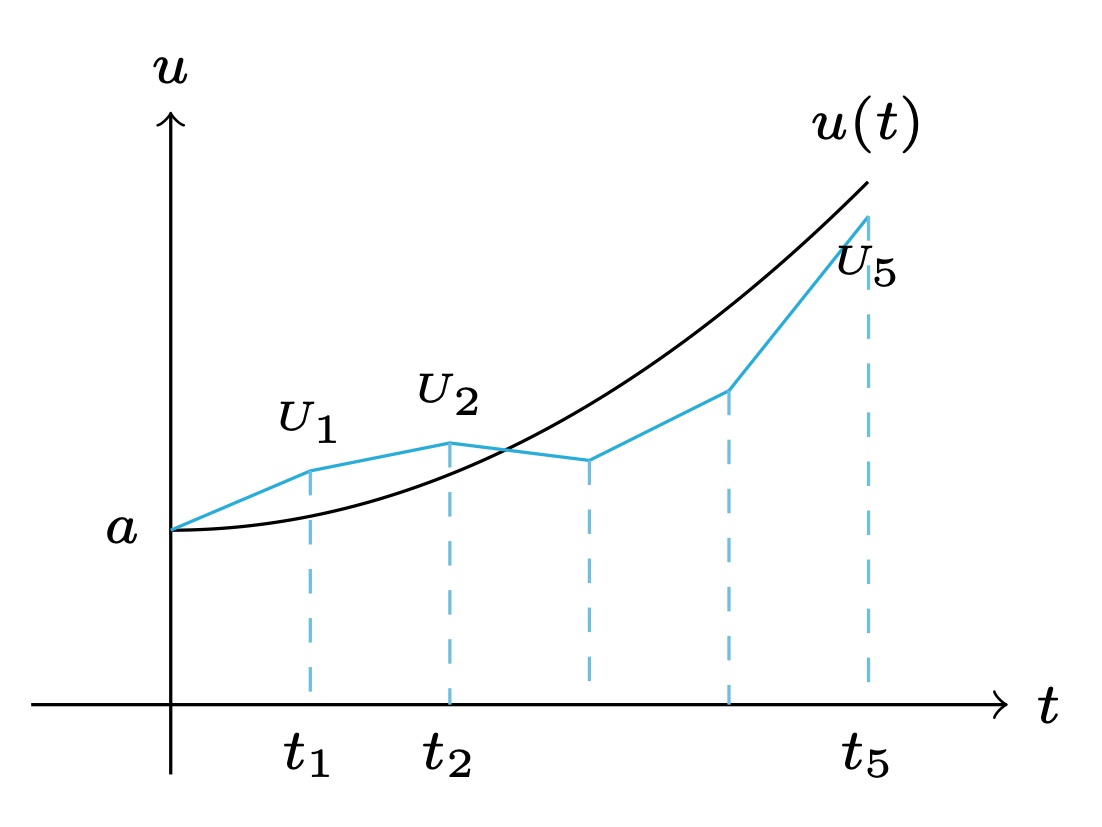
正の整数 $N$ に対して, $\displaystyle{ h=\frac{T-t_0}{N}}$ とおき(一様刻み幅), $t_n=t_0+nh$ $(n=0,\ldots,N)$ と定義して,$U_n\approx u(t_n)$ を求めることを考える. Euler法(前進Euler法)とは, \begin{equation*} \frac{U_{n+1}-U_n}{h}=f(t_n,U_n), \end{equation*} すなわち, \begin{equation} \tag{6.2} U_{n+1}=U_n+hf(t_n,U_n)\quad (n=0,\ldots,N-1) \end{equation} で $U_n$ を求める方法である.ただし,$U_0=a$ とする.
例6.1
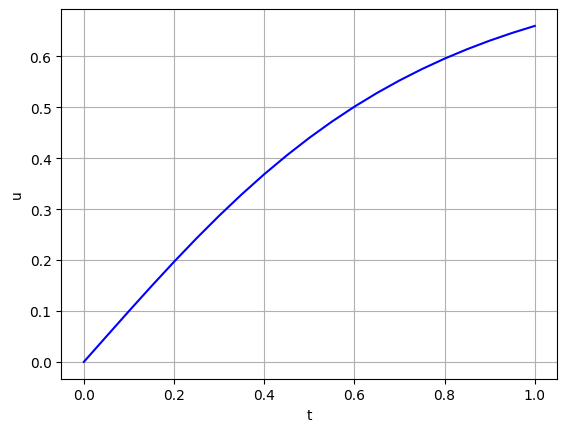
常微分方程式の初期値問題 \begin{equation*} \frac{du(t)}{dt}=\cos (2u(t))\quad (t_0=0 < t < T),\quad u(0)=0 \end{equation*} の解は $\displaystyle{u(t)=\frac12 \sin^{-1}\left( \frac{e^{4t}-1}{e^{4t}+1}\right)}$ である.$\blacksquare$
In [1]: import numpy as np import matplotlib.pyplot as plt
In [2]:
def euler(odefunc, t0, T, initial, N):
t=np.linspace(t0, T, N+1)
u=np.zeros(t.shape)
h=(T-t0)/N
u[0]=initial
for n in range (N):
u[n+1] = u[n] + h*odefunc(t[n],u[n])
return h, t, u
In [3]:
#右辺の関数
def func1(t, y):
return np.cos(2*y)
N=20
t0=0.0
T=1.0
u0=0
h, t, u = euler(func1, t0, T, u0, N)
plt.plot(t, u,'b')
plt.xlabel('t')
plt.ylabel('u')
plt.grid('on')
plt.show()
Euler法による近似解 $U_n$ と,微分方程式の解 $u(t_n)$ との誤差 \begin{equation*} E_n=U_n-u(t_n)\qquad (n=0,1,\ldots,N) \end{equation*} を考察しよう. まず, \begin{align} \frac{E_{n+1}-E_n}{h} &= \frac{U_{n+1}-U_n}{h}-\frac{u(t_{n}+h)-u(t_n)}{h} \nonumber \\ &=f(t_n,U_n)-\frac{u(t_{n+1})-u(t_n)}{h} \label{eq:o.1.17} \end{align} となる.
天下り的であるが, \begin{equation*} \delta(t_n,h)\stackrel{\textrm{def.}}{=} \frac{u(t_{n+1})-u(t_n)}{h}-f(t_n,u(t_n)) \end{equation*} とおき,これをEuler法の局所離散化誤差(local truncation error, local discretization error) と言う. これらを使うと, \[ \frac{E_{n+1}-E_n}{h} =f(t_n,U_n)-f(t_n,u(t_n))-\delta(t_n,h) \] となり,誤差 $E_n$ の満たす方程式が導けた.一方で,$E_0=0$ は明らかである.
さて,$u(t)$ が十分に滑らかなら(具体的な仮定は,後の定理で述べる),Taylorの定理により, \begin{equation*} \exists \theta\in [0,1],\quad u(t_{n+1})=u(t_n+h)=u(t_n) +h\frac{du}{dt}(t_n) +\frac{h^2}{2}\frac{d^2u}{dt^2}(t_n+\theta h) \end{equation*} が成り立つ.これと,さらに,(6.1)を使うと, \begin{equation*} \delta(t_n,h)=\frac{h}{2}\frac{d^2u}{dt^2}(t_n+\theta h) \end{equation*} と書けるので, \begin{equation*} \max_{0\le n\le N-1}|\delta(t_n,h)|\le hM_2\qquad \left(M_2=\frac{1}{2}\max_{t_0\le t\le T}\left|\frac{d^2u(t)}{dt^2}\right|\right) \end{equation*} と評価できる.
一方で,$f(t,y)$ については,($t$ については一様に)Lipschitz連続性を仮定する: \begin{equation} \exists \lambda>0,\quad |f(t,y)-f(t,z)|\le \lambda |y-z| \qquad (t\in [t_0,T],~y,z\in\mathbb{R}). \tag{6.3} \end{equation}
以上の準備のもとで,次のように評価する.$1\le n\le N$ に対して, \begin{align*} |E_{n}| &= |E_{n-1} +h[f(t_{n-1},u(t_{n-1}))-f(t_{n-1},U_{n-1})]+h\delta (t_{n-1},h)|\\ &\le |E_{n-1}|+h\cdot \lambda\cdot |u(t_{n-1})-U_{n-1}| +h|\delta(t_{n-1},h)|\\ &\le (1+h\lambda)|E_{n-1}|+h\cdot hM_2\qquad (k=1+h\lambda\mbox{ とおく})\\ &\le k^2|E_{n-2}|+(k+1)h\cdot hM_2\le\cdots \\ &\le k^{n}|E_0|+(k^{n-1}+\cdots +k+1) h\cdot hM_2\\ &=\frac{k^{n}-1}{k-1} h\cdot hM_2. \end{align*} したがって, \begin{equation*} |E_n|\le \frac{k^n-1}{\lambda h}h\cdot hM_2\le \frac{e^{n\cdot \lambda h}-1}{\lambda}hM_2 \le \frac{e^{\lambda T}-1}{\lambda}M_2h \end{equation*} となることがわかる.この最右辺の項は,$n$ には依存しない.ここまでの考察 をまとめると,次の定理が証明できたことになる.
定理1. $u(t)$ $(t_0\le t\le T)$ を初期値問題(6.1)の解,$\{U_n\}_{n=0}^N$ をEuler法(6.2)の解とする. このとき,連続関数 $f(t,y)$ が,(6.3)を満たし,さらに,$u(t)$ が $C^2$ 級ならば, \begin{equation} \tag{6.4} \max_{0\le n\le N}|u(t_n)-U_n|\le \frac{e^{\lambda T}-1}{\lambda}M_2 h \end{equation} が成り立つ.$\blacksquare$
注意. (6.3)は,大域的なLipschitz連続性であり,実際のところ,応用上は現実的とは言えない.応用上妥当な問題に対して適用できるようにするために, 適当な正数 $M$ に対して,次の成立を仮定することが多い:
- $f(t,y)$ は,有界閉集合 \[ D_{T,M}=\{(t,y)\mid t_0\le t\le T,~|y-a|\le M\} \] 上の連続関数である.
- $f(t,y)$ は,($t$ に関して一様に)$y$ について$|y-a|\le M$ でリプシッツ連続,すなわち, \begin{equation*} |f(t,y)-f(t,z)|\le \lambda |y-z| \quad \left( \begin{array}{c} t\in [t_0,T]\\ |y-a|,\ |z-a|\le M \end{array} \right) \end{equation*} を満たす正定数 $\lambda$ が存在する($\lambda$ は $M$ に応じて定まる).
上の定理を実験的に確かめてみよう.そのために,誤差を, \[ \mathcal{E}_h\stackrel{\textrm{def.}}{=} \max_{0\le n\le N}|u(t_n)-U_n| \] とおき,前節(4. 数値積分)と同様に考察する. すなわち,$N_0=4$,$N_k=2^kN_0$,$h_k=(T-t_0)/N_k$ と定めて, \[ r_k=\frac{\log \mathcal{E}_{h_{k}}-\log \mathcal{E}_{h_{k+1}}}{\log h_{k}- \log h_{k+1}}\qquad (k=0,1,\ldots,7) \] と定義して,この量を観察する.
In [4]:
def OderError(Solver, odefunc, odeexact, t0, T, initial):
NN=4
kmax=8
hv=np.zeros(kmax)
ev=np.zeros(kmax)
for k in range(kmax):
h, t, u = Solver(odefunc, t0, T, initial, NN)
exact=np.vectorize(odeexact)(t)
error=u-exact
ev[k] = np.linalg.norm(error,ord=np.inf)
hv[k] = h
NN = 2*NN
rate=(np.log(ev[1:]) - np.log(ev[:-1])) / (np.log(hv[1:]) - np.log(hv[:-1]))
return hv, ev, rate
In [5]:
#右辺の関数
def func1(t, y):
return np.cos(2*y)
#厳密解
def exact1(t):
return 0.5*np.arcsin( (np.exp(4*t)-1) / (np.exp(4*t)+1) )
t0=0.0
T=1.0
u0=0
#
hv, ev, rate = OderError(euler, func1, exact1, t0, T, u0)
#収束の速さの出力
for i in range(rate.shape[0]-1):
print(f'{hv[i+1]:.3f}, {rate[i]:.3f}')
#結果の描画(両対数目盛)
plt.plot(hv, ev, 'bo-')
plt.xscale('log')
plt.yscale('log')
plt.legend(['Euler'])
plt.xlabel('h')
plt.ylabel('error')
plt.grid('on')
plt.gca().set_aspect('equal', adjustable='box')
plt.show()
Out [5]:
0.125, 1.084
0.062, 1.035
0.031, 1.019
0.016, 1.009
0.008, 1.005
0.004, 1.002
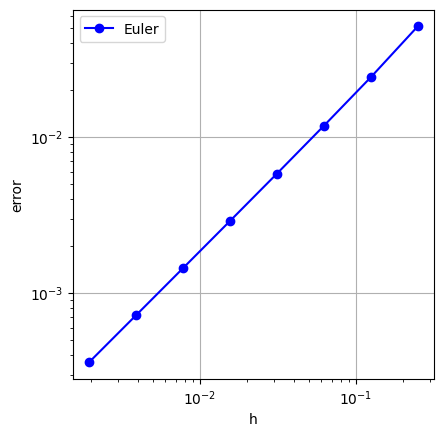
これで,少なくとも,例6.1の関数に対しては,Euler法の誤差は,$\mathcal{E}_h\approx Ch$ となることが実験的に確かめられた.
注意. $t_{n-1}$まで誤差が混入してない,すなわち, $u(t_k)=U_{k}$ $(k=1,\ldots,n-1)$ を仮定すると, $|E_n|\le h^2 M_2$ と評価できるので,$h$ が十分小さければ,$E_n=\pm M_2h^2+O(h^3)$ という関係があると考えられる.これを,Euler法は,局所的には2次精度である,という.一方で, (6.4)により,Euler法は,大域的には1次精度である,という.
Runge--Kutta法
次に,Euler法を一般化して, \begin{equation} \tag{6.5} U_{n+1}=U_n+hF(t_n,U_n,h)\quad (n=0,1,\ldots,N-1),\qquad U_0=a \end{equation} の形の近似解法を考えよう.$F(t,y,h)$ は,$t_0\le t\le T$, $y\in\mathbb{R}$,$h > 0$ に対して定義されている連続関数であり,近似解法がEuler法よりも優れたものになるようにその具体的な形を決めたい.
前節での考察を参考に,(6.5)の局所離散化誤差を \[ \delta(t_n,h)=\frac{u(t_h+h)-u(t_n)}{h}-F(t_n,u(t_n),h)\quad (n=0,\ldots,N-1) \] で定義する.ここで,$u(t)$ は初期値問題(6.1) の解である.さらに,前節における $hM_2$ の役割を果たすものと して, \[ \tau(h)=\max_{0\le n\le N-1}|\delta(t_n,h)| \] とおき,これを(6.5)の 大域離散化誤差(global truncation error, global discretization error)と呼ぶ.
さらに,$F(t,y,h)$ が,$y$ について,Lipschitz係数 $L > 0$ のLipschitz連続関数で あることを仮定する.すなわち, \begin{equation} \tag{6.6} |F(t,y,h)-F(t,z,h)|\le L |y-z| \qquad \left(\begin{array}{c} t\in [t_0,T]\\ y,z\in\mathbb{R},~h > 0 \end{array}\right) \end{equation} を仮定する.そうすると,前節と同様に計算することにより,近似解法(6.5)の誤差 $u(t_n)-U_n$ が, \begin{equation*} \max_{0\le n\le N}|u(t_n)-U_n|\le \frac{e^{L T}-1}{L}\tau(h) \end{equation*} を満たすことが導ける.
したがって,次の概念を導入するのが自然であろう.
定義. 近似解法(6.5)が初期値問題(6.1)と適合的(整合的)であるとは, \[ \lim_{h\to 0}\tau(h)= 0 \] が成り立つときを言う.一方で,$p\ge 1$ に対して, $p$ 次精度の公式であるとは, \begin{equation*} \tau(h)\le Ch^p \quad \end{equation*} を満たすような正定数 $C$ が存在するときを言う.ただし,(6.1)の解 $u(t)$ は十分に滑らかであると仮定している.$\blacksquare$
Euler法は,1次精度の公式である.まとめると,次の定理が証明できたことになる.
定理2. $u(t)$ を初期値問題(6.1)の解, $\{U_n\}_{n=0}^N$ を近似解法(6.5)の解とする. このとき,連続関数 $F(t,y,h)$ が,(6.6)を満たし,さらに, (6.5)が $p(\ge 1)$ 次精度の公式であるならば, \begin{equation*} \max_{0\le n\le N}|u(t_n)-U_n|\le C\frac{e^{L T}-1}{L}h^p \end{equation*} が成り立つ.$\blacksquare$
以上の考察を元に,$F(t,y,h)$ を具体的に決定しよう.そのために, \begin{equation} \tag{6.7a} U_{n+1}=U_n+ h(a k_1+bk_2) \end{equation} の形を仮定する.ただし,$k_1$ と $k_2$ は, \begin{equation} \tag{6.7b} k_1=f(t_n,U_n) ,\quad k_2=f(t_n+\alpha h,U_n+\beta h k_1) \end{equation} とする.ここに登場する $a,b,\alpha,\beta$ は,これから定める定数である. この公式では,$F(t,y,h)$ を \begin{equation*} F(t,y,h)= af(t,y)+bf(t+\alpha h,y+\beta hf(t,y)) \end{equation*} と選んでいることになる.
まず, $f(t,y)$ が,(6.3)を満たすならば, $F(t,y,h)$ は,Lipschitz係数$L=|a| \lambda + |b| \lambda (1 +\lambda|\beta|)$のLipschitz連続関数となる.
次に,なるべく大きな $p$ に対して,$\tau(h)\le Ch^p$ となるよう に,係数 $a,b,\alpha,\beta$ を決めたい. そのために,局所離散化誤差 $\delta(t_n,h)$ を計算する.詳細は省略するが(たとえば,[齊藤2017]の4.2節を見よ), $\alpha\ne 0$ を自由に設定するパラメータとして, \begin{equation*} a=1-\frac{1}{2\alpha},\quad b=\frac{1}{2\alpha},\quad \beta=\alpha \end{equation*} と選ぶと, \begin{equation*} \delta(t_n,h) = h^2 \underbrace{\left\{\left(\frac16-\frac{\alpha}{4}\right) (f_{tt}+f_{yy}f^2+2ff_{ty}) +\frac16(f_tf_y+ff_y^2)\right\}}_{=K}+Rh^3 \end{equation*} が導ける. ただし,$f_{ty}=(\partial^2f/\partial y\partial t)(t,u(t))$ などであり, $R$ には,$f_{ttt}$ や $d^4u/dt^4$などが含まれる.$K$ と $R$ は,$t$ と $u(t)$ に依存している.したがって,$u(t)$ や $f(t,y)$ が適当に滑らかなら, \[ |K|\le C_1,\quad |R|\le C_2\quad (t_0\le t\le T) \] を満たす正定数 $C_1$ と $C_2$ がとれるので,(6.7a,b)からなる近似解法について,その大域離散化誤差は, \[ \tau(h)\le C_1h^2+C_2h^3 \] を満たす.なお,$\alpha$ の値は $0$ 以外の任意の値を利用することができるが, 一般の $f(t,y)$ に対して,$K=0$ となるように $\alpha$ を選ぶことはできない.したがって,$\tau(h)\le C_2h^3$ となるように $\alpha$ を選ぶことはできない.すなわち,(6.7a,b)からなる近似解法は,2次精度であり,3次精度にはなり得ない.
このようなパラメータの選び方に基づいた近似解法(6.7a,b)を,2段数2次精度のRunge--Kutta法と言う.2段数の2は,公式を構成する $k_i$ の個数が2個であることを意味している.
例6.2 (2次精度のRunge--Kutta法の例)
$\alpha=1$ と選んだとき,すなわち, \begin{equation*} \begin{array}{rcl} U_{n+1}&=&U_n+\frac{h}{2}(k_1+k_2),\\ k_1&=&f(t_n,U_n),\\ k_2&=&f\left(t_n+h,U_n+hk_1\right) \end{array} \end{equation*} をHeun法と呼ぶ. 一方で,$\alpha=1/2$ と選んだとき, \begin{equation*} \begin{array}{rcl} U_{n+1}&=&U_n+hk_2,\\ k_1&=&f(t_n,U_n),\\ k_2&=&f\left(t_n+\mbox{$\frac12$}h,U_n+\mbox{$\frac12$}hk_1\right) \end{array} \end{equation*} を改良Euler法と呼ぶ. もちろん,これらは,2段数2次精度である.$\blacksquare$
Heun法を試してみよう.
In [6]:
def heun(odefunc, t0, T, initial, N):
t=np.linspace(t0, T, N+1)
u=np.zeros(t.shape)
h=(T-t0)/N
u[0]=initial
for n in range (N):
tval = t[n]
uval = u[n]
k1 = odefunc(tval, uval);
k2 = odefunc(tval+h, uval+h*k1)
u[n+1] = uval + 0.5*h*(k1+k2)
return h, t, u
In [7]:
#右辺の関数
def func1(t, y):
return np.cos(2*y)
N=20
t0=0.0
T=1.0
u0=0
#Euler法
h_euler, t_euler, u_euler = euler(func1, t0, T, u0, N)
#Heun法
h_heun, t_heun, u_heun = heun(func1, t0, T, u0, N)
#結果の描画
plt.plot(t_euler, u_euler,'b')
plt.plot(t_heun, u_heun,'r')
plt.xlabel('t')
plt.ylabel('u')
plt.legend(['Euler','Heun'])
plt.grid('on')
plt.show()
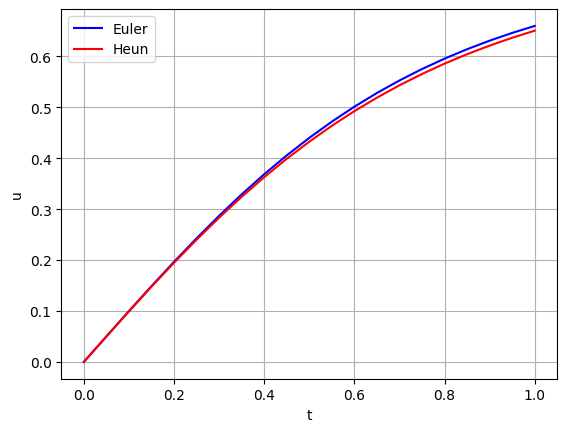
In [8]:
#右辺の関数
def func1(t, y):
return np.cos(2*y)
#厳密解
def exact1(t):
return 0.5*np.arcsin( (np.exp(4*t)-1) / (np.exp(4*t)+1) )
t0=0.0
T=1.0
u0=0
hv_euler, ev_euler, rate_euler= OderError(euler, func1, exact1, t0, T, u0)
hv_heun, ev_heun, rate_heun= OderError(heun, func1, exact1, t0, T, u0)
for i in range(rate_euler.shape[0]-1):
print(f'{hv_euler[i+1]:.3f}, {rate_euler[i]:.3f}, {rate_heun[i]:.3f}')
#結果の描画(両対数目盛)
plt.plot(hv_euler, ev_euler, 'bo-')
plt.plot(hv_heun, ev_heun, 'ro-')
plt.xscale('log')
plt.yscale('log')
plt.legend(['Euler','Heun'])
plt.xlabel('h')
plt.ylabel('error')
plt.grid('on')
plt.gca().set_aspect('equal', adjustable='box')
plt.show()
Out [8]:
0.125, 1.084, 2.212
0.062, 1.035, 2.109
0.031, 1.019, 2.055
0.016, 1.009, 2.027
0.008, 1.005, 2.014
0.004, 1.002, 2.007
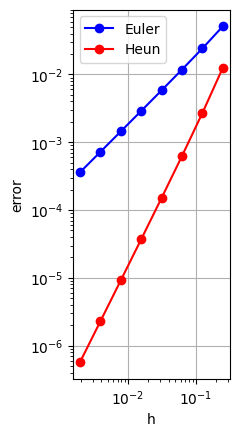
これで,Heun法の誤差が,$\mathcal{E}_h\approx Ch^2$ であることが実験的に確かめられた.
この考え方を一般化して, \begin{align*} \tag{6.8a} {U}_{n+1}&={U}_n+\displaystyle{h\sum_{i=1}^s c_i{k}_i},\\ \tag{6.8b} {k}_i&=\displaystyle{{f}\Big(t_n+\alpha_i h,{U}_n+h\sum_{j=1}^{i-1}\beta_{ij}{k}_j\Big)}\quad (i=1,\ldots,s) \end{align*} という近似解法を考えることができる. ただし,$\sum^{0}_{j=1}$ が出てきた場合にはこの項は考慮しな いことにする.また,$s\ge 1$ は整数であり. $s+s+\frac{s(s+1)}{2}$ 個の係数 $\{c_i\}$,$\{\alpha_i\}$, $\{\beta_{ij}\}$ は,解法が $p\ge 1$ に対して $p$ 次精度となるように定める. 近似解法(6.8a,b)を $s$ 段数 $p$ 次精度のRunge--Kutta法と呼ぶ. もう少し正確には, 陽的なRunge--Kutta法と呼ばれる.したがって,陰的な Runge--Kutta法も存在するが,この講義では扱わない.
例6.3 (3次精度のRunge--Kutta法の例)
次は,Kutta法と呼ばれる: \begin{align*} U_{n+1}&=U_n+\frac{h}{6}(k_1+4k_2+k_3),\\ k_1&=f(t_n,U_n),\\ k_2&=f\left(t_n+\mbox{$\frac12$}h, U_n+\mbox{$\frac12$}hk_1\right),\\ k_3&=f\left(t_n+ h, U_n+h(-k_1+2k_2)\right).\\ \end{align*}
次は,SSPRK3(strong stability preserving Runge--Kutta medhod of the 3rd order)と呼ばれる: \begin{align*} U_{n+1}&=U_n+\frac{h}{6}(k_1+k_2+4k_3),\\ k_1&=f(t_n,U_n),\\ k_2&=f\left(t_n+h, U_n+hk_1\right),\\ k_3&=f\left(t_n+\mbox{$\frac12$} h, U_n+\mbox{$\frac14$} h(k_1+k_2)\right).\\ \end{align*} これらは,3段数3次精度の公式である.もちろん,それを確かめるのためには,相当な計算をする必要がある.$\blacksquare$
例6.4 (4次精度のRunge--Kutta法の例)
Runge--Kutta法の中で,最も有名なのは,次の公式である. これを,本講義では,古典的Runge--Kutta法と呼ぶ. \begin{align*} U_{n+1}&=U_n+\frac{h}{6}(k_1+2k_2+2k_3+k_4),\\ k_1&=f(t_n,U_n),\\ k_2&=f\left(t_n+\mbox{$\frac12$} h, U_n+\mbox{$\frac12$} hk_1\right),\\ k_3&=f\left(t_n+\mbox{$\frac12$} h, U_n+\mbox{$\frac12$} hk_2\right),\\ k_4&=f\left(t_n+ h, U_n+hk_3\right) . \end{align*} これは4段数4次精度である.$\blacksquare$
例6.5(Fehlberg法)
6段数5次のRunge-Kutta法,あるいは,5次のFehlberg法とは,次のもの: \begin{align*} U_{n+1}&=U_n+h\left(\mbox{$\frac{16}{135}$}k_1+\mbox{$\frac{6656}{12825}$}k_3+\mbox{$\frac{28561}{56430}$}k_4 -\mbox{$\frac{9}{50}$}k_5+\mbox{$\frac{2}{55}$}k_6\right)\equiv \Phi_5(h,U_n)\\ k_1&=f(t_n,U_n)\\ k_2&=f\left(t_n+\mbox{$\frac{1}{4}$}h, U_n+h\cdot \mbox{$\frac{1}{4}$} k_1\right)\\ k_3&=f\left(t_n+\mbox{$\frac{3}{8}$}h, U_n+h\left(\mbox{$\frac{3}{32}$}k_1+\mbox{$\frac{9}{32}$}k_2\right)\right)\\ k_4&=f\left(t_n+\mbox{$\frac{12}{13}$}h, U_n+h\left( \mbox{$\frac{1932}{2197}$}k_1-\mbox{$\frac{7200}{2197}$}k_2+\mbox{$\frac{7296}{2197}$}k_3\right)\right)\\ k_5&=f\left(t_n+h, U_n+h\left( \mbox{$\frac{439}{216}$}k_1-8k_2+\mbox{$\frac{3680}{513}$}k_3-\mbox{$\frac{845}{4104}$}k_4\right)\right)\\ k_6&=f\left(t_n+\mbox{$\frac{1}{2}$}h, U_n+h\left( -\mbox{$\frac{8}{27}$}k_1+2k_2-\mbox{$\frac{3544}{2565}$}k_3+\mbox{$\frac{1859}{4104}$}k_4-\mbox{$\frac{11}{40}$}k_5\right)\right). \end{align*} 実は,5次のFehlberg法と同じ $k_1,\ldots,k_5$ を用いて,5段数4次のRunge--Kutta法(4次のFehlberg法)を構成できる: \begin{equation*} U_{n+1}=U_n+h\left(\mbox{$\frac{25}{216}$}k_1+\mbox{$\frac{1408}{2565}$}k_3+\mbox{$\frac{2197}{4104}$}k_4 -\mbox{$\frac{1}{5}$}k_5\right)\equiv \Phi_4(h,U_n). \end{equation*} $U_n$ が与えられたとする.そして, $k_1,\ldots,k_5$ を計算して,4次と5次のFehlberg法を考えると, \begin{gather*} \Phi_5(h,U_n)-\Phi_4(h,U_n)=\sum_{i=1}^6d_ik_i,\qquad d_i=\frac{\overline{d}_i}{752400},\\ \overline{d}_1=2090,\ \overline{d}_2=0,\ \overline{d}_3=-22528,\ \overline{d}_4=-21970,\ \overline{d}_5=15048,\ \overline{d}_6=27360 \end{gather*} となる.この関係は,後で役に立つ.$\blacksquare$
注意.係数をうまく選べば,いくらでも良い解法が作れそうな気がするが,そううまくはいかない.実際,$p$ 次精度のRunge--Kutta法を構成するには,少なくとも $p$ 段数が必要である.すなわち,$s$ 段数のRunge--Kutta法は,$s+1$ 次以上の精度にはなり得ない. さらに,$s\ge 5$ のとき,$s$ 段数 $s$ 次精度のRuneg--Kutta法は存在しない.$\blacksquare$
注意. Euler法の解析と同様に考えると,$t_{n-1}$まで誤差が混入してない,すなわち, $u(t_k)=U_{k}$ $(k=1,\ldots,n-1)$ を仮定すると,$p$ 次精度の公式は, $h$ が十分小さければ,適当な定数 $c$ が存在して,$u(t_n)-U_n=ch^{p+1}+O(h^{p+2})$ という関係があると考えられる.すなわち,$p$ 次精度の公式は,局所的には $p+1$ 次精度である.$\blacksquare$.
刻み幅の自動調節,あるいは,RKF45公式
刻み幅 $h$ を可変 \begin{equation*} t_{n+1}=t_n+h_{n},\quad h_{n}>0\qquad (n\ge 0) \end{equation*} として,指定された許容誤差限界 $\varepsilon > 0$ に対して, \begin{equation} \tag{6.9} \max_{0\le t_n\le T}|u(t_n)-U_n|\le \varepsilon \end{equation} となるように,$h_n$ を自動調節する方法を考えよう.これを,刻み幅の自動調整という.
以下で説明するのは,RKF45公式と呼ばれる刻み幅の自動調整法である.4次と5次のFehlberg法 \[ U_{n+1}\stackrel{\textrm{def.}}{=} \Phi_5(h_n,U_n)=U_n+h_n(\cdots\mbox{略}\cdots),\qquad U_{n+1}^*\stackrel{\textrm{def.}}{=} \Phi_4(h_n,U_n)=U_n+h_n(\cdots\mbox{略}\cdots) \] を組み合わせる.ただし,$U_{n+1}^*$ は誤差の推定にのみ利用し, 近似値としては $U_{n+1}$ を採用する.ここで,同一の $U_n$ を使って,値を更新していることに注意せよ.
- (6.9)を実現するために, \begin{equation} \tag{6.10} |U_n\to U_{n+1}\mbox{の計算で混入する誤差}| \le \varepsilon \frac{h_{n}}{T} \end{equation} を要請する. そのために,$t_{n-1}$ までは,(6.10)が実現されていると仮定する. ただし,左辺は計算できない量なので,なんらかの代用品を考えなければならない.
- とりあえず, $h_{n}= h_{n-1}$ (前刻み幅),または,$h_n=h_{-1}$ (初期設定値)とする.
- [$*$] $U_{n+1}=\Phi_5(h_{n},U_n)$, $U_{n+1}^*=\Phi_4(h_{n},U_n)$, $U_{n+1}-U_{n+1}^*=\sum_{i=1}^6d_ik_i$ を計算する.$U_{n}^*=U_n$ としてることに注意せよ.
- $U_{n+1}$ は5次精度,$U_{n+1}^*$ は4次精度の公式による近似解なので, \begin{align*} U_{n+1}-U_{n+1}^* &=\underbrace{(U_{n+1}-u(t_{n+1}))}_{\approx 0}+(u(t_{n+1})-U^*_{n+1})\\ &\approx u(t_{n+1})-U^*_{n+1} \end{align*} と考えることにしよう.すなわち,計算可能な, $e_{n}\stackrel{\textrm{def.}}{=} |U_{n+1}-U_{n+1}^*|$ を,計算不可能な $|u(t_{n+1})-U^*_{n+1}|$ の推定値として採用するのである. そして,(6.10)の代わりに, \begin{equation} \tag{6.11} e_{n}\le \varepsilon\frac{h_{n}}{T} \end{equation} を要請することにする. 実際,$|u(t_{n+1})-U(t_{n+1})|$ は $e_{n+1}$ よりも小さいはずなので,こうしておけば十分であろう.
- さて,はじめから,(6.11)が成立していれば, $h_{n},U_{n+1}$ は確定する.
- (6.11)が成立していないとき, $0 < \overline{h} < h_{n}$ をうまく選んで,対応する $\overline{U}_{n+1}=\Phi_5(\overline{h},U_n)$, $\overline{U}^*_{n+1}=\Phi_4(\overline{h},U_n)$, $\overline{e}_{n}=|\overline{U}_{n+1}-\overline{U}^*_{n+1}|$ が,$\displaystyle{\overline{e}_{n}\le\varepsilon\frac{\overline{h}}{T}}$ となるようにしたい.
- 次のように考える.まず,Euler法と Runge--Kutta法の項の最後の注意を思い出す.すると, $U_{n+1}$ は5次精度の公式, $U_{n+1}^*$ は4次精度の公式なので,適当な$c_1,c_2$ が存在して, \[ u(t_{n+1})-U_{n+1}=c_1h_{n}^6+O(h_{n}^7),\qquad u(t_{n+1})-U_{n+1}^*=c_2h_{n}^5+O(h_{n}^6) \] と考えられる.ゆえに, $U_{n+1}-U_{n+1}^*=-c_2h^5_{n}+O(h_{n}^6)$である. したがって,$e_{n}\approx |c_2|h_{n}^5$, $\overline{e}_{n}\approx |c_2|\overline{h}^5$ がわかる. ゆえに, \begin{equation*} \overline{e}_{n}\approx \left(\frac{\overline{h}}{h_{n}}\right)^5e_{n} \le \varepsilon\frac{\overline{h}}{T}. \end{equation*} したがって,$\overline{h}$ を, \begin{equation} \tag{6.12} \overline{h}=\gamma\cdot h_{n}\left(\frac{\varepsilon h_{n}}{Te_{n}}\right)^\frac14 \end{equation} と選べばよい.ただし,$0<\gamma<1$は適当に選ぶ(例えば,$\gamma=0.9$など).
- あらためて,$h_{n}=\overline{h}$ とおいて,[$*$]に戻る.
以上は,推定値等に基づいた議論なので, (6.12)のように選んでも,確実に $\displaystyle{\overline{e}_{n}\le\varepsilon \overline{h}/T}$ となる保証 はない.実際にはこの条件が成立するまで,この制御を繰 り返すことになる.詳しくは,[森]を参照せよ.
連立微分方程式
$m$ 成分の連立微分方程式を考える: \begin{equation} \tag{6.13} \frac{d\boldsymbol{u}(t)}{dt}=\boldsymbol{f}(t,\boldsymbol{u}(t)),\qquad \boldsymbol{u}(t_0)=\boldsymbol{a}. \end{equation} ただし, \begin{equation*} \boldsymbol{u}(t)=\left(\begin{array}{c} u_1(t)\\ \vdots\\ u_m(t) \end{array}\right), \quad \boldsymbol{f}(t,\boldsymbol{u})=\left(\begin{array}{c} f_1(t,\boldsymbol{u})\\ \vdots\\ f_m(t,\boldsymbol{u}) \end{array}\right),\quad \boldsymbol{a} =\left(\begin{array}{c} a_1\\ \vdots\\ a_m \end{array}\right) . \end{equation*} 引き続き,$h=(T-t_0)/N$ とおいて,一様刻み幅 $t_n=t_0+nh$ $(n=0,1,\ldots,N)$ を考え, $\boldsymbol{U}_n=(U_{n,1},\ldots,U_{n,m}) \approx \boldsymbol{u}(t_n)$ を求めることを考える.以下,特に断らなくても,$\boldsymbol{U}_0=\boldsymbol{a}$ とする.
このようにベクトル値の初期値問題に対しても,上記の解析は,絶対値をしかるべく$\mathbb{R}^m$ のノルムに変更すれば,ほぼ同様に遂行できる.結果として,次の公式を得る.
Euler法(前進Euler法) \begin{equation*} \boldsymbol{U}_{n+1}=\boldsymbol{U}_n+h\boldsymbol{f}(t_n,\boldsymbol{U}_n). \end{equation*}
Heun 法 \begin{eqnarray*} \boldsymbol{U}_{n+1}&=&\boldsymbol{U}_n+\frac{h}{2}\left(\boldsymbol{k}_1+\boldsymbol{k}_2\right),\\ \boldsymbol{k}_1 &=& \boldsymbol{f}(t_n,\boldsymbol{U}_n),\\ \boldsymbol{k}_2 &=& \boldsymbol{f}(t_n+h,\boldsymbol{U}_n+h\boldsymbol{k}_1). \end{eqnarray*}
SSPRK3法 \begin{eqnarray*} \boldsymbol{U}_{n+1}&=&\boldsymbol{U}_n+\frac{h}{6} \left(\boldsymbol{k}_1+\boldsymbol{k}_2+4\boldsymbol{k}_3\right),\\ \boldsymbol{k}_1 &=& \boldsymbol{f}(t_n,\boldsymbol{U}_n), \\ \boldsymbol{k}_2 &=& \boldsymbol{f}\left(t_n+h,\boldsymbol{U}_n+h\boldsymbol{k}_1\right),\\ \boldsymbol{k}_3 &=& \boldsymbol{f}\left(t_n+\frac{1}{2}h,\boldsymbol{U}_n+\frac{1}{4}h(\boldsymbol{k}_1+\boldsymbol{k}_2)\right). \end{eqnarray*}
古典的Runge--Kutta 法 \begin{eqnarray*} \boldsymbol{U}_{n+1}&=&\boldsymbol{U}_n+\frac{h}{6} \left(\boldsymbol{k}_1+2\boldsymbol{k}_2+2\boldsymbol{k}_3+\boldsymbol{k}_4\right),\\ \boldsymbol{k}_1 &=& \boldsymbol{f}(t_n,\boldsymbol{U}_n), \\ \boldsymbol{k}_2 &=& \boldsymbol{f}\left(t_n+\frac{1}{2}h,\boldsymbol{U}_n+\frac{1}{2}h\boldsymbol{k}_1\right),\\ \boldsymbol{k}_3 &=& \boldsymbol{f}\left(t_n+\frac{1}{2}h,\boldsymbol{U}_n+\frac{1}{2}h\boldsymbol{k}_2\right), \\ \boldsymbol{k}_4 &=& \boldsymbol{f}\left(t_n+h,\boldsymbol{U}_n+{h}\boldsymbol{k}_3\right). \end{eqnarray*}
Fehlberg法 省略.
$s$ 段数 $p$ 次精度という用語は,ベクトル値の場合でも同じである(ただし,絶対値をしかるべく$\mathbb{R}^m$ のノルムに変更する).実際, Euler法は1段数1次精度の, Heun法は2段数2次精度の, SSPRK3法は3段数3次精度の, 古典的Runge--Kutta法は4段数4次精度の公式である.
例6.6
$x$ 軸上におかれた質量 $1$ の質点の運動を考える.時刻 $t$ における質点の位置 を $x(t)$ で表す.$\omega$ を正定数として,質点に $-\omega^2x(t)$ の外力が働 く場合を考えると,ニュートンの運動の法則により, $d^2x(t)/dt^2=-\omega^2x(t)$ を得る.これは単振動の微分方程式と呼ばれる.さらに,速度に比例する抵抗 $\gamma dx(t)/dt$ ($\gamma$ は正定数)が働く場合には,方程式は, \begin{equation*} \frac{d^2}{dt^2}x(t)=-\omega^2x(t)-\gamma \frac{d}{dt}x(t) \end{equation*} となる.この方程式は,$u_1(t)=x(t)$,$u_2(t)=dx(t)/dt$ とおくことで, \begin{align*} \frac{d}{dt}u_1(t)&=\frac{d}{dt}x(t)=u_2(t),\\ \frac{d}{dt}u_2(t)&=\frac{d^2}{dt^2}x(t)=-\omega^2x(t)-\gamma \frac{d}{dt}x(t)=-\omega^2u_1(t)-\gamma u_2(t), \end{align*} すなわち, \[ \frac{d}{dt} \begin{pmatrix} u_1(t)\\ u_2(t) \end{pmatrix} = \begin{pmatrix} u_2(t)\\ -\omega^2 u_1(t)-\gamma u_2(t) \end{pmatrix} = \begin{pmatrix} 0 & 1\\ -\omega^2 &-\gamma \end{pmatrix} \begin{pmatrix} u_1(t)\\ u_2(t) \end{pmatrix} \] となる.
$\omega=2$, $\gamma=0.5$, $t_0=0$, $T=5$ に対して,Heun法を試してみよう.初期値の次元($\boldsymbol{a}\in\mathbb{R}^m$ であるときの $m$ のこと)に合わせて,ベクトル値で計算を行うように,In [9] で定めたheunを次のように修正する.
In [9]:
def heunvec(odefunc, t0, T, initial, N):
t=np.linspace(t0, T, N+1)
u=np.zeros((t.shape[0],initial.shape[0]))
h=(T-t0)/N
u[0,:]=initial
for n in range(N):
tval=t[n]
uval=u[n,:]
k1 = odefunc(tval, uval)
k2 = odefunc(tval+h, uval+h*k1)
u[n+1,:] = uval + (h/2)*(k1 + k2)
return h, t, u
In [10]:
def harmonic(t, u):
omega=2
gamma=0.5
return np.array([u[1],-omega**2*u[0]-gamma*u[1]])
N=100
t0=0.0
T=6.0
u0=np.array([1,0.0])
h, t, u = heunvec(harmonic, t0, T, u0, N)
plt.plot(t,u[:,0],'b')
plt.plot(t,u[:,1],'r')
plt.xlabel('t')
plt.legend(['x','dx/dt'])
plt.grid('on')
plt.gca().set_aspect('equal', adjustable='box')
plt.show()
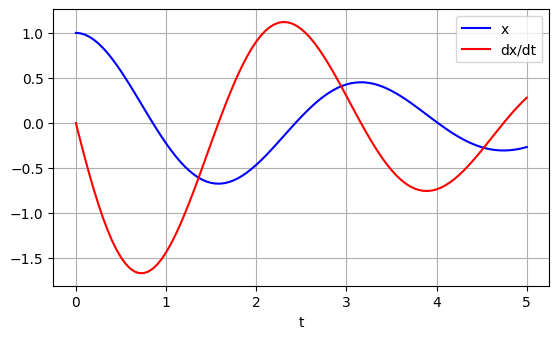
注意.上では,「ベクトル値の初期値問題に対しても,上記の解析は,ほぼ同様に遂行できる」と書いたが,本当のことを言えば,これは言い過ぎである.実際, 2段数2次精度の公式の導出において,スカラー値の場合([齊藤2017]の4.2節)とベクトル値の場合([齊藤2012]の8.4節)では,微妙に途中の計算が異なる(スカラー値では現れない項が,ベクトル値では現れることがある).しかし結果として,Heun法は同一の形をしている.また,名前のついている公式は,総じて,スカラー値でもベクトル値でも同じであると思って良い. $\blacksquare$
付録:課題1.1に対するコメント
レポート問題として課題1.1を選んだ人が多かった.課題は,階段関数 \begin{equation*} f(x)= \begin{cases} 1 & (0 < x < \pi)\\ 0 & (x=-\pi,0)\\ -1 & (-\pi < x <0) \end{cases} \end{equation*} のFourier級数展開 \begin{equation*} f(x)=\frac{4}{\pi} \sum_{k=1}^\infty \frac{\sin (2k-1)x}{2k-1} \label{eq:6.20} \end{equation*} の部分和 \begin{equation*} S_n(x)=\frac{4}{\pi} \sum_{k=1}^n \frac{\sin (2k-1)x}{2k-1} \end{equation*} について,例えば,$n=1,10,20,50$などのときのグラフを描画せよ,というものであった.
さて,多くの人のレポートでは図6.01のようなグラフが描画されていた. 一方で,図6.02のようなグラフを描画している人も少なからず居た. この8つの図を良く見比べて欲しい.実は,図6.01は不正確である.
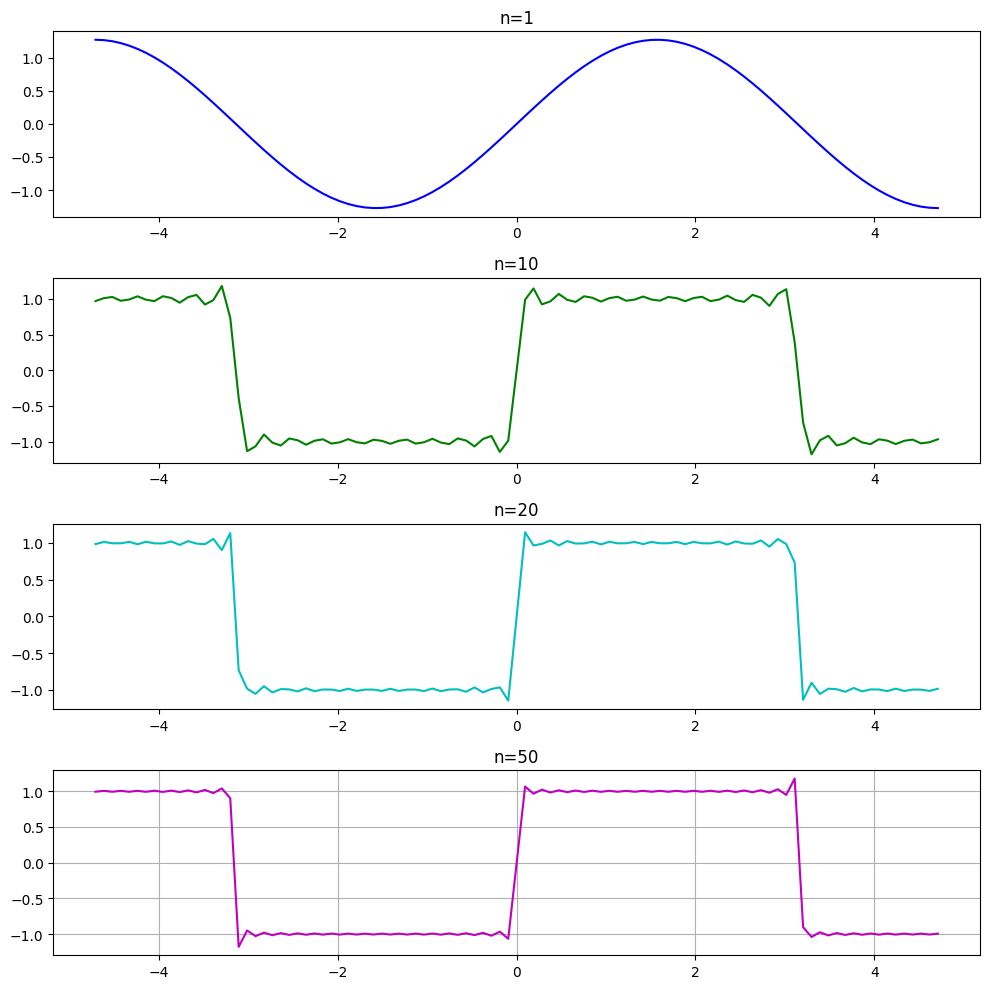
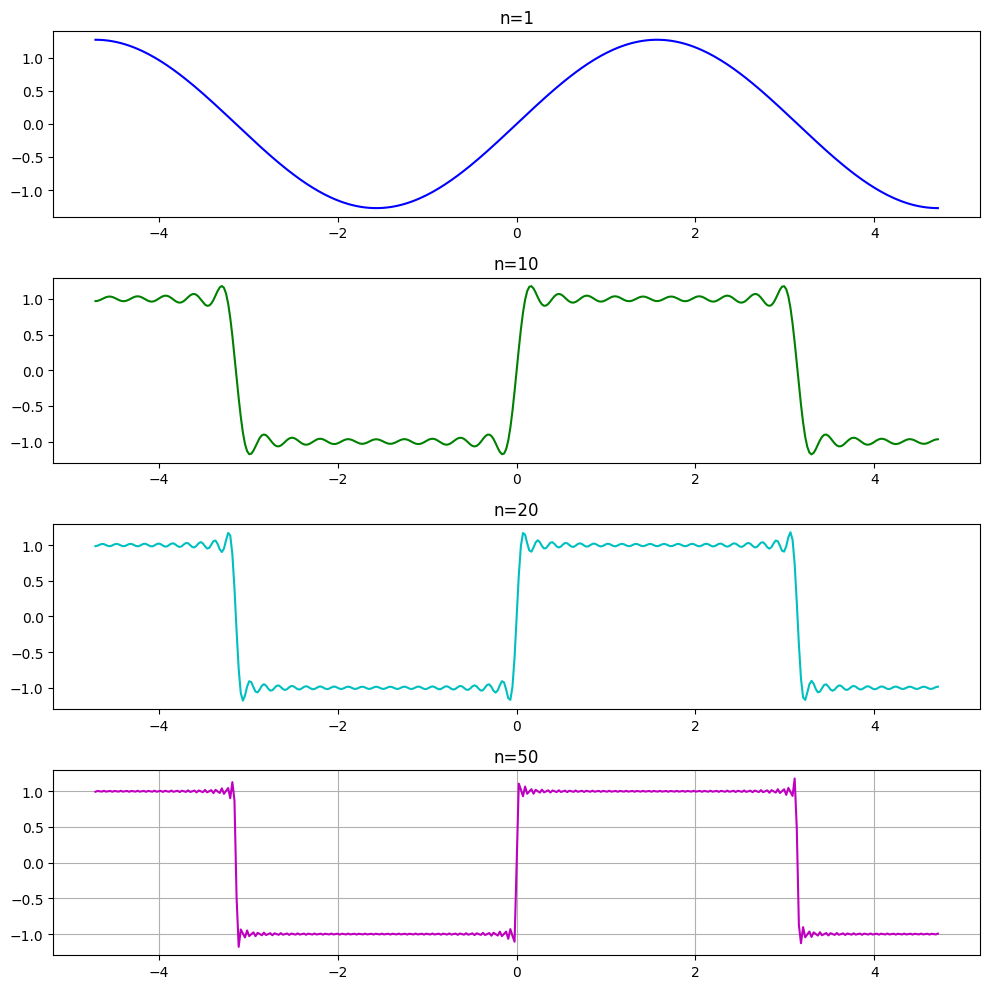
Fourier級数の一般論により,$-\pi\le x\le \pi$ を固定すると, \begin{equation*} S_n(x)\to \frac{f(x-0)+f(x+0)}{2}\qquad (n\to\infty) \end{equation*} となる.$x$ が連続点ならば,$S_n(x)\to f(x)$ となるが, 不連続点の場合には,その近傍で振動を生ずる.これをGibbsの現象と言うのであった. もし,$f$ が滑らかな周期関数であれば,$S_n$ は $f$ に一様収束するが,いまは,$f$ は不連続なので,この定理は使えない.
このことを心にとどめた上で,再度,図6.01と図6.02を比較してみる.この2つの違いは明確である.すなわち,図6.02で確認される不連続点のまわりでの振動現象(Gibbsの現象)が,図6.01では観察できない.Gibbsの現象は,元の関数の不連続性が原因であって,$n$ を大きくしたからといって,解消されるわけではない.すなわち,図6.01は不正確である.
この原因は,描画の際に設定したパラメータの不備にある. 図6.01は,以下のIn [03]で描画した.すなわち,第1回の例題と同じく,$m=100$ としている.一方で, 図6.02は,In [03]で,$m=400$ として描画した. すなわち,$m=100$ では,分割の大きさが適切でなく,あたかも,振動がおとなしいようなグラフを描画してしまうのである.
このような場合には,分割数を適切にとらなければならないことが分かったが,どれくらいが適切なのかは,(いつも)事前にわかる訳ではない.とはいえ,今の場合は,$m$ は描画のためのパラメータであるから,適当に大きくとるのが良いであろう.すなわち,$m$ を順に大きくして,複数の図を 描き,結果に違いがでないのを確認するのが良い).以上のまとめとして,得られる教訓は次のようなものである.
教訓. 元の問題には現れない,計算のために導入したパラメータは,一見,計算がうまく行っているように見えても,複数の組み合わせで試して,結果に違いが出ないかを確認するべきである.
In [01]: import numpy as np import matplotlib.pyplot as plt
In [02]:
def stepfunc(x,n):
val = 0.0;
for i in range(n):
theta=(2*i+1)*x
val += np.sin(theta)/(2*i+1)
return (4.0/np.pi)*val
In [03]:
m=100
x = np.linspace(-1.5*np.pi, 1.5*np.pi, m+1)
plt.figure(figsize=(10, 10))
plt.subplot(4, 1, 1)
y1 = stepfunc(x,1)
plt.plot(x, y1,'b')
plt.title('n=1')
plt.subplot(4, 1, 2)
y2 = stepfunc(x,10)
plt.plot(x, y2,'g')
plt.title('n=10')
plt.subplot(4, 1, 3)
y3 = stepfunc(x,20)
plt.plot(x, y3,'c')
plt.title('n=20')
plt.subplot(4, 1, 4)
y4 = stepfunc(x,50)
plt.plot(x, y4,'m')
plt.title('n=50')
plt.tight_layout()
plt.grid('on')
plt.show()
問題
- 上記の入力と出力をすべて確かめよ.
- パラメータ値を変えて,計算を再試行せよ.
- 例題を自分で設定して,上記の方法を試せ.
課題
課題6.1
自分で常微分方程式の初期値問題(6.1)の例題を作り,Heun法, SPPRK3法,古典的Runge--Kutta法の精度($\mathcal{E}_h\approx Ch^p$ の形の収束性)を比較せよ.例題の作り方は,講義でヒントを言う. ($du/dt=\mbox{定数}$などの,あまり にも明らかなものは避けること).
課題6.2
自分で連立常微分方程式の初期値問題(6.13)の例題を作り,Heun法, SPPRK3法,古典的Runge--Kutta法の精度($\mathcal{E}_h\approx Ch^p$ の形の収束性)を比較せよ.(次回,「6. 常微分方程式の初期値問題(応用編)」の最後の「補足(ベクトル値の場合の誤差の観察方法)」でヒントを述べる.)
課題6.3
次の公式をLambertの方法と言う: \begin{align*} U_{n+1}&=U_n+\frac{h}{6}(k_1+4k_2+k_4),\\ k_1&=f(t_n,U_n),\\ k_2&=f\left(t_n+\mbox{$\frac12$} h, U_n+\mbox{$\frac12$} hk_1\right),\\ k_3&=f\left(t_n- h, U_n+\mbox{$\frac12$} h(k_1-3k_2)\right),\\ k_4&=f\left(t_n+ h, U_n+\mbox{$\frac13$}h(4k_2-k_3)\right). \end{align*} 次の2つの初期値問題に対して,Lambertの方法を適用し,その精度を比較せよ.その結果から,何が予想されるかを考察せよ.また,その予想を,別の例を用いて検証せよ. \begin{gather} \frac{du(t)}{dt}=-\frac{1}{2e^t-1}u(t)\quad (0 < t <1),\qquad u(0)=2,\\ \frac{du(t)}{dt}=u(t)[1-u(t)]\quad (0 < t <1),\qquad u(0)=2. \end{gather}
参考文献
- [齊藤2012] 齊藤宣一,数値解析入門,東京大学出版会,2012年
- [齊藤2017] 齊藤宣一,数値解析(共立講座数学探求),共立出版,2017年
- [森] 森正武,FORTRAN77数値計算プログラミング,岩波書店,1987年.