2024-3S 計算数理演習（東京大学理学部・教養学部） [齊藤宣一] [top] [0] [1] [2] [3] [4] [5] [6] [7] [8] [UTOL]

3. 非線形方程式の反復解法

Newton法

滑らかな関数 $f:I\subset \mathbb{R}\to\mathbb{R}$ に対して，方程式 $f(x)=0$ の解 $a\in I$ を計算することを考える． Newton法では，反復列 $x_1,x_2,\ldots$ を， \begin{equation} \tag{N} x_{k+1}=x_k-\frac{f(x_k)}{f'(x_k)}\qquad (k\ge 0) \end{equation} で生成する．ただし，$x_0$ は初期値として与える．

例題として， \begin{equation} \tag{3.1} f(x)=e^x-2x^2=0 \end{equation} を考えよう．図3.1により（あるいは関数の増減を調べることにより）， 方程式 $f(x)=0$ には3つの（実数）解 $a_1 < a_2 < a_3$ が存在することがわかる．さらに， $-0.7 < a_1 < 0.3$，$1.3 < a_2 < 1.7$，$2.5 < a_3 < 3$ がわかる． このことは，初期値を選ぶ際の重要な情報である．

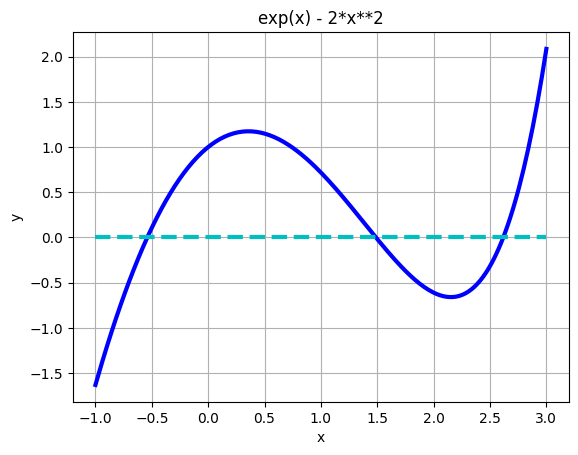
Newton法を実際に実行してみよう．$f(x)$ と $f'(x)$ は具体的な関数形を自分で定義する必要がある．そして，$x_0=-1$ としてみる．

In [1]:  
import numpy as np

def f(x):
  return np.exp(x) - 2.0*x**2.0
def dfdx(x):
  return np.exp(x) - 4.0*x
    
x=-1.0 
eps=1e-12  
while np.abs(f(x)) > eps:
  x = x - f(x)/dfdx(x)
  print(f'{x:.15f}, {f(x):.4e}')

Out [1]: 
-0.626335712601346, -2.5005e-01
-0.544080790288722, -1.1673e-02
-0.539846453645709, -3.0649e-05
-0.539835276980653, -2.1343e-10
-0.539835276902820, 0.0000e+00

この計算では，$|f(x_k)|\le \textrm{eps}=10^{-12}$ を満たす最小の $k$ が見つかった時点で計算を終了し，結果として，$(x_k,f(x_k))$ を表示する．実際，この計算から，$a_1\approx -0.5398352769\cdots$ であることがわかる．

この例では，運良く収束してくれたが，Newton法の反復列がいつも収束するとは限らない． 特に，反復の途中で，$f'(x_k)\approx 0$となってしまう場合には，計算を継続することはできない．これらのことを考慮して，上の In[1]を，少々整理して書き直そう．

まず，モジュールは（各ノートブックに対して）一度インポートしておけば良い．今回使う予定のモジュールを，はじめにまとめて，読み込んでおこう．

In [2]:  
import numpy as np
import sys
import matplotlib.pyplot as plt

次に，Newton法の反復計算を実行する関数を定義する．

In [3]:  
def newton1(f, dfdx, x, eps, maxiter):
  iter = 0
  fval = f(x)
  xvect = np.array([x])
  fvect = np.array([fval])
  while np.abs(fval) > eps and iter < maxiter:
    dfdxval = dfdx(x)
    if abs(dfdxval)<1.0e-15:
      print('derivative is almost zero for x = ', x)
      sys.exit(1)    
    x -= fval/dfdxval
    fval = f(x)
    iter += 1
    xvect=np.append(xvect,x)
    fvect=np.append(fvect,fval)
  return xvect, fvect, iter

そうして，改めて，関数$f(x)$ と $f'(x)$ を定義して，上で定義した関数newton1を用いて計算する．

In [4]:  
def f(x):
  return np.exp(x) - 2.0*x**2.0
def dfdx(x):
  return np.exp(x) - 4.0*x
    
kmax=20  
x=-1.0
eps=1e-12
xvect, fvect, iter= newton1(f, dfdx, x, eps, kmax)
  
print(f'max number of iterations: {kmax:d}')  
for i in range(iter+1):
  print(f'{i:d}, {xvect[i]:.15f}, {fvect[i]:.3e}')

Out [4]: 
max number of iterations: 20
0, -1.000000000000000, -1.632e+00
1, -0.626335712601346, -2.500e-01
2, -0.544080790288722, -1.167e-02
3, -0.539846453645709, -3.065e-05
4, -0.539835276980653, -2.134e-10
5, -0.539835276902820, 0.000e+00

結果は，（同じ計算をしているのだから）同じである．ただし，In[4]では，反復回数 $k$ が $k_{\max}$ に達した時点で，収束しているか否かに関わらず，反復を終了する．また，$|f'(x_k)|<10^{-15}$ となった時点で，derivative is almost zeroというエラーメッセージの出力とともに，計算を途中で強制終了する（そのためにsysモジュールを用いた）．

In[4]では（そして，この講義を通じて），十分小さな $\mathrm{eps}$ に対して　$|f(x_k)|<\mathrm{eps}$ となった際に，反復列が収束し，近似解が求まったと判断している．このとき，最終的な結果だけを見るのではなく，収束の様子を，しっかりと確認するべきである．なお，より妥当な停止基準を考えることもできる．例えば，[齊藤2017]の1.4節，[杉原・室田]の4.1節や[伊理・藤野]の第9章をみよ．ただし，実際の応用上の興味の対象である多変数の場合に，同様の基準を設けることは，今日的にも難しい（と私は思っている）ので，本講義では，詳しくは扱わない．

念の為確認しておくと，np.appendで配列の最後尾に，要素を追加できる．

In [5]:  
import numpy as np
a=np.array([1,2,3,4])
a=np.append(a,-10)
print(a)

Out [5]: 
[  1   2   3   4 -10]

上で「$a_1\approx -0.5398352769\cdots$ であることがわかる」と書いたが，実際には，別の初期値 $x_0$（で $a_1$ に収束するもの）も用いて結果を確かめておくべきである．もちろん，初期値を変えれば得られる解は変わるし，反復列が収束しない場合もあり得る．これについては，ある程度の見積もりを得ることはできる．すなわち，例えば $a_1$ を計算する際には， $a_1$ を含むような閉区間$J$で，$g(x)=x-f(x)/f'(x)$ に対して $|g'(x)|<1$ $(x\in J)$ となるものを探しておいて，$x_0\in J$ とすれば良いのである（例えば，[齊藤2012]の命題4.3.4）．

理論的な内容を復習しておこう（[齊藤2012]の命題4.3.2と定理4.3.12）．

縮小写像の定理 $g:I\subset \mathbb{R}\to\mathbb{R}$ に対して， 次を満たす閉区間 $J\subset I$ と定数 $0<\lambda<1$ の存在を仮定する:

• $x\in J\ \Rightarrow\ g(x)\in J$
• $x,\ x'\in J\ \Rightarrow\ |{g}(x)-{g}(x')|\le \lambda |x-x'|$．

1. $J$ 内に $a=g(a)$ を満たす $a$ が唯一存在する．この $a$ を $g$ の $J$ における不動点と呼ぶ．
2. 初期値を $x_0\in J$ と選ぶ限りにおいて， 反復法 $x_{k+1}={g}(x_{k})$ によって $J$ 内の反復列 $x_1,x_2,\ldots$ が生成され， \begin{equation} \tag{3.2} |x_k-a|\le \frac{1}{1-\lambda}\lambda^k|x_1-x_0|. \end{equation} を満たす．$\blacksquare$

定理（ニュートン法の収束） $f:I\subset \mathbb{R}\to\mathbb{R}$に対して，次を仮定する：

• $f$: $C^2$級，
• 方程式$f(a)=0$には唯一の解$a\in I$が存在，
• $f'(a)\ne 0$．

一般に，$p>1$と $C>0$ に対して， \begin{equation} \tag{3.3} |x_{k+1}-a|\le C|x_{k}-a|^p\quad (k\mbox{ は十分大}) \end{equation} を満たす数列は，$a$ に $p$ 次収束すると言われる． すなわち，Newton法で生成される反復列は，上の定理の仮定が満たされる際には，2次収束することが保証される．（なお，証明を検討すれば，一般には，2次収束よりも速い収束を保証することはできないこともわかる．）一方で，適当な $0 < M < 1$が存在して， \begin{equation} \tag{3.4} |x_{k+1}-a|\le M|x_{k}-a|\qquad (k\mbox{ は十分大}) \end{equation} を満たす数列は，$a$ に線形収束すると言われる．縮小写像の定理において，収束が保証される数列は，必ず線形収束する．実際，(3.2)は，(3.4)の結果として得られる．

なお，実は，$p$ 次収束はもう少し一般的に定義した方が便利であるが，この講義では，上のように定義して話を進める．（興味のある人は，[齊藤2012]の4.3節を見よ．）

収束の速さ

次に収束の速さについて考察する．特に，Newton法で生成した反復列が，2次収束することを，計算で実験的に確かめたい．

そこで，つぎのように考える．数列が(3.3)を等号で満たすと仮定する．すなわち， $e_k=|x_k-a|$ とおいて，$e_{k+1}=Ce_k^p$ を仮定する．このとき， \[ p= \frac{\log (e_{k+1}/e_k)}{\log (e_{k}/e_{k-1})} \] が成り立つ．そこで，改めて，（今，勝手に仮定したことは忘れて） \begin{equation} \tag{3.5} p_k= \frac{\log (e_{k+1}/e_k)}{\log (e_{k}/e_{k-1})} \end{equation} と定義して，この量を観察する．

次のIn[7]では，In[6]で定義した関数newton_rate1を用いて，これを計算している．ただし，newton1で，$\textrm{eps}=10^{-18}$ として，十分良い近似値を求めておき，これを $a$ の代用とする．すなわち，$a=-0.539835276902820$とする．また，収束の様子を，観察するために，わざと，初期値を遠くにとっておく．

In [6]:  
def newton_rate1(xvect, xsol):
  e = np.array([np.abs(x-xsol) for x in xvect])
  q = np.array([np.log(e[k+1]/e[k]) / np.log(e[k]/e[k-1]) for k in range(1,len(e)-1, 1)])
  return q

In [7]:  
def f(x):
  return np.exp(x) - 2.0*x**2.0
def dfdx(x):
  return np.exp(x) - 4.0*x
    
kmax=20  
x=-20.0
eps=1e-6
xvect, fvect, iter = newton1(f, dfdx, x, eps, kmax)

xsol=-0.539835276902820
q = newton_rate1(xvect, xsol)
for i in range(len(q)):
  print(f'{q[i]:.2f}')

Out [7]: 
1.04
1.09
1.20
1.41
1.70
1.93
2.00

これで，実際に，$k$ が大きければ，$p_k\approx 2.0$となることが，実験的に確かめられた．

次に， \begin{equation} \tag{3.6} f(x)=x^3-x^2-8x+12=(x-2)^2(x+3)=0 \end{equation} を考える．特に，$a=2$ をNewton法で求めてみる．このとき， 反復列が線形収束することは保証されているが，$f'(a)=0$ なので，2次収束は保証されない．

In [8]:  
def f(x):
  return x**3.0 - x**2.0 - 8.0*x + 12.0;
def dfdx(x):
  return 3.0*x**2.0 - 2.0*x - 8.0
    
kmax=20  
x=10.0
eps=1e-6
xvect, fvect, iter = newton1(f, dfdx, x, eps, kmax)

print(f'max number of iterations: {kmax:d}')  
for i in range(iter+1):
     print(f'{i:d}, {xvect[i]:.15f}, {fvect[i]:.3e}')

xsol=2.0
q = newton_rate1(xvect, xsol)
print('rate of convergence')  
for i in range(len(q)):
  print(f'{q[i]:.2f}')

Out [8]: 
max number of iterations: 20
0, 10.000000000000000, 8.320e+02
1, 6.941176470588236, 2.427e+02
2, 4.962364092556454, 6.987e+01
3, 3.713499464117166, 1.971e+01
4, 2.953710886752573, 5.415e+00
5, 2.512216421275264, 1.446e+00
6, 2.267479175300947, 3.769e-01
7, 2.137051113824456, 9.649e-02
8, 2.069427618729226, 2.444e-02
9, 2.034949901678587, 6.150e-03
10, 2.017535391897944, 1.543e-03
11, 2.008782989991313, 3.864e-04
12, 2.004395341905103, 9.668e-05
13, 2.002198635632049, 2.418e-05
14, 2.001099559356707, 6.046e-06
15, 2.000549840109907, 1.512e-06
16, 2.000274935168663, 3.780e-07
rate of convergence
1.06
1.07
1.07
1.06
1.05
1.03
1.02
1.01
1.00
1.00
1.00
1.00
1.00
1.00
1.00

このようになり，近似値が求まるが，先の例と比較すると，反復回数が多くなっている． 実際，収束の速さを調べると，線形収束しかしていないことも確かめられた．

簡易Newton法

Newton法では，各反復ににおいて導関数値を計算しなければならないが，これを効率化する趣旨で，簡易（単純化）Newton法を考える： \begin{equation} \tag{sN} x_{k+1}=x_k-\frac{f(x_k)}{f'(x_0)}\qquad (k\ge 0). \end{equation} ただし，$x_0$ は初期値として与える．見ればすぐにわかるであろうが，導関数値を計算するのは，$k=0$ のときのみである．

次のIn[9]のsimple_newton1は，簡易Newton法を実行するプログラムである．

In [9]:  
def simple_newton1(f, df, x, eps, maxiter):
  if np.abs(df)<1.0e-15:
    print('derivative is almost zero for x = ', x)
    sys.exit(1)    
  iter = 0
  fval = f(x)
  xvect = np.array([x])
  fvect = np.array([fval])
  while np.abs(fval) > eps and iter < maxiter:
    x -= fval/df
    fval = f(x)
    iter += 1
    xvect=np.append(xvect,x)
    fvect=np.append(fvect,fval)
  return xvect, fvect, iter

(3.1)を改めて考えよう．In[9]とIn[6]を実行したのちに，次のIn[10]を実行する．初期値は，$x=-2$ とした．

In [10]:  
def f(x):
  return np.exp(x) - 2.0*x**2.0
def dfdx(x):
  return np.exp(x) - 4.0*x
    
kmax=40  
x=-2
eps=1e-6
xvect, fvect, iter = simple_newton1(f, dfdx(x), x, eps, kmax)

print(f'max number of iterations: {kmax:d}')  
for i in range(iter+1):
     print(f'{i:d}, {xvect[i]:.15f}, {fvect[i]:.3e}')
print('rate of convergence')  
xsol=-0.539835276902820
q = newton_rate1(xvect, xsol)
for i in range(len(q)):
  print(f'{q[i]:.2f}')

Out [10]: 
max number of iterations: 40
0, -2.000000000000000, -7.865e+00
1, -1.033270978644354, -1.779e+00
2, -0.814539154760350, -8.841e-01
3, -0.705864505726745, -5.028e-01
4, -0.644059087236628, -3.045e-01
5, -0.606633736099169, -1.908e-01
6, -0.583177300758487, -1.221e-01
7, -0.568172473081945, -7.908e-02
8, -0.558451912224975, -5.164e-02
9, -0.552103919881243, -3.390e-02
10, -0.547936882472305, -2.233e-02
11, -0.545192275249901, -1.474e-02
12, -0.543380557768382, -9.743e-03
13, -0.542182906237678, -6.447e-03
14, -0.541390430891780, -4.269e-03
15, -0.540865725649776, -2.827e-03
16, -0.540518168273713, -1.873e-03
17, -0.540287887472160, -1.241e-03
18, -0.540135282563353, -8.228e-04
19, -0.540034140461397, -5.454e-04
20, -0.539967101023023, -3.615e-04
21, -0.539922663289220, -2.396e-04
22, -0.539893206271344, -1.589e-04
23, -0.539873679258082, -1.053e-04
24, -0.539860734629196, -6.981e-05
25, -0.539852153432545, -4.628e-05
26, -0.539846464784473, -3.068e-05
27, -0.539842693648058, -2.034e-05
28, -0.539840193666989, -1.348e-05
29, -0.539838536363441, -8.938e-06
30, -0.539837437691655, -5.925e-06
31, -0.539836709351485, -3.928e-06
32, -0.539836226514192, -2.604e-06
33, -0.539835906427576, -1.726e-06
34, -0.539835694232972, -1.144e-06
35, -0.539835553563056, -7.587e-07
rate of convergence
0.54
0.86
0.92
0.96
0.97
0.98
0.99
0.99
1.00
1.00
1.00
1.00
1.00
1.00
1.00
1.00
1.00
1.00
1.00
1.00
1.00
1.00
1.00
1.00
1.00
1.00
1.00
1.00
1.00
1.00
1.00
1.00
1.00
1.00

このように近似解を求めることはできるが，収束は速いとは言えない．実際，線形収束しか観察できない．

多変数のNewton法

2変数の連立方程式 \begin{equation} \tag{3.7} f(x,y)=0,\quad g(x,y)=0 \end{equation} の解 $\boldsymbol{a}=\begin{pmatrix}a\\ b\end{pmatrix}$ を求めるために， \begin{equation} \boldsymbol{x}_{k+1}=\boldsymbol{x}_k-[D{\boldsymbol{f}}(\boldsymbol{x}_k)]^{-1}\boldsymbol{f}(\boldsymbol{x}_k) \end{equation} で点列 $\boldsymbol{x}_k$ を生成する方法を2変数のNewton法と言う．ただし， \[ \boldsymbol{x}_k=\begin{pmatrix} x_k \\ y_k \end{pmatrix} ,\quad \boldsymbol{f}(\boldsymbol{x}_k) =\begin{pmatrix} f(\boldsymbol{x}_k) \\ g(\boldsymbol{x}_k) \end{pmatrix} ,\quad D{\boldsymbol{f}}(\boldsymbol{x}_k)=\begin{pmatrix} f_x(x_k,y_k)&f_y(x_k,y_K)\\ g_x(x_k,y_k)&g_y(x_k,y_k) \end{pmatrix} \] としている．$\boldsymbol{w}=D\boldsymbol{f}(\boldsymbol{x}_k)^{-1}\boldsymbol{f}(\boldsymbol{x}_k)$ の部分の計算は， 逆行列 $D\boldsymbol{f}(\boldsymbol{x}_k)^{-1}$ を具体的に構成し $\boldsymbol{f}(\boldsymbol{x}_k)$ との積を計算するのではなく， 連立一次方程式 \[ [D\boldsymbol{f}(\boldsymbol{x}_k)]\boldsymbol{w}=\boldsymbol{f}(\boldsymbol{x}_k) \] を解いて，$\boldsymbol{w}$ を求めれば良い．

In[11]がこの計算をするプログラムである．

In [11]:  
def newton_mult(f, dfdx, x, eps, maxiter):
  iter = 0
  fval = f(x)
  xvect = np.copy(x)
  fvect = np.copy(fval)
  magnitude = np.linalg.norm(fval, ord=np.inf)
  while magnitude > eps and iter < maxiter:
    dfdxval = dfdx(x)
    if np.abs(np.linalg.det(dfdxval)) < 1.0e-15:
      print('Jacobi matrix is almost singular for x = ', x)
      sys.exit(1)  
    w = np.linalg.solve(dfdxval, fval)
    x -= w
    fval = f(x)
    magnitude = np.linalg.norm(fval, ord=np.inf)
    iter += 1
    xvect=np.vstack((xvect,x))
    fvect=np.vstack((fvect,fval))
  return xvect, fvect, iter

np.vstackは，2次元配列の最後の行に新しい行を追加する．

In [12]:  
A=np.random.rand(3, 4)
print(A)
b=np.array([1,2,3,4])
print(b)
A=np.vstack((A,b))
print(A)

Out [12]: 
[[0.72637584 0.5530919  0.40491219 0.51060388]
 [0.99858932 0.74616897 0.26365743 0.9435761 ]
 [0.51918227 0.90723667 0.53324383 0.4641757 ]]
[1 2 3 4]
[[0.72637584 0.5530919  0.40491219 0.51060388]
 [0.99858932 0.74616897 0.26365743 0.9435761 ]
 [0.51918227 0.90723667 0.53324383 0.4641757 ]
 [1.         2.         3.         4.        ]]

次のIn[13]で記述される関数newton_drawは，In[11]の結果の可視化用に用意しておく．詳しい説明は後回しにして，先に実行する．

In [13]: 
def newton_draw(xvect):
  yvect = xvect[1:,:] - xvect[:-1,:]
  plt.quiver(xvect[:-1,0], xvect[:-1,1], yvect[:,0], yvect[:,1], angles='xy', scale_units='xy', scale=1,color='b')
  plt.plot(xvect[:,0], xvect[:,1],'co',ms=5)
  plt.grid('on')
  plt.gca().set_aspect('equal', adjustable='box')
  plt.show()
  return 0

例題として，連立方程式 \[ f(x,y)=x^2+y^2-1=0,\quad g(x,y)=\sin\left(\frac{\pi x}{2}\right)+y^3=0 \] を考えよう．図3.2に示した概形から， 方程式は$x<0$，$x>0$の範囲にそれぞれ一つずつ解を持つ．

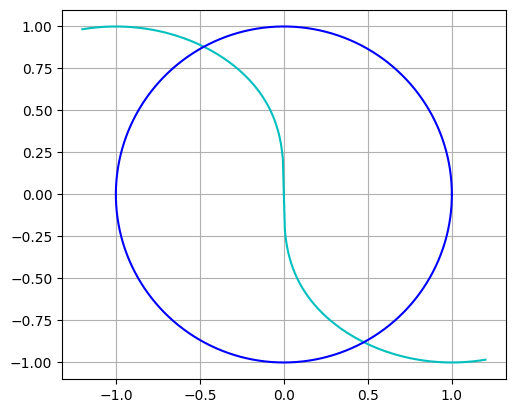
In[11]とIn[13]を実行した上で，次のIn[14]を実行する．初期値は，$\boldsymbol{x}_0=(-1,3)$ としよう．

In [14]:  
def f(x):
  return np.array([x[0]**2.0 + x[1]**2.0 - 1.0, np.sin(np.pi*x[0]/2.0)+x[1]**3.0])

def dfdx(x):
  return np.array([[2.0*x[0], 2.0*x[1]],
             [np.pi/2.0*np.cos(np.pi*x[0]/2.0),3.0*x[1]**2.0]])
    
kmax=20  
x=np.array([-1.0,3.0])
#x=np.array([5.0,-2.0])
eps=1e-12
xvect, fvect, iter= newton_mult(f, dfdx, x, eps, kmax)
  
print(f'max number of iterations: {kmax:d}')  
print('iteration',iter)  
print(xvect)

newton_draw(xvect)

Out [14]: 
max number of iterations: 20
iteration 8
[[-1.          3.        ]
 [ 0.61111111  2.03703704]
 [ 0.08429884  1.33035008]
 [-0.68263798  1.08694277]
 [-0.46438854  0.92618523]
 [-0.47493292  0.88123247]
 [-0.47609424  0.87939695]
 [-0.47609582  0.87939341]
 [-0.47609582  0.87939341]]

これにより， $\boldsymbol{x}_k=\begin{pmatrix} -0.47609582\\ 0.87939341 \end{pmatrix} $ が近似解として採用できることがわかる（これは左上の解である）．

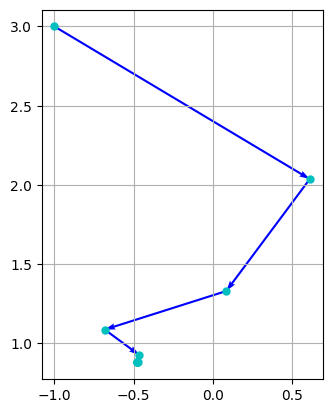
あたらめて，関数newton_drawを説明する．使えれば良い，という立場の人は，（この段階では）読まなくても良い．

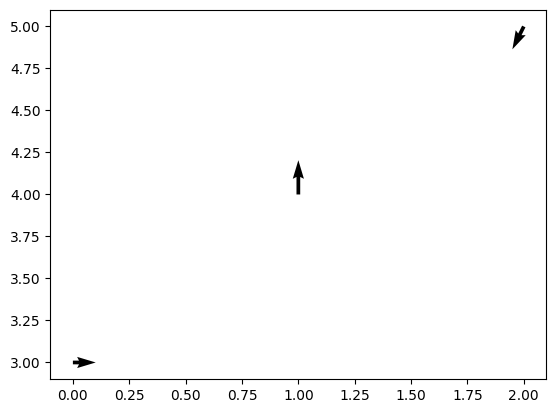
まず，matplotlibモジュールの quiver は，ベクトル場を可視化する関数である．例えば，3つのベクトル \[ \vec{p}_0=\begin{pmatrix}2\\ 0 \end{pmatrix},\quad \vec{p}_1=\begin{pmatrix}0\\ 3 \end{pmatrix},\quad \vec{p}_2=\begin{pmatrix}-1\\ -2 \end{pmatrix} \] を，それぞれ， \[ \mathrm{A}_0=(0,3),\quad \mathrm{A}_1=(1,4),\quad \mathrm{A}_2=(2,5)\] を始点にして描画する場合には，次のIn[15]のようにする．

In [15]:  
x = [0, 1, 2] # A_jのx成分
y = [3, 4, 5] # A_jのy成分

u = [2, 0, -1] # p_jのx成分
v = [0, 3, -2] # p_jのy成分

plt.quiver(x, y, u, v)
plt.show()

次に，一般に，配列 $\mbox{u}=(u_0,u_1,\ldots,u_{n})$ に対して， $\mbox{u[-1]}$ で最後（最後尾）の成分 $u_{n}$ が参照される． $\mbox{u[-2]}$ はその一つ手前 $u_{n-1}$ である．さらに， $\mbox{u[:-1]}=(u_0,\ldots,u_{n-1})$ であり， $\mbox{u[1:]}=(u_1,\ldots,u_{n})$ を意味する．したがって， \[ \mbox{u[1:]}-\mbox{u[:-1]} = \left( u_1-u_0,\ldots,u_{n}-u_{n-1}\right) \] となる． この表記は，配列のサイズがわからない時に便利である．（u.shape[0]で取得できるが、、、）

In [16]:  
u=np.array([1,2,3,4,5])
print(u[-1])
print(u[-2])
print(u[0])
print(u[:-1])
print(u[1:])
print(u[1:]-u[:-1])

Out [16]: 
5
4
1
[1 2 3 4]
[2 3 4 5]
[1 1 1 1]

さらに， \[ \mbox{R}=\begin{pmatrix} x_{0} & y_{0} &z_{0} &w_{0} \\ x_{1} & y_{1} &z_{1} &w_{1} \\ x_{2} & y_{2} &z_{2} &w_{2} \end{pmatrix} \] に対して， \[ \mbox{R[:,0]}= (x_0,x_1,x_2),\quad \mbox{R[:-1,0]}= (x_0,x_1),\quad \mbox{R[1:,0]}= (x_1,x_2),\quad \mbox{R[1:,0]$-$R[:-1,0]}= (x_1-x_0,x_2-x_1), \] そして， \begin{gather*} \mbox{R[:-1,:]} = \begin{pmatrix} x_0 & y_0 & z_0 & w_0 \\ x_1 & y_1& z_1 & w_1 \end{pmatrix} ,\quad \mbox{R[1:,:]}= \begin{pmatrix} x_1 & y_1 & z_1 & w_1 \\ x_2 & y_2 & z_2 & w_2 \end{pmatrix} ,\\ \mbox{R[1:,:]$-$R[:-1,:]}= \begin{pmatrix} x_1-x_0 & y_1-y_0 & z_1-z_0 & w_1-w_0 \\ x_2-x_1 & y_2-y_1 & z_2-z_1 & w_2-w_1 \end{pmatrix} \end{gather*} と計算できる．

In [17]:  
R=np.array([[1,2,3,4],[5,6,7,8],[3,4,5,6]])
print(R)
print(R[:,0])
print(R[:-1,0])
print(R[1:,0])
print(R[1:,0]-R[:-1,0])
print(R[:-1,:])
print(R[1:,:])
print(R[1:,:]-R[:-1,:])

Out [17]: 
[[1 2 3 4]
 [5 6 7 8]
 [3 4 5 6]]
[1 5 3]
[1 5]
[5 3]
[ 4 -2]
[[1 2 3 4]
 [5 6 7 8]]
[[5 6 7 8]
 [3 4 5 6]]
[[ 4  4  4  4]
 [-2 -2 -2 -2]]

さて，いま，2変数のNewton法により，反復列が \[ \mbox{xvect}= \begin{pmatrix} x_0 &y_0\\ x_1 &y_1\\ \vdots & \vdots\\ x_n &y_n \end{pmatrix} \] の形で得られているとしよう．$\mathrm{P}_k=(x_k,y_k)$ とおくとき，$k=0,\ldots,n-1$ に対して，$\mathrm{P}_k$ を始点として，ベクトル $\overrightarrow{\mathrm{P}_k\mathrm{P}_{k+1}}$ を描画したい．上の説明により， \begin{gather*} \mbox{yvect$=$xvect[1:,:] $-$ xvect[:-1,:]}= \begin{pmatrix} x_1-x_0 &y_1-y_0\\ x_2-x_1 &y_2-y_1\\ \vdots & \vdots\\ x_n-x_{n-1} &y_n-y_{n-1} \end{pmatrix} , \\ \mbox{yvect[:,0]}= (x_1-x_0, x_2-x_1, \ldots, x_n-x_{n-1}),\quad \mbox{yvect[:,1]}= (y_1-y_0, y_2-y_1, \ldots, y_n-y_{n-1}) , \\ \mbox{xvect[:-1,0]}= (x_0, x_1, \ldots, x_{n-1}),\quad \mbox{xvect[:-1,1]}= (y_0, y_1, \ldots, y_{n-1}) \end{gather*} である．これを，quiverで描画するようにしたものが，In[13]の，関数newton_drawである．

注意．pythonでは，1次元の配列に対して，「縦($n\times 1$)」、「横($1\times n$)」という区別はないので，なるべく「横」で表記している．それ以上の深い意味はない．

代数方程式の解法

$n$ 次の代数方程式 \begin{align*} f(z) &=z^n+c_1z^{n-1}+c_2z^{n-2}+\cdots+c_{n-1}z+c_n\\ &=(z-a_1)(z-a_2)\cdots(z-a_n)=0\\ \end{align*} の $n$ 個の複素根 $a_1,\ldots,a_n$ を数値的に求める．ただし， $z\in\mathbb{C}$，$c_1,\ldots,c_n\in \mathbb{C}$ としている．$i$ は虚数単位をあらわす．もちろん，与えられた $c_1,\ldots,c_n$ に対して，$a_1,\ldots,a_n$ を求める問題を考えている．

まずは，複素ニュートン法 \[ z_{k+1}=z_{k}-\frac{f(z_{k})}{f'(z_{k})} \] の適用が考えられる．ただし，$f'(z)$ は複素変数 $z$ に関する微分を表す． （この方法は，実は，$\operatorname{Re}f(z)=0,~\operatorname{Im}f(z)=0$という連立方程式に対するNewton法と一致する．）もし，求めたい根 $a$ に対して，十分良い近似値がわかっていれば，それを初期値 $z_0$ とすれば良い． ある近似根 $a$ が求まったら，$f(z)/(z-a)$ に対して，再び複素ニュートン法を適用すれば良い．

$z_0$に関する情報があらかじめ利用できない場合や， すべての解を同時に計算したい場合はどうしたら良いであろうか．それを考える ため，まずは， \[ f'(a_j)=\prod_{l\ne j}(a_j-a_l) \] と言う関係に着目しよう．もし，$a_1,\ldots,a_n$ に対する十分良い近似値 $z_1,\ldots,z_n$ が得られているならば，$\displaystyle{\prod_{l\ne j}(z_j-z_l)}$は，$f'(a_j)$の十分良い近似値になっていることが期待できる． したがって，すべての根を同時に求める趣旨で，反復列$z^{(k)}=(z_1^{(k)},\ldots,z_n^{(k)})$を， \begin{equation} \tag{DK} {z^{(k+1)}_j=z^{(k)}_j -\frac{f(z^{(k)}_j)}{\displaystyle{\prod_{l\ne j}(z^{(k)}_j-z^{(k)}_l)}} \qquad (j=1,\ldots,n)} \end{equation} で生成する．これを，デュラン(Durand)・ケルナー(Kerner)法，あるいは連立法と言う．

この方法は，実は，$f(z)=0$ について根と係数の関係を適用した際に得られる $n$ 個の（実変数・実数値の）連立方程式に，Newton法を適用したものに他ならない．したがって， 重根がなければ，2次収束する．詳しくは，[杉原・室田]の5.2節や[山本]の5.5節を参照せよ．

初期値 $z^{(0)}=(z_1^{(0)},\ldots,z_n^{(0)})$ の選び方については，いろいろな考え方がある．$n$ 個の根 $a_1,\ldots,a_n$ を含むような複素平面上の円盤 $|z-\beta|\le r$ を構成し，円周上を等分割した点 \[ z_j^{(0)}=\beta+r\exp\left[i\left(\frac{2\pi(j-1)}{n}+\gamma\right)\right]\quad (j=1,\ldots,n) \] を採用することが多い．これを，Aberthの方法と言う．$\gamma$ は適当な実数である．これは，$\gamma=0$ だと，必ず $z_1^{(0)}=0$ となってしまうのを避けるために付加するだけであり，それ以上 の意味はない．

さて，(DK)の右辺の分数の分母を計算するために，予備的な考察をしておく．

In [18]:  
z= np.array([1, 2, 3, 4])
print(z.reshape(-1,1))
print(z.reshape(-1,1).shape)
print(z.reshape(1,-1))
print(z.reshape(1,-1).shape)
w=z.reshape(-1,1)-z.reshape(1,-1)+np.eye(4,4)
print(w)
val0=np.prod(w, axis = 0)
val1=np.prod(w, axis = 1)
print(val0)
print(val1)

Out [18]: 
[[1]
 [2]
 [3]
 [4]]
(4, 1)
[[1 2 3 4]]
(1, 4)
[[ 1. -1. -2. -3.]
 [ 1.  1. -1. -2.]
 [ 2.  1.  1. -1.]
 [ 3.  2.  1.  1.]]
[ 6. -2.  2. -6.]
[-6.  2. -2.  6.]

np.arrayで生成した配列 z は，あくまで，1次元配列である（上で述べたように，縦ベクトル，横ベクトルの区別はない）．これを， reshape(-1,1)によって $4\times 1$ の2次元配列として， reshape(1,-1)によって $1\times 4$ の2次元配列として扱う．

次に，numpyでは，例えば，$\boldsymbol{z}=\begin{pmatrix}z_1\\z_2\\z_3\end{pmatrix}$に対して， \[ \boldsymbol{z}-\boldsymbol{z}^{\mathrm{\scriptsize T}} =\begin{pmatrix} 0 & z_1-z_2 & z_1-z_3 \\ z_2-z_1 & 0 & z_2-z_3\\ z_3-z_1 & z_3-z_2 & 0 \end{pmatrix} \] と計算される（$\boldsymbol{z}^{\mathrm{\scriptsize T}}$ は $\boldsymbol{z}$ の転置を表す）．すなわち，行列 $\boldsymbol{z}^{(k)}-(\boldsymbol{z}^{(k)})^{\mathrm{\scriptsize T}}+I$ の第 $j$ 行のすべての成分の積がちょうど $\displaystyle{\prod_{l\ne j}(z_j^{(k)}-z_l^{(k)})}$ となる（$l$ と $j$ の役割に注意せよ）． 積を計算するには，prod(A, axis=1) を利用すれば良い．これは，行列 $A$ の各行の成分の積を成分とする1次元配列を返す．ちなみに，prod(A, axis=0) は，行列 $A$ の各列の積を成分とする1次元配列を返す．

以上を踏まえると，(DK)を実行する関数durand_kernerは，例えば，次のようになる．ついでに，解を可視化する関数draw_solも作っておこう．

In [19]:  
def durand_kerner(f, n, beta, r, maxiter, eps):
  # Aberth の方法による初期値の設定
  gamma=1.7
  t = np.linspace(0,n-1,n)
  z = beta+r*np.exp(1.0j*(2*np.pi*t/n+gamma))
  # Newton iteration
  iter = 0
  zvect = np.array([z])
  f_val = f(z)
  err = np.linalg.norm(f_val, ord=np.inf)
  while err > eps and iter < maxiter:
    df_val = np.prod(z.reshape(-1,1) - z.reshape(1, -1) + np.eye(n,n) , axis=1)
    if np.linalg.norm(df_val, ord=np.inf)<1.0e-15:
      print('denominator is almost zero')
      sys.exit(1)
    z -= f_val / df_val
    f_val = f(z)
    err = np.linalg.norm(f_val, ord=np.inf)
    iter += 1
    zvect = np.vstack((zvect,z))
  return zvect, iter

def draw_sol(xx, n, beta, r, xsol):
  t = np.linspace(0,2*np.pi,200)
  xi = beta+r*np.exp(1.0j*t)
  plt.plot(xi.real, xi.imag,'c--')
  for i in range(n):
    plt.plot(xx[:,i].real, xx[:,i].imag,'bo')
  plt.plot(xsol.real, xsol.imag,'rx', ms=10)
  plt.grid('on')
  plt.gca().set_aspect('equal', adjustable='box') # set aspect ratio as 1:1
  plt.show()
  return 0

例題を作っておこう．$-2\pm i,~3+2i,~1,~2$ を根とする $5$ 次方程式を考える．（プログラムが動くかどうかをチェックするための例題なので，因数分解された形をそのまま用いても良いが，それでは，気分が出ないので．）

In [20]:  
import sympy
sympy.var('z')
a1=-2+1j
a2=-2-1j
a3=3+2j
a4=1
a5=2
f=sympy.expand((z-a1)*(z-a2)*(z-a3)*(z-a4)*(z-a5))
print(f)

Out [20]: 
z**5 - 2.0*z**4 - 2.0*I*z**4 - 8.0*z**3 - 2.0*I*z**3 + 8.0*z**2 + 10.0*I*z**2 + 31.0*z + 14.0*I*z - 30.0 - 20.0*I

実際に実行してみよう．$\beta$ と $r$ は，あまり深く考えずに，$\beta=0$，$r=8$ としてみた（これでうまくいくという保証はない）．

In [21]:  
def f(x):
    return x**5.0-x**4.0*(2.0+2.0j)-x**3.0*(8.0+2.0j)+x**2*(8.0+10.0j)+x*(31.0+14.0j) - (30.0+20.0j)

n=5
beta=0.0
r=8.0
zvect, iter = durand_kerner(f, n, beta, r, 20, 1.0e-12)
zsol=np.array([-2.0+1.0j, -2-1.0j, 1.0, 2.0, 3.0+2.0j])
draw_sol(zvect, n, beta, r, zsol)
print(iter)
for i in range(n):
  print(zvect[iter,i])

Out [21]: 
12
(1-7.323549018766331e-19j)
(-2+1j)
(-2-1j)
(2-5.979667038052334e-17j)
(3.0000000000000004+2.0000000000000004j)

問題

1. 上記の入力と出力をすべて確かめよ．
2. 上の例題で，初期値，$\mathrm{eps}$の値などを変えて，計算を再試行せよ．
3. 例題を自分で設定して，上記の方法を試せ．

課題

課題3.1

$m$ をあらかじめ定めておくパラメータとして，反復列を \begin{equation} \tag{mN} x_{k+1}=x_k-m\frac{f(x_k)}{f'(x_k)}\qquad (k\ge 0) \end{equation} で生成する方法を修正Newton法と言う． これを実行するプログラムとその収束の速さを調べるプログラムを作成せよ． その上で，方程式 $f(x)=x^3-x^2-8x+12=0$ の重根 $a=2$ を求める際に， 修正Newton法の反復列が $a=2$ に2次収束するような $m$ を実験的に求めよ． また，その $m$ で反復列が2次収束することを数学的に説明せよ．

課題3.2

$f(x)$ を滑らかな関数とする．$\xi(\ne x)$ が $x$ に十分近ければ，微分係数 $f'(x)$ の値は， $\frac{f(x)-f(\xi)}{x-\xi}$ で十分よく近似できる．したがって，Newton法では必須であった導関数の計算を避けるために， \begin{equation} \tag{S} x_{k+1}=x_k-f(x_k) \frac{x_k-x_{k-1}}{f(x_k)-f(x_{k-1})}\qquad (k\ge 1) \end{equation} という反復法を考えることができる．これを，セカント法，あるいは，割線法と言う．これは，反復列を生成するために，初期値として $x_0$ と $x_1$ が必要である．これを実行するプログラムとその収束の速さを調べるプログラムを作成せよ．自分で例題を設定して，特に，収束の速さについて調べよ．（もし，可能ならそれを数学的に説明せよ．）

課題3.3

関数 $f(x)=\cosh x+\cos x-2$ を考える． 方程式 $f(x)=0$ には，唯一の解 $a=0$ が存在することを示せ． この方程式にNewton法を適用した際に2次収束が観察できないことを実験的に確かめよ． また，この方程式に修正Newton法を適用した際に，最も収束が速くなる$m$，すなわち，(3.3)において $p$ が最も大きくなる $m$ を実験的に求めて，理由を数学的に説明せよ．

課題3.4

次の関数の最小値（の非常い良い近似値）をNewton法を応用して求めよ． \[ f(x,y)=\frac{2}{5}-\frac{1}{10}(5x^2+5y^2+3xy-x-2y)e^{-(x^2+y^2)},\quad (x,y)\in \mathbb{R}^2. \] （何をNewton法で解けば良いのであろうか？）

課題3.5

「代数方程式の解法」のIn[21]では，多項式の具体形を直接計算することで，多項式の値を計算している．ホーナー(Horner)法について調べ，この部分を，多項式の次数と係数のみを与えて，多項式の値を計算するように修正せよ．また，Aberth の方法による初期値の設定において，方程式に応じて，$\beta$ と $r$ を，うまく選ぶ方法を考えて，例題で試すことで，その妥当性（あるいは非妥当性）を検討せよ（[齊藤2017]の1.6節や[伊理・藤野]の第11章が参考になる．ただし，他の方法もある）．

参考文献など

• [齊藤2012] 齊藤宣一，数値解析入門，東京大学出版会，2012年
• [齊藤2017] 齊藤宣一，数値解析（共立講座数学探求），共立出版，2017年
• [杉原・室田] 杉原正顕，室田一雄，数値計算法の数理，岩波書店，1994年
• [山本] 山本哲朗，数値解析入門[増訂版]，サイエンス社，2003年
• [伊理・藤野]伊理正夫，藤野和建，数値計算の常識，共立出版，1985年