松井 千尋

東京大学大学院 数理科学研究科

新着情報

研究内容

　　　　
　　　　

概要

物質の構成要素である分子や原子など、とても小さい物理的対象は量子力学にしたがって振舞うことが知られています。
量子力学にしたがうミクロな世界の時間発展は、エネルギーに対応する演算子であるハミルトニアンによって定まります。
このため、ハミルトンの固有値および固有状態を求めることで、量子系の振舞いを理解することができます。この操作を、「量子模型を解く」と言います。
多粒子量子模型を解くことは一般に困難ですが、いくつかの模型 (特に一次元系) は厳密に解けることが知られています。解ける模型の背後には共通する数理構造があり、大まかには「多体散乱を2体の散乱に分解したとき、得られる結果は分解のしかたによらない」という性質だと解釈することができます (図1)。この数理構造を用いることで、量子模型の様々な物理的性質を厳密に調べることができます。
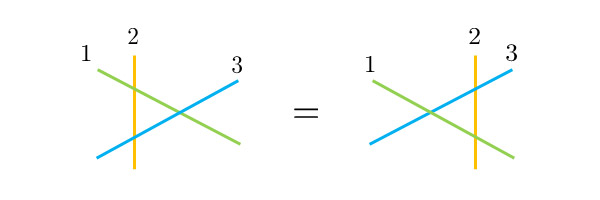
図1. 厳密に解ける模型の多くはヤン・バクスター方程式と呼ばれる，3体散乱に関する代数関係式を満たすことが知られている．これは，2体散乱に分解したときに得られる結果が，分解の仕方によらないことを保証している

図1. 厳密に解ける模型の多くはヤン・バクスター方程式と呼ばれる、3体散乱に関する代数関係式を満たすことが知られている。これは、2体散乱に分解したときに得られる結果が、分解の仕方によらないことを保証している。



これまでの研究対象

これまでの研究対象は、

などです。



可積分高次スピン鎖の相関関数

電子スピンは+1/2あるいは-1/2を取りますが、鉄錯体のような化合物ではより高次のスピン値が現れることがあります。このような化合物がもつスピンを一次元に配置した系を高次スピン鎖とよびます。高次スピン鎖に特殊な形の相互作用項を入れると、可積分系となることが知られており、量子逆散乱法を適用してさまざまな物理量を計算することができます。可積分なS=1/2スピン鎖と同じ代数構造をもつ任意スピンSのスピン鎖において、相関関数をベーテ仮設法を用いて計算しました。S=1/2のときと同様、任意のスピンSに対しても相関関数が行列式表示できることを示しました。このことは、相関関数の行列式表示が代数構造に由来すると解釈することができます。



可積分格子模型における隠れた超対称性

量子場の理論における散乱過程は、光円錐を離散化することによりスピン鎖の転送行列で記述することができます (図2)。互いに対応関係にある場の理論とスピン鎖は赤外極限で同じ散乱行列をもち、また紫外極限では同じ共形場理論によって記述されることが知られています。しかしながら、場の理論で見られる超対称性が、対応するスピン鎖では陽にあらわれません。この問題に対し、無限鎖における物理的な励起状態を考えることで、格子上で超対称性が定義できること、及びそれが場の理論における超対称性と全く同じ代数関係式を満たすことを示しました。


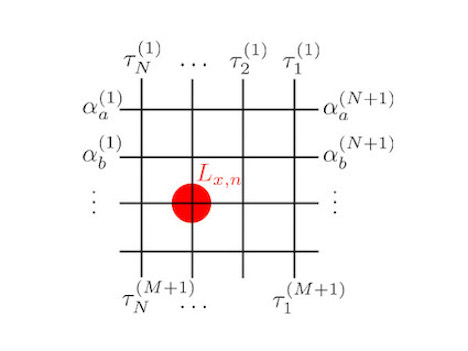
図2. 転送行列は，ある時刻での量子系の状態を次の時刻における状態へと変化させる．可積分量子系では，ある代数関係式を満たす行列Lによって転送行列が構成される．量子場の理論では，光円錐を時間・座標ともに離散化することで，散乱を起こす多粒子状態の時間発展を転送行列で記述できる

図2. 転送行列は、ある時刻での量子系の状態を次の時刻における状態へと変化させる。可積分量子系では、ある代数関係式を満たす行列Lによって転送行列が構成される。量子場の理論では、光円錐を時間・座標ともに離散化することで、散乱を起こす多粒子状態の時間発展を転送行列で記述できる。



可解な定常状態をもつ多状態マルコフ過程

非対称単純排他過程 (ASEP) は離散空間・連続時間上で定義される一次元確率過程です。各サイトは、粒子の有無に応じた2つの状態を取ることができます。このモデルの時間発展はマルコフ行列によって決定され、マルコフ行列のもつ代数構造を通して可積分スピン鎖のハミルトニアンと対応関係にあることが示されています。
マルコフ行列の数学的性質を利用し、1つのサイトが2粒子以上占有できる多状態への拡張を行いました (図3)。多状態への拡張によって定常状態の可解性は保たれる一方、マルコフ行列そのものの可積分性は失われることを示しました。得られた模型の遷移率は、完全非対称極限では同時に遷移する粒子数のみに依存する独立パラメータへと単純化されることがわかりました。


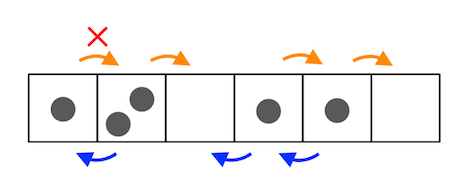
図3. 多状態の非対称単純排他過程では，各サイトにおける粒子数が決まった値（ここでは2個）を超えない範囲で粒子は一つ隣のサイトに遷移することができる．粒子が一方向のみに遷移する完全非対称極限では，遷移率は同時に遷移する粒子の個数のみに依存する

図3. 多状態の非対称単純排他過程では、各サイトにおける粒子数が決まった値 (ここでは2個) を超えない範囲で粒子は一つ隣のサイトに遷移することができる。粒子が一方向のみに遷移する完全非対称極限では、遷移率は同時に遷移する粒子の個数のみに依存する。



可解な定常状態をもつ開放量子系

平衡系と比べ、非平衡系を解析的に調べることは、例え厳密手法でなくてもかなり困難です。一方で近年、Lindblad方程式にしたがって時間発展する開放量子系 (図4) について、厳密に求まる固有モードの存在が注目を集めています。その中でも、バルク部分のハミルトニアンの可解性に起因する部分的に可解なLiouvillianを構成しました。これは、後述する部分的に可解な孤立系を開放系へ拡張したものと解釈できると期待しています。


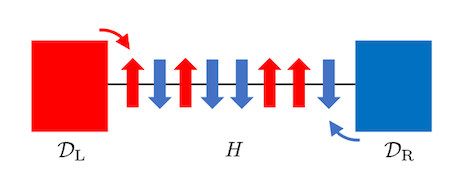
図4. 両端でスピン流の散逸が起こる開放量子系の一例。システムのハミルトニアンと散逸をうまく選ぶと定常状態が厳密に解ける。これは、部分可解な開放量子系の一つと考えられる。

図4. 両端でスピン流の散逸が起こる開放量子系の一例。システムのハミルトニアンと散逸をうまく選ぶと定常状態が厳密に解ける。これは、部分可解な開放量子系の一つと考えられる。



部分的に可解な量子系

量子可積分系では、高い対称性に由来する多くの保存量によって緩和プロセスが強く制限されることにより、熱平衡化しないことが知られています。一方で、系全体が非可積分であっても、特定の部分空間の中の状態が熱平衡化しないような場合が注目を集めています (図5)。この現象を説明するために様々なメカニズムが提唱されていますが、非可積分な模型の中に可積分模型を埋め込むことでその一例が構成できることを示しました。今後は、保存量に着目することで、部分可解性が生じるメカニズムを解明することを目標としています。


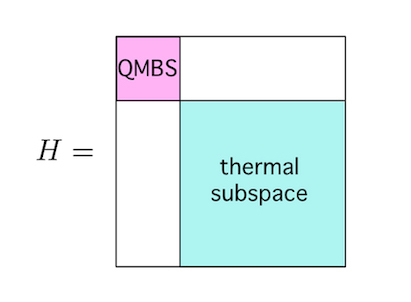
図5. 小さな不変部分空間をもつハミルトニアンでは、マクロに見て熱平衡状態とは異なるエネルギー固有状態がしばしば出現する。この不変部分空間で可解性をもつハミルトニアンが多く見つかっている。

図5. 小さな不変部分空間をもつハミルトニアンでは、マクロに見て熱平衡状態とは異なるエネルギー固有状態がしばしば出現する。この不変部分空間で可解性をもつハミルトニアンが多く見つかっている。

雑誌論文 · 会議録 · 学会発表

　 　　　　　　　 　　　　　　　　　 　　　　　　　　 　　　　　　　 　　　　　　　 　 　　　　　　　　 　　　　　　　 　　　　　　
雑誌論文
　　
    　　　　　　　　　　
      　　　　　　　　
    1. Boundary dissipative spin chains with partial solvability inherited from system Hamiltonians
      Chihiro Matsui and Naoto Tsuji
      arXiv:2409.03208
      2. 　　　　　　　　
    2. Exactly solvable subspaces of non-integrable spin chains with boundaries and quasiparticle interactions
      Chihiro Matsui
      Phys. Rev. B 109, 104307 (2024). arXiv:2309.13911
      3. 　　　　　　　　
    3. Exact steady states of the impurity-doped XXZ spin chain coupled to dissipators
      Chihiro Matsui and Naoto Tsuji
      J. Stat. Mech. : Theor. Exp. 2024, 033105 (2024). arXiv: 2303.17084
      4. 　　　　　　　　
    4. Nonequilibrium physics in integrable systems and spin-flip non-invariant conserved quantities
      Chihiro Matsui
      J. Phys. A: Math. Theor. 53, 134001 (2020). arXiv:2002.01069
      5. 　　　　　　　　
    5. Construction of the steady state density matrix and quasilocal charges for the spin-1/2 XXZ chain with boundary magnetic fields
      Chihiro Matsui and Tomaž Prosen
      J. Phys. A: Math. Theor. 50, 385201 (2017). arXiv:1705.09105
      6. 　　　　　　　　
    6. Spinon excitations in the spin-1 XXZ chain and hidden supersymmetry
      Chihiro Matsui
      Nucl. Phys. B913, 15-33 (2016). arXiv:1607.04317
      7. 　　　　　　　　
    7. A power-law decay model with autocorrelation for posting data to social networking services
      Toshifumi Fujiyama, Chihiro Matsui, and Akimichi Takemura
      PLoS ONE 11(8) (2016). arXiv:1411.2309
      8. 　　　　　　　　
    8. Phase coexistence phenomena in an extreme case of the misanthrope process with open boundaries
      Chikashi Arita and Chihiro Matsui
      Europhys. Lett. 114, 60012 (2016). arXiv:1605.00917
      9. 　　　　　　　　
    9. Multi-state asymmetric simple exclusion processes
      Chihiro Matsui
      J. Stat. Phys. 158, 158-191 (2015). arXiv:1311.7473
      10. 　　　　　　　　
    10. Boundary effects on the supersymmetric sine-Gordon model through light-cone approach
      Chihiro Matsui
      Nucl. Phys. B885, 373-408 (2014). arXiv:1404.3809
      11. 　　　　　　　　
    11. Correlation functions of the integrable higher-spin XXX and XXZ spin chains through the fusion method
      Tetsuo Deguchi and Chihiro Matsui
      Nucl. Phys. B831, 359-407 (2010). arXiv:0907.0582
      12. 　　　　　　　　
    12. Form factors of integrable higher-spin XXZ chains and the affine quantum-group symmetry
      Tetsuo Deguchi and Chihiro Matsui
      Nucl. Phys. B814, 405-438 (2009). arXiv:0807.1847
      13. 　　　　　　　　　　
　
　　　　　
　 　　　　　　　 　　　　　　　　　 　　　　　　　　 　　　　　　　 　　　　　　　 　 　　　　　　　　 　　　　　　　 　　　　　　
会議録，その他
　　
    　　　　　　　　　　
      　　　　　　　　　　　
    1. 窓から見える風景
      松井 千尋
      数理科学6月号; 75-81 (2024).
      2. 　　　　　　　　　　　
    2. Boundary Effects on the Supersymmetric Sine-Gordon Model Through Light-Cone Lattice Regularization
      Chihiro Matsui
      Springer Proceedings in Mathematics & Statistics 191; 311-335 (2016).
      3. 　　　　　　　　　　　
    3. Algebraic aspects of the correlation functions of the integrable higher-spin XXZ spin chains with arbitrary entries
      Tetsuo Deguchi and Chihiro Matsui
      New Trends in Quantum Integrable Systems: Proceedings of the Infinite Analysis 09; 11-33 (2010). arXiv:1005.0888
      4. 　　　　　　　　　　
　
　　　　　
　 　　　　　　　 　　　　　　　　　 　　　　　　　　 　　　　　　　 　　　　　　　 　 　　　　　　　　 　　　　　　　 　　　　　　
学会発表
　　
    　　　　　　　　　　
      　　　　　　　　　　　
    1. A variety of partially solvable models: From closed spin chains to open spin chains (招待講演)
      Chihiro Matsui*
      Mathematics and Physics of Integrability (MPI2024)
      MATRIX (Creswick, Australia); 2024/07/01-19
      2. 　　　　　　　　　　　
    2. Partial solvability and related physical phenomena (基調講演)
      Chihiro Matsui*
      ANZAMP Meetings 2024 (Katoomba, Australia); 2024/02/07-09
      3. 　　　　　　　　　　　
    3. 境界付き非可積分量子スピン鎖における可解な部分空間 (口頭発表)
      松井千尋*
      日本物理学会 第78回年次大会
      東北大学 (宮城); 2023/09/16-19
      4. 　　　　　　　　　　　
    4. Exact steady state of the impurity-doped XXZ spin chain coupled to dissipators (招待講演)
      Chihiro Matsui*
      Workshop on exactly solvable models of open quantum systems
      Steklov Mathematical Institute (Moscow, Russia); 2023/09/11-15
      5. 　　　　　　　　　　　
    5. Exactly solvable subspaces of spin-1 chains with boundaries and quasiparticle interactions (口頭発表)
      Chihiro Matsui*
      10th Bologna Workshop on Conformal Field Theory and Integrable Models
      University of Bologna (Bologna, Italy); 2023/09/04-07
      6. 　　　　　　　　　　　
    6. Steady state of the impurity-doped XXZ spin chain coupled to dissipators (口頭発表)
      Chihiro Matsui*, Naoto Tsuji
      STATPHYS28
      The University of Tokyo (Tokyo, Japan); 2023/08/07-11
      7. 　　　　　　　　　　　
    7. Analysis of the steady state of the impurity-doped XXZ spin chain coupled to dissipators (招待講演)
      Chihiro Matsui*, Naoto Tsuji
      New Frontiers in Integrability
      Trinity College Dublin (Dublin, Ireland); 2023/06/13-16
      8. 　　　　　　　　　　　
    8. Thermalization and relaxation of isolated quantum systems (招待講演)
      Chihiro Matsui*
      Women at the Intersection of Mathematics and Theoretical Physics Meet in Okinawa
      OIST (Okinawa, Japan); 2023/03/20-24
      9. 　　　　　　　　　　　
    9. 不純物を含む散逸付きXXZ鎖の定常状態の解析 (口頭発表)
      松井千尋*, 辻直人
      日本物理学会 2022年秋季大会
      東京工業大学 (東京); 2022/09/12-15
      10. 　　　　　　　　　　　
    10. Quasilocal charges of the XXZ spin chain and integrability of the boundary-driven diffusive system (招待講演)
      Chihiro Matsui*
      Integrable Quantum Many-Body Systems
      Physikzentrum Bad Honnef (Bad Honnef, Germany); 2022/03/23-27
      11. 　　　　　　　　　　　
    11. Nonequilibrium physics of the XXZ model and spin-flip non-invariant conserved quantities (招待講演)
      Chihiro Matsui*
      RIGOROUS STATISTICAL MECHANICS AND RELATED TOPICS II
      Online workshop; 2020/11/24-27
      12. 　　　　　　　　　　　
    12. Nonequilibrium physics in integrable systems and spin-flip non-invariant conserved quantities (招待講演)
      Chihiro Matsui*
      BAXTER2020: FRONTIERS IN INTEGRABILITY
      The Australian National University (Canberra, Australia); 2020/02/11-14
      13. 　　　　　　　　　　　
    13. XXZスピン鎖におけるスピン反転不変性をもたない保存量と非平衡現象 (口頭発表)
      松井千尋*
      日本物理学会2019年秋季大会
      岐阜大学 (岐阜, 岐阜); 2019/09/10-13
      14. 　　　　　　　　　　　
    14. Non-Hermitian quasilocal charges and non-equilibrium behavior of the XXZ model (招待講演)
      Chihiro Matsui*
      International Workshop: Theoretical Developments and Experimental Progresses in Quantum Matter: Dynamics of Quantum Magnetism
      Tsung-Dao Lee Institute (Shanghai, China); 2019/08/26-30
      15. 　　　　　　　　　　　
    15. Nonequilibrium physics in the XXZ model and spin-flip asymmetric conserved quantities (ポスター発表)
      Chihiro Matsui*
      Statphys27
      Edificio San Jose UCA (Buenos Aires, Argentina); 2019/07/08-12
      16. 　　　　　　　　　　　
    16. 可積分系における保存量の準局所性と非平衡現象 (口頭発表)
      松井千尋*
      日本物理学会2018年秋季大会
      同志社大学 (京田辺, 京都); 2018/09/09-12
      17. 　　　　　　　　　　　
    17. Quasilocal charges and non-equilibrium behavior in integrable systems (招待講演)
      Chihiro Matsui*
      Correlations in Integrable Quantum Many-Body Systems
      Wuppertal University (Wuppertal, Germany); 2018/09/03-07
      18. 　　　　　　　　　　　
    18. Quasilocal chargers of the XXZ spin chain and integrability of the boundary-driven diffusive system (招待講演)
      Chihiro Matsui*
      Non-Equilibrium Systems and Special Functions
      MATRIX (Creswick, Australia); 2018/01/08-02/02
      19. 　　　　　　　　　　　
    19. Nature of Symmetry (ポスター発表)
      松井千尋*
      日加先端科学(JCFoS)シンポジウム
      沖縄科学技術大学院大学 (那覇，沖縄); 2017/11/02-05
      20. 　　　　　　　　　　　
    20. Exact solvability of the boundary driven diffusive spin-1/2 XXZ chain with non-diagonal boundary magnetic fields (口頭発表)
      Chihiro Matsui*
      YITP Workshop "Quantum Thermodynamics: Thermalization and Fluctuations"
      Kyoto University (Kyoto); 2017/09/27-30
      21. 　　　　　　　　　　　
    21. 非対角境界磁場付き境界散逸スピン1/2XXZ鎖の可解性 (口頭発表)
      松井千尋*, Tomaž Prosen
      日本物理学会 2017年秋季大会
      岩手大学 (盛岡); 2017/09/21-24
      22. 　　　　　　　　　　　
    22. Hidden supersymmetry behind the Fateev-Zamolodchikov spin chain (招待講演)
      Chihiro Matsui*
      Fall 2017 Chern-Simons Workshop "Integrability across mathematics and physics"
      UC Berkeley (Berkeley, US); 2017/09/13-15
      23. 　　　　　　　　　　　
    23. Exact solvability of the boundary driven diffusive spin-1/2 XXZ chain with non-diagonal boundary magnetic fields (口頭発表)
      Chihiro Matsui*
      Workshop on Classical and Quantum Integrable Systems
      Bogoliubov Laboratory of Theoretical Physics (Dubna, Russia); 2017/07/24-29
      24. 　　　　　　　　　　　
    24. Exact solvability of the boundary driven diffusive spin-1/2 XXZ chain with non-diagonal boundary magnetic fields (招待講演)
      Chihiro Matsui*
      INTEGRABILITY IN LOW-DIMENSIONAL QUANTUM SYSTEMS
      MATRIX (Creswick, Australia); 2017/06/26-07/21
      25. 　　　　　　　　　　　
    25. スピン1XXZ鎖におけるスピノン励起と隠れた超対称性 (口頭発表)
      松井千尋*
      日本物理学会 第72回年次大会
      大阪大学 (大阪); 2017/03/17-20
      26. 　　　　　　　　　　　
    26. 境界付き人嫌い過程における相共存現象 (口頭発表)
      有田親史，松井千尋*
      日本物理学会2016年秋季大会
      金沢大学 (金沢); 2016/09/13-16
      27. 　　　　　　　　　　　
    27. Spinon excitations in the spin-1 XXZ chain and hidden supersymmetry (招待講演)
      Chihiro Matsui*
      New Trends in Low-Dimensional Physics: Quantum Integrability and Applications
      Chinese Academy of Sciences (Beijing, China); 2016/09/01-15
      28. 　　　　　　　　　　　
    28. Multi-state extension of the asymmetric simple exclusion process (口頭発表)
      Chihiro Matsui*
      STATPHYS26
      Centre de Congres de Lyon (Lyon, France); 2016/07/18-22
      29. 　　　　　　　　　　　
    29. Multi-state extension of the asymmetric simple exclusion process (口頭発表)
      Chihiro Matsui*
      Workshop on Classical and Quantum Integrable Systems
      CEuler International Mathematical Institute (St. Petersburg, Russia); 2016/07/11-15
      30. 　　　　　　　　　　　
    30. Multi-state extension of the asymmetric simple exclusion process (招待講演)
      Chihiro Matsui*
      Correlations in Integrable Quantum Many-Body Systems
      Wuppertal University (Wuppertal, Germany); 2016/04/11-14
      31. 　　　　　　　　　　　
    31. 境界付き可積分量子スピン鎖におけるスピノン励起 (口頭発表)
      松井千尋*
      日本物理学会
      東北学院大学 (宮城); 2016/03/19-22
      32. 　　　　　　　　　　　
    32. 可積分高次スピン鎖におけるスピノン励起 (口頭発表)
      松井千尋*
      日本物理学会
      関西大学 (大阪); 2015/09/16-19
      33. 　　　　　　　　　　　
    33. Multi-state extension of the asymmetric simple exclusion processes (口頭発表)
      Chihiro Matsui*
      Integrable systems and quantum symmetries
      Břehová 7 (Prague, Czech); 2015/06/23-27
      34. 　　　　　　　　　　　
    34. Boundary effects on the supersymmetric sine-Gordon model through light-cone regularization (口頭発表)
      Chihiro Matsui*
      XI. International Workshop LIE THEORY AND ITS APPLICATIONS IN PHYSICS
      Pochivna baza BAN (Varna, Bulgaria); 2015/06/15-21
      35. 　　　　　　　　　　　
    35. 可解多状態非対称単純排他過程の構成 (口頭発表)
      松井千尋*
      日本物理学会
      早稲田大学 (東京); 2015/03/21-24
      36. 　　　　　　　　　　　
    36. Boundary effects on the supersymmetric sine-Gordon model through light-cone regularization (招待講演)
      Chihiro Matsui*
      Integrable Lattice Models and Quantum Field Theories
      Physikzentrum Bad Honnef (Bad Honnef, Germany); 2014/06/26-07/02
      37. 　　　　　　　　　　　
    37. 非対称単純排他過程の多状態への拡張 (口頭発表)
      松井千尋*
      日本物理学会
      東海大学 (神奈川); 2014/03/27-30
      38. 　　　　　　　　　　　
    38. Multi-state extension of the asymmetric simple exclusion processes (招待講演)
      Chihiro Matsui*
      New Topics on Stochastic and Quantum Interacting Particle Systems
      The University of Tokyo (Tokyo, Japan); 2013/12/10
      39. 　　　　　　　　　　　
    39. Multi-state Asymmetric Simple Exclusion Processes (ポスター発表)
      Chihiro Matsui*
      The 3rd International Symposium on Innovative Mathematical Modelling
      The University of Tokyo (Tokyo, Japan); 2013/11/12-15
      40. 　　　　　　　　　　　
    40. Superconformal field theory and supersymmetric sine-Gordon model with Dirichlet boundary conditions (招待講演)
      Chihiro Matsui*
      Kavli IPMU Workshop on Gauge and String Theory
      Kavli IPMU (Chiba, Japan); 2013/08/26-09/06
      41. 　　　　　　　　　　　
    41. Superconformal field theory and supersymmetric sine-Gordon model with Dirichlet boundary conditions (口頭発表)
      Chihiro Matsui*
      STATPHYS25
      Seoul National University (Seoul, Korea); 2013/07/22-26
      42. 　　　　　　　　　　　
    42. Superconformal field theory and supersymmetric sine-Gordon model with Dirichlet boundary conditions (招待講演)
      Chihiro Matsui*
      Conformal Field Theory, Integrable Models and Liouville gravity
      Ehwa Womans University (Seoul, Korea); 2013/07/18-20
      43. 　　　　　　　　　　　
    43. Superconformal field theory and supersymmetric sine-Gordon model with Dirichlet boundary conditions (口頭発表)
      Chihiro Matsui*
      Euler Symposium on Theoretical and Mathematical Physics
      Euler Institute (St. Petersburg, Russia); 2013/07/12-17
      44. 　　　　　　　　　　　
    44. 境界磁場のかかった高次スピンハイゼンベルグ鎖の励起状態 (口頭発表)
      松井千尋*
      日本物理学会
      広島大学 (広島); 2013/03/26-29
      45. 　　　　　　　　　　　
    45. ディリクレ境界条件下における超対称サイン · ゴルドン模型に対する非線形積分方程式 (口頭発表)
      松井千尋*
      日本物理学会
      横浜国立大学 (神奈川); 2012/09/11-14
      46. 　　　　　　　　　　　
    46. The ground state of SUSY sine-Gordon model with the Dirichlet boundary conditions via lattice regularization (ポスター発表)
      Chihiro Matsui*
      RAQIS12
      Universite d'Angers (Angers, France); 2012/09/10-14
      47. 　　　　　　　　　　　
    47. 可積分スピン鎖とそれに関連する非平衡モデルについて (ポスター発表)
      松井千尋*
      非平衡系の物理—その普遍的理解を目指して
      京都大学 (京都); 2012/08/01-04
      48. 　　　　　　　　　　　
    48. Boundary Effect on the 19-vertex Model (ポスター発表)
      Chihiro Matsui*
      The 2nd International Symposium om Innovative Mathematical Modelling
      The University of Tokyo (Tokyo, Japan); 2012/05/15-18
      49. 　　　　　　　　　　　
    49. 超対称サイン・ゴルドン模型における境界束縛状態 (口頭発表)
      松井千尋*
      日本物理学会
      富山大学 (富山); 2011/09/21-24
      50. 　　　　　　　　　　　
    50. Boundary bound states in spin-1 XXZ model and SUSY sine-Gordon model with Dirichlet boundaries (ポスター発表)
      Chihiro Matsui*
      CFT ANDINTEGRABLE MODELS
      University of Bologna (Bologna, Italy); 2011/09/12-15
      51. 　　　　　　　　　　　
    51. Boundary bound states in spin-1 XXZ model and SUSY sine-Gordon model with Dirichlet boundaries (口頭発表)
      Chihiro Matsui*
      Correlation Functions of Quantum Integrable Models
      Institut de Mathematiques de Bourgogne (Dijon, France); 2011/09/07-09
      52. 　　　　　　　　　　　
    52. Boundary bound states in spin-1 XXZ model and SUSY sine-Gordon model with Dirichlet boundaries (ポスター発表)
      Chihiro Matsui*
      Workshop on Integrability and its Breaking in Strongly Correlated and Disordered Systems
      SISSA (Trieste, Italy) 2011/05/23-27
      53. 　　　　　　　　　　　
    53. The ground state of the integrable spin-s XXZ spin chain with boundaries (ポスター発表)
      Chihiro Matsui*
      DMQS2010
      The University of Tokyo (Tokyo, Japan); 2011/02/14-16
      54. 　　　　　　　　　　　
    54. 境界付き可積分XXZ高次スピン鎖の基底状態 (口頭発表)
      松井千尋*
      非線形数理若手の会
      九州大学西新プラザ (福岡); 2010/11/15-17
      55. 　　　　　　　　　　　
    55. 境界付き可積分XXZ高次スピン鎖における相関関数 (口頭発表)
      松井千尋*
      日本物理学会
      大阪府立大学 (大阪); 2010/09/23-26
      56. 　　　　　　　　　　　
    56. Correlation functions of integrable spin chains with boundaries (口頭発表)
      Chihiro Matsui*
      StatPhys24
      Cains Convention Centre (Cains, Australia); 2010/07/19-23
      57. 　　　　　　　　　　　
    57. Correlation functions of integrable spin chains with boundaries (口頭発表)
      Chihiro Matsui*
      Finite-Size Techlnology in Low-Dimensional Quantum Systems (V)
      Centro de Ciencias de Benasque Pedro Pascual (Benasque, Spain); 2010/06/27-07/19
      58. 　　　　　　　　　　　
    58. Correlation functions of integrable spin chains with boundaries (口頭発表)
      Chihiro Matsui*
      RAQIS10
      LAPTH (Annecy, France); 2010/06/15-18
      59. 　　　　　　　　　　　
    59. Correlation functions of integrable spin chains with boundaries (口頭発表)
      Chihiro Matsui*
      Days on Diffraction
      PDMI (St. Petersburg, Russia); 2010/06/08-11
      60. 　　　　　　　　　　　
    60. Central charge of alternating integrable spin chains (ポスター発表)
      Chihiro Matsui*
      2010 International Symposium on Physics of Quantum Technology
      Hitotsubashi Memorial Hall (Tokyo, Japan); 2010/04/06-09
      61. 　　　　　　　　　　　
    61. 可解高次スピンXXZ鎖の任意の相関関数:ギャップレスの場合 (口頭発表)
      出口哲生*, 松井千尋
      日本数学会無限可積分系セッション
      慶応大学 (神奈川); 2010/03/24-28
      62. 　　　　　　　　　　　
    62. テンソル積空間中の既約部分空間に対するUq(sl2)代数の作用について (口頭発表)
      松井千尋*, Andrei G. Bytsko
      日本物理学会
      岡山大学 (岡山); 2010/03/20-23
      63. 　　　　　　　　　　　
    63. Correlation functions for higher spin integrable systems (ポスター発表)
      Chihiro Matsui*
      Condensed Matter Physics Meets High Energy Physics
      IPMU (Chiba, Japan); 2010/02/08-12
      64. 　　　　　　　　　　　
    64. 転送行列における補助空間の状態数による量子系ハミルトニアンの制御 (口頭発表)
      松井千尋*, 宮下精二
      日本物理学会
      熊本大学 (熊本); 2009/09/25-28
      65. 　　　　　　　　　　　
    65. Control of Hamiltonians of Quantum Integrable Systems by Classical Integrable Systems (ポスター発表)
      Chihiro Matsui*, Seiji Miyashita
      Infinite Analysis 09
      Kyoto University (Kyoto, Japan); 2009/07/27-31
      66. 　　　　　　　　　　　
    66. 可積分高次スピンXXZ鎖の形状因子に対する二つの公式 (口頭発表)
      出口哲生*, 松井千尋
      日本物理学会
      立教大学 (東京); 2009/03/27-30
      67. 　　　　　　　　　　　
    67. A relation between integrable models of quantum and classical statistical mechanics (招待講演)
      Chihiro Matsui*, Tetsuo Deguchi, Seiji Miyashita
      Conformal Field Theory, Integrable Models and Liouville gravity
      Landau Institute (Chernogolovka, Russia); 2009/06/27-07/02
      68. 　　　　　　　　　　　
    68. 可積分高次スピンXXZ鎖の形状因子に対する二つの公式 (口頭発表)
      出口哲生*, 松井千尋
      日本物理学会
      立教大学 (東京); 2009/03/27-30
      69. 　　　　　　　　　　　
    69. Correlation functions of integrable higher-spin XXZ chains and the quantum inverse scattering problem (口頭発表)
      松井千尋*, 出口哲生
      日本数学会秋季総合分科会無限可積分系セッション
      東京工業大学 (神奈川); 2008/09/24-27
      70. 　　　　　　　　　　　
    70. 可解高次スピンXXZ鎖の相関関数 (口頭発表)
      松井千尋*, 出口哲生
      日本物理学会
      岩手大学 (岩手); 2008/09/20-23
      71. 　　　　　　　　　　　
    71. 可積分高次スピンXXZ鎖における量子逆散乱 (口頭発表)
      松井千尋*, 出口哲生
      日本物理学会
      岩手大学 (岩手); 2008/09/20-23
      72. 　　　　　　　　　　
　
　　　　　

授業担当科目

　 　　　　　　　 　　　　　　　　　 　 　 　　　　　　　　 　 　 　　　　　　　　 　　　　　　　　　 　 　 　　　　　　　　 　 　 　　　　　　　　 　　　　　　　　　 　 　 　　　　　　　　 　 　 　　　　　　　　 　　　　　　　　　 　 　 　　　　　　　　 　 　 　　　　　　　　 　　　　　　　　　 　 　 　　　　　　　　 　 　 　　　　　　　　 　　　　　　　　　 　 　 　　　　　　　　 　 　 　　　　　　　　 　　　　　　　 　　　　　　
2024年度Aセメスター微分積分学演習
現象数理III / 数理解析学概論
応用数学XC / 数物先端科学VIII / 数理解析学概論
Sセメスター学術フロンティア講義
数理科学基礎演習 / 数学基礎理論演習
現象数理II / 現象数理学 / 非線型数理
2023年度Aセメスター線型代数学②
現象数理III / 数理解析学概論
応用数学XC / 数物先端科学VIII / 数理解析学概論
数学特別講究
Sセメスター数理科学基礎 / 線型代数学①
現象数理II / 現象数理学 / 非線型数理
数学講究XB
2022年度Aセメスター線型代数学演習
微分積分学演習
現象数理III / 数理解析学概論
応用数学XC / 数物先端科学VIII / 数理解析学概論
数学特別講究
Sセメスター数理科学基礎演習 / 数学基礎理論演習
現象数理II / 現象数理学 / 非線型数理
数学講究XB
2020年度Aセメスター線型代数学演習
線型代数学②
現象数理III / 数理解析学概論
数理情報学
Sセメスター数理科学基礎演習 / 数学基礎理論演習
数理科学基礎 / 線型代数学①
現象数理II / 現象数理学 / 非線型数理
学術フロンティア講義
2019年度Aセメスター線型代数学②
現象数理III / 数理解析学概論
数理情報学
Sセメスター数理科学基礎 / 線型代数学①
現象数理II / 現象数理学 / 非線型数理
2018年度Aセメスター線型代数学演習
現象数理III / 数理解析学概論
数理情報学
Sセメスター数理科学基礎演習 / 数学基礎理論演習
数理科学セミナーI / 物質科学セミナーI
現象数理II / 現象数理学 / 非線型数理

職歴 · 学歴 · 実績

　　　　　　

松井 千尋 - Chihiro MATSUI -

東京大学大学院 数理科学研究科 准教授

    　　　　　　　　　　
  • 2017.04 - 現在
    東京大学大学院数理科学研究科 准教授
    • 　　　　　　　　　　
  • 2013.10 - 2017.03
    東京大学大学院情報理工学系研究科数理情報学専攻 助教
    • 　　　　　　　　　　
  • 2012.04 - 2013.09
    JST FIRST合原最先端数理モデルプロジェクト 研究員
    • 　　　　　　　　　
    　　　　　　　　　　
  • 2012.03
    東京大学大学院理学系研究科物理学専攻 博士課程修了 (指導教官: 宮下精二 教授)
    • 　　　　　　　　　　
  • 2009.03
    東京大学大学院理学系研究科物理学専攻 修士課程修了 (指導教官: 宮下精二 教授)
    • 　　　　　　　　　　
  • 2007.03
    東京大学理学部物理学科 卒業
    • 　　　　　　　　　
    　　
  • 2023-2026 (予定) 基盤研究C (研究代表者)
    非平衡定常状態近傍での量子可積分系の応答および揺らぎに現れる普遍性クラスの解明 (課題番号 23K03244)
    • 　　
  • 2018-2022 若手研究(研究代表者)
    非エルミート保存量を用いた可積分系スピン鎖のダイナミクスの解明 (課題番号 18K13465)
    • 　　
  • 2015-2019 若手研究(B) (研究代表者)
    スピン鎖が持つ自由度とその有効場理論に現れる超対称性との関係の解明 (課題番号 15K20939)
    • 　　
  • 2011-2013 特別研究員奨励費(B) (研究代表者)
    境界付き量子一次元系における臨界現象の研究築 (課題番号 11J10068)
    • 　　　　　　　　　
    　　
  • 2019/07/08-12
    Topic 1 Poster Award (Chihiro Matsui)
    Statphys27 (Buenos Aires, Argentina)
    • 　　
  • 2014/04/23
    NTTコム オンライン賞 (株田達矢, 藤山俊文, 松井千尋, 竹村彰通)
    第一回データビジネス創造コンテスト
    • 　　
  • 2013/11/12-15
    Best Poster Award Bronze Prize; (Chihiro Matsui)
    The 3rd International Symposium on Innovative Mathematical Modelling
    The University of Tokyo (Tokyo, Japan);
    • 　　　　　　　　　

連絡先

住所

〒153-8914
東京都目黒区駒場3-8-1
東京大学大学院 数理科学研究科棟