What's New?
- 2026/06/01-19
Invited talk at "Integrable Dynamics: from Stochastic Evolution to Quantum Dynamics". - 2025/12/12
A new paper "Symmetry-protected topological scar subspaces" has been submitted on arXiv.
Research
Overview
The very small physical entities constituting matter, such as molecules and atoms, behave according to quantum mechanics. The time evolution of the microscopic world governed by quantum mechanics is determined by the Hamiltonian, an operator corresponding to energy.
Therefore, by seeking the eigenvalues and eigenstates of the Hamiltonian, it is possible to understand the behavior of quantum systems. This operation is referred to as "solving the quantum model." While solving many-body quantum models is generally challenging, some models, especially in one-dimensional systems, are known to have exact solutions. Behind these solvable models, there is a common mathematical structure, roughly interpreted as "when decomposing many-body scattering into two-body scatterings, the obtained results are independent of the way of decompositions." (Fig. 1)
By utilizing this mathematical structure, it becomes possible to exactly investigate various physical properties of quantum models.
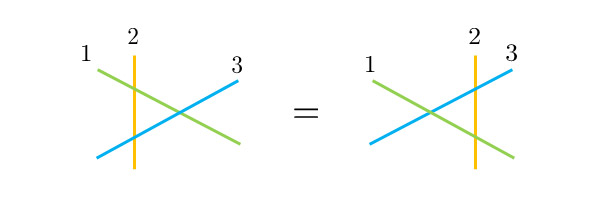
Figure 1. Many models that can be exactly solable are known to satisfy algebraic equations related to three-body scattering, known as the Yang-Baxter equation. This guarantees that the results obtained when decomposing a multi-body scattering into a sequence of two-body scatterings do not depend on the way of decomposition.
Keywords
- Correlation functions of integrable higher-spin chains
- Hidden supersymmetry in integrable lattice models
- Multi-state Markov processes with solvable steady states
- Open quantum systems with solvable steady states
- Partially integrable quantum systems
Correlation functions of integrable higher-spin chains
Electron spins typically take values of +1/2 or -1/2, but in compounds such as iron complexes, higher spin values may occur. Systems where the spins of such compounds are arranged in one dimension are referred to as higher-spin chains. It is known that introducing specific forms of interaction terms in higher-spin chains leads to integrable systems, and various physical quantities can be computed using quantum inverse scattering methods.
In the case of a spin chain with an arbitrary spin S, having the same algebraic structure as an integrable S=1/2 spin chain, we calculated correlation functions using the Bethe ansatz method. Similar to the S=1/2 case, it was demonstrated that correlation functions can be represented in determinant forms for any spin S. This suggests that the determinant expressions of correlation functions originate from the algebraic structure.
Hidden supersymmetry in integrable lattice models
Scattering processes of the quantum field theory can be described by the transfer matrix of the spin chain through the light-cone lattice regularization (Fig. 2). Quantum field theories and quantum spin chains that are in correspondence possess the same scattering matrix in the IR limit and are described by the same conformal field theory in the UV limit. However, the supersymmetry observed in a certain field theory does not explicitly manifest in the corresponding spin chain.
To address this issue, considering the physical excitations in an infinite chain, it has been demonstrated that supersymmetry can be defined on the lattice and satisfies precisely the same algebraic relations as supersymmetry in field theory.
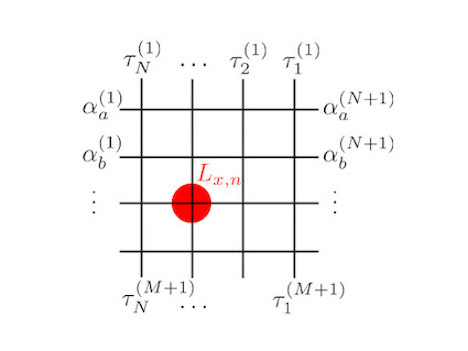
Figure 2. The transfer matrix changes the state of a quantum system at a certain time to the state at the next time. In integrable quantum systems, the transfer matrix is constructed from the L-matrix that satisfies certain algebraic equations. In the quantum field theory, by discretizing the light-cone in both time and space, the time evolution of multiparticle states undergoing scatterings can be described using the transfer matrix.
Multi-state Markov processes with solvable steady states
The Asymmetric Simple Exclusion Process (ASEP) is a one-dimensional stochastic process defined on discrete space and continuous time. Each site can take two states whether vacant or occupied. The time evolution of this model is determined by a Markov matrix, and it has been shown that there is a correspondence between the Markov matrix and the Hamiltonian of an integrable spin chain via their algebraic structure. Utilizing the mathematical properties of the Markov matrix, we generalized the process to a multi-state process, where a single site can be occupied by more than two particles (Fig. 3). While the solvability of the steady state is preserved in this generalization, we showed that the integrability of the Markov matrix itself is lost. The transition rates of the obtained model were found to be simplified to independent parameters, depending only on the number of simultaneously hopping particles, in the fully asymmetric limit (Figure 2).
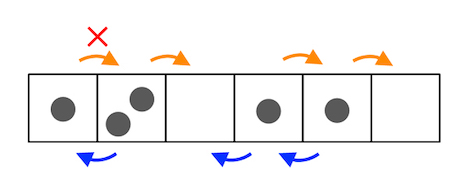
Figure 3. In a multistate asymmetric simple exclusion process, particles can hop from one site to a neighboring site, with the constraint that the number of particles at each site does not exceed a given value (e.g. 2). In the totally asymmetric limit, where particles only transition in one direction, the transition rates depend solely on the number of particles simultaneously hop.
Open quantum systems with solvable steady states
Compared to equilibrium systems, analytically investigating non-equilibrium systems can be quite challenging, even if not using exact methods. However, in recent years, there has been significant interest in the existence of exactly solvable eigenmodes for open quantum systems evolving according to the Lindblad equation (Fig. 4). Specifically, we have constructed partially solvable Liouvillians due to the integrability of the bulk Hamiltonian. It is anticipated that this can be interpreted as an extension of partially solvable isolated systems to open systems, as discussed below.
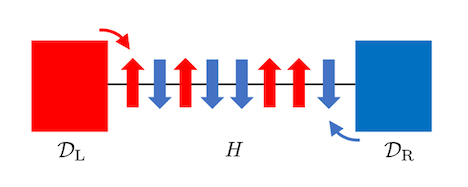
Figure 4. An example of an open quantum system with spin current dissipation occurring at both ends. By carefully choosing the system Hamiltonian and dissipators, the steady state can be exacly solved. This is considered to be one of the partially solvable open quantum systems.
Partially integrable quantum systems
In quantum integrable systems, the absence of thermalization is well-known due to the strong restrictions imposed by many conserved quantities arising from high symmetries. On the other hand, it is of great interests that states within specific subspaces do not thermalize although the entire system is non-integrable (Fig. 5). We have proposed new construction of partially solvable models by embedding an integrable model. The future goal is to elucidate the mechanisms of how partial solvability arises from the viewpoit of conserved quantities.
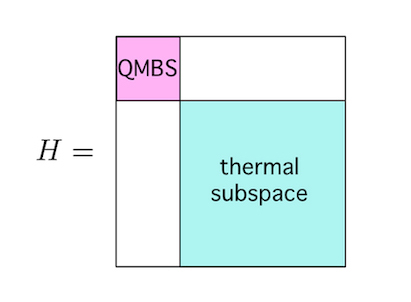
Figure 5. Hamiltonians with small invariant subspaces often exhibit energy eigenstates that differ macroscopically from thermal equilibrium states. It has been discovered that many Hamiltonians are solvable in these small subspaces.
Publications
| Journal Articles |
|---|
|
| Conference Proceedings & Others |
|---|
|
| Conference Presentations |
|---|
|
Lectures
| 2025年度 | Aセメスター | 微分積分学② 現象数理III / 数理解析学概論 応用数学XA / 数物先端科学VIII / 数理解析学概論 数学特別講究 |
|---|---|---|
| Sセメスター | 数理科学基礎 微分積分学① 現象数理II / 現象数理学 / 非線型数理 数学講究XA 数学講究XB |
|
| 2024年度 | Aセメスター | 微分積分学演習 現象数理III / 数理解析学概論 応用数学XC / 数物先端科学VIII / 数理解析学概論 |
| Sセメスター | 学術フロンティア講義 数理科学基礎演習 / 数学基礎理論演習 現象数理II / 現象数理学 / 非線型数理 |
|
| 2023年度 | Aセメスター | 線型代数学② 現象数理III / 数理解析学概論 応用数学XC / 数物先端科学VIII / 数理解析学概論 数学特別講究 |
| Sセメスター | 数理科学基礎 / 線型代数学① 現象数理II / 現象数理学 / 非線型数理 数学講究XB |
|
| 2022年度 | Aセメスター | 線型代数学演習 微分積分学演習 現象数理III / 数理解析学概論 応用数学XC / 数物先端科学VIII / 数理解析学概論 数学特別講究 |
| Sセメスター | 数理科学基礎演習 / 数学基礎理論演習 現象数理II / 現象数理学 / 非線型数理 数学講究XB |
|
| 2020年度 | Aセメスター | 線型代数学演習 線型代数学② 現象数理III / 数理解析学概論 数理情報学 |
| Sセメスター | 数理科学基礎演習 / 数学基礎理論演習 数理科学基礎 / 線型代数学① 現象数理II / 現象数理学 / 非線型数理 学術フロンティア講義 |
|
| 2019年度 | Aセメスター | 線型代数学② 現象数理III / 数理解析学概論 数理情報学 |
| Sセメスター | 数理科学基礎 / 線型代数学① 現象数理II / 現象数理学 / 非線型数理 |
|
| 2018年度 | Aセメスター | 線型代数学演習 現象数理III / 数理解析学概論 数理情報学 |
| Sセメスター | 数理科学基礎演習 / 数学基礎理論演習 数理科学セミナーI / 物質科学セミナーI 現象数理II / 現象数理学 / 非線型数理 |
Curriculum Vitae
Chihiro MATSUI -
Graduate School of Mathematical Sciences, The University of Tokyo (Associate Professor)
- 2017.04 - Present
Graduate School of Mathematical Sciences, The University of Tokyo (Associate Professor) - 2013.10 - 2017.03
Department of Mathematical Informatics, The University of Tokyo (Assistant Professor) - 2012.04 - 2013.09
JST FIRST Aihara Innovative Mathematical Modelling Project (Researcher) - 2011.04 - 2012.03
Research Fellowships for Young Scientists (DC2) - 2009.04 - 2012.03
Ph.D. The University of Tokyo (Supervisor: Prof. Seiji Miyashita) - 2007.04 - 2009.03
M.S. Physics, The University of Tokyo (Supervisor: Prof. Seiji Miyashita) - 2003.04 - 2007.03
B.S. Physics, The University of Tokyo
- 2023-2026 Grant-in-Aid for Scientific Research (C) (Principal Investigator)
Universality classes in responses and fluctuations of quantum integrable systems near non-equilibrium steady states (23K03244) - 2018-2022 Grant-in-Aid for Young Scientists (Principal Investigator)
Dynamics of integrable spin chains via non-Hermitian conserved quantities (18K13465) - 2015-2019 Grant-in-Aid for Young Scientists (B) (Principal Investigator)
Relation between degrees of freedom in spin chains and supersymmetries in their effective field theories (15K20939) - 2011-2013 Grant-in-Aid for JSPS Fellows (Principal Investigator)
Critical phenomena of one-dimensional quantum systems with boundaries (11J10068)
- 2019/07/08-12
Topic 1 Poster Award (Chihiro Matsui)
Statphys27 (Buenos Aires, Argentina) - 2014/04/23
NTTコム オンライン賞 (株田達矢, 藤山俊文, 松井千尋, 竹村彰通)
第一回データビジネス創造コンテスト - 2013/11/12-15
Best Poster Award Bronze Prize; (Chihiro Matsui)
The 3rd International Symposium on Innovative Mathematical Modelling
The University of Tokyo (Tokyo, Japan);
Links
| Research Institutes | The University of Tokyo | https://www.u-tokyo.ac.jp/en/index.html |
|---|---|---|
| Graduate School of Mathematical Sciences, The University of Tokyo | https://www.ms.u-tokyo.ac.jp/index.html | |
| Art Center The University of Tokyo (ACUT) | https://www.art.c.u-tokyo.ac.jp/en/ | |
| Department of Physics, Graduate School of Science, The University of Tokyo | https://www.phys.s.u-tokyo.ac.jp/en/ | |
| Department of Mathematical Informatics, Graduation School of Information Science and Technology, The University of Tokyo | https://www.i.u-tokyo.ac.jp/edu/course/mi/index_e.shtml | |
| Seminars | Departmental colloquia | https://www.ms.u-tokyo.ac.jp/seminar/colloquium_e/index_e.html |
| StatPhys Seminar | https://sites.google.com/view/statphys-seminar | |
| Kavli IPMU Seminars | https://research.ipmu.jp/seminar/?mode=seminar_recent | |
| Outreach Activities | #WeChange UTokyo | https://wechange.adm.u-tokyo.ac.jp/en/ |
| Office for Gender Equality, The University of Tokyo | https://www.u-tokyo.ac.jp/kyodo-sankaku/en/index.html |
Contact
Address
3-8-1, Komaba, Meguro, Tokyo,
Grad. Sch. of Math. Sci. Bldg.
