|
 日程： ２０１７年１月１８日（水）１０：００ 〜 １６：１５
| ||||||||||||
|
場所： 東京大学大学院数理科学研究科棟 002号室
| ||||||||||||
講師（講演順，敬称略）：
| ||||||||||||
 プログラム：
|
1．Matthieu Alfaro 氏： "Long range dispersion vs. Allee effect"
Abstract：
In this talk, we study the balance between long range dispersal kernels and the Allee effect in population dynamics models.
To do so, we first revisit the so called Fujita blow up phenomena [Fujita(1966)] for the nonlocal diffusion equation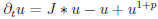 
.
We prove that the Fujita exponent dramatically depends on the behavior of the Fourier transform of the kernel $J$ near the origin, which is linked to the tails of $J$.
Then, as an application of the result in population dynamics models, we discuss the so called hair trigger effect [Aronson-Weinberger(1978)] for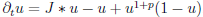 
.
Last, we consider the spreading properties of the above equation. Our interest is twofold: we investigate the existence/non existence of travelling waves, and the propagation properties of the Cauchy problem, more precisely the possibility
of accelaration [Hamel-Roques(2010), Garnier(2011)] during an invasion.
アブストラクトPDF版： Alfaro
2．Xing Liang 氏： "The semi-wave solutions of the KPP equations with free boundaries in almost periodic media"
Abstract：
Consider the following diffusive KPP equation with a free boundary,
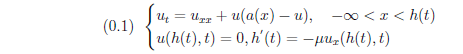
where μ>0, a(x) is a positive alomost periodic function in x∈\R.
Here, as in previous works, we use the concept "semi-wave" to replace "traveling wave" since the profile function of the wave is only defined on the half real line (-∞,0].
Definition
Let (u,h)=(u(x,t),h(t)) be one positive entire solution of (0.1).
If $u$ can be written as u(x,t)=v(x-h(t),h(t)), where h(±∞)=±∞, v(\xi,\tau)∈C^2((-∞,0]×\R),
v(\cdot,\tau) is an almost periodic function in \tau from \R to C((-∞,0])∩L^∞((-∞,0)),
then $u$ is called an almost periodic traveling wave solution.
In my work, I prove the existence and uniqueness of the semi-wave solutions.
アブストラクトPDF版： Liang
3．Gaël Raoul 氏： "Climate change and the impact of a heterogeneous environment"
Abstract：
We consider a natural population facing a climate change.
To survive climate change, a species can change its range, migrating toward colder regions (see [Berestycki-Diekmann-Nagelkerke-Zegeling(2009)].
This is however not the only possible strategy: a species can also change its phenotypes to be able to tolerate higher temperature.
This evolution is the result of mutations and selections (we neglect here more complicated phenomena, such as phenotypic plasticity or sexual reproduction [Kirkpatrick-Barton(1997)].
This evolutionary dynamics are known to play a role at the ecological scale: it is well documented that the phenotypes of a species are not uniform throughout the species range,
and that each individual tends to be adapted to its local environment [Turesson(1922)].
We consider a PDE model, that can be derived as a large population limit of an individual-based model [Champagnat-Méléard(2007)].
In a first study [Alfaro-Berestycki-Raoul, to appear], we show that in linear environments, and in the presence of climate change, the propagation speed can be computed explicitly.
This analysis relies on a careful use of Harnack inequalities. We also try to go beyond this first result: large scale heterogeneities, such as mountains, play an important role in the dynamics of species.
On a few examples, we are able to push the analysis further to provide new ideas in a few biologically relevant situations.
This and the study of multi-dimensional position spaces is a current work also involving biologist Ophélie Ronce.
Finally, I will discuss some ideas to develop an interface dynamics limit that could be useful to link this type of result to presence/absence maps that are used by field biologists working on those questions.
アブストラクトPDF版： Raoul
4．Thomas Giletti 氏： "Spreading and extinction in a multidimensional shifting environment"
Abstract：
In this talk we will consider a heterogeneous reaction-diffusion equation in a multidimensional or cylindrical domain, where the reaction term depends on a moving variable $x-ct$.
More precisely, we study the large time behaviour of solutions of the following Cauchy problem
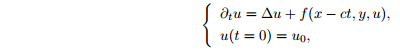
in the spatial domain (x,y)∈\R×ω, where ω⊂\R^{N-1} and N≧1.
Such an equation arises in the modelling of the effect of climate change on species ranges in ecology.
In such a context, the unknown $u$ stands for a population density, and the parameter c>0 stands for the climate velocity in the x-direction (the variable $x$ may correspond for instance to the latitude).
Our key assumptions will be that the reaction term is increasing with respect to $x-ct$, and that the limit of f(x-ct,y,u) as x-ct→+∞ (respectively x-ct→-∞) is a monostable function of $u$
(respectively a negative function of $u$). This means that the favourable habitat zone is receding to the right with a constant speed as time passes.
We will see that, under the joint influence of the heterogeneity and a weak Allee effect,
whether the solution spreads (i.e. converges to a positive steady state which is close to 1 in the favourable zone) depends not only on the shfiting parameter $c$ but also on the size of the initial datum $u_0$.
This is in sharp contrast with both the KPP (no Allee effect) equation in a shifting environment [Berestycki-Diekmann-Nagelkerke-Zegeling(2009)], and with the monostable equation in a homogeneous environment
[Aronson-Weinberger(1978)], where a hair-trigger effect typically appears.
We will further analyze the situation by showing the existence of several sharp thresholds between two reasonable outcomes, namely extinction (i.e. convergence to 0) and spreading of the solution,
in terms of both the climate velocity and the initial datum. This is a joint work with Juliette Bouhours.
アブストラクトPDF版： Giletti
世話人： 俣野博 問い合わせ先： matano
ms.u-tokyo.ac.jp
会場へのアクセスは，
https://www.ms.u-tokyo.ac.jp/access/index.html
にてご確認ください．