2024-3A 数理情報学（東京大学教養学部） [齊藤宣一] [top] [A] [B] [C] [UTOL]

C. 移流方程式とHamilton-Jacobi方程式に対する差分スキーム

線形移流方程式に対する差分スキーム

斉次の線形移流方程式の初期値問題 \begin{align} u_t+cu_x&=0, && (x,t)\in \mathbb{T}\times (0,T),\tag{C.1a}\\ u(x,0)&={a}(x), && x\in \mathbb{T}\tag{C.1b} \end{align} を考える．ただし，$\mathbb{T}=\mathbb{R}/\mathbb{Z}$ としている．

$0 < N,m\in\mathbb{Z}$ を取り，$h=1/N$，$\tau=T/M$， $x_i=ih$，$t_n=n\tau$ とする．$u^n_i\approx u(x_i,t_n)$ が求めるべき近似解である．以下，何も断らなくても， \[ u_{i+N}^n=u_{i}^n \] とする．

(C.1)に対する最も素朴な差分スキームは， \begin{equation*} \frac{u^{n+1}_i-u^n_i}{\tau}+c\frac{u_{i+1}^n-u_{i-1}^n}{2h}=0, \end{equation*} すなわち， \begin{equation} \tag{C.2} \mu \stackrel{\textrm{def.}}{=}c\frac{\tau}{h} \end{equation} とおいて（講義では，$\mu$ を $\lambda$ と書いていたので注意せよ）， \begin{equation} \tag{C.3} u^{n+1}_i=u^n_i-\frac{1}{2}\mu (u_{i+1}^n-u_{i-1}^n) \end{equation} である．これを中心差分スキームと呼ぶ．初期条件は， \begin{equation} \tag{C.4} u^{0}_i={a}(x_i) \end{equation} とする（このことは，以後，いちいち断らない）．

さらに， \begin{equation} \tag{C.5} \lambda \stackrel{\textrm{def.}}{=}|\mu|=|c|\frac{\tau}{h} \end{equation} とおく．

利用予定のモジュールを最初にまとめてインポートしておく．

In [1]:  
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import animation, rc
from IPython.display import HTML

In [2]:  
from google.colab import drive
drive.mount('/content/drive')

可視化のためのプログラムは，前回までと同じものを使う．

In [3]:  
#図のプロット、一枚の図に、グラフを重ねる
def plot_solution(xgrid, uvect):
  # 描画に関するパラメータの設定
  umax = np.max(sol)
  umin = np.min(sol)
  ulength = umax - umin
  umax += 0.05 * ulength
  umin -= 0.05 * ulength
  # t = 0                  
  plt.plot(xgrid,uvect[0,:],color='#ff8c00')
  # t > 0
  for n in range(1,uvect.shape[0]):
    plt.plot(xgrid,uvect[n,:],color='#00bfff')
  
  plt.xlabel('x')
  plt.ylabel('u')
  plt.ylim(umin, umax)
  plt.grid('on')
  plt.show()

In [4]:  
#アニメーションの作成
# IPython.displayモジュールを使う
def plot_animation(xgrid, tgrid, uvect):
  # 描画に関するパラメータの設定
  umax = np.max(sol)
  umin = np.min(sol)
  xmax = np.max(xgrid)
  xmin = np.min(xgrid)
  ulength = umax - umin
  utop = umax + 0.1*ulength
  umax += 0.05*ulength
  umin -= 0.05*ulength
  xmid = (xmax+xmin)/2
  xlength = xmax - xmin
  xmax += 0.05*xlength
  xmin -= 0.05*xlength
  
  # fig, axオブジェクトを作成
  fig, ax = plt.subplots()
  ims = []
  
  # t = 0
  n = 0
  im, = ax.plot(xgrid, uvect[n, :], color='#ff8c00')
  title = ax.text(xmid, utop, f'time={tgrid[n]:.4f}', ha='center', va='center', fontsize=15)
  ims.append([im, title])
    
  # t > 0
  for n in range(1, uvect.shape[0]):
    im, = ax.plot(xgrid, uvect[n, :], color='#00bfff')
    title = ax.text(xmid, utop, f'time={tgrid[n]:.4f}', ha='center', va='center', fontsize=15)
    ims.append([im, title])
    
  # 各軸のラベル
  ax.set_xlabel(r"$x$", fontsize=15)
  ax.set_ylabel(r"$u$", fontsize=15)
  # グラフの範囲を設定
  ax.set_xlim([xmin, xmax])
  ax.set_ylim([umin, umax])
  ax.grid(True)

  # ArtistAnimationにfigオブジェクトとimsを代入してアニメーションを作成
  return animation.ArtistAnimation(fig, ims)

(C.3)を実行するために，次のような In [6] を用意する． In [6] では， $\mathrm{u}=(u_0^n,u_1^n,\ldots,u_{N-1}^n)\in\mathbb{R}^{N}$ に対して， \[ \mathrm{np.roll(u,-1)}=(u_1^n,u_2^n,\ldots,u_{N-1}^n,u_{0}^n),\quad \mathrm{np.roll(u,1)}=(u_{N-1}^n,u_0^n,\ldots,u_{N-2}^n) \] であることを利用して，(C.3)の $u_{i+1}^n-u_{i-1}^n$ の部分を計算している．In [5]を参照せよ．

In [5]:  
N=5
y=np.linspace(0, 1, N+1)
print(y)
print(np.roll(y,-1))
print(np.roll(y,1))

Out [5]: 
[0.  0.2 0.4 0.6 0.8 1. ]
[0.2 0.4 0.6 0.8 1.  0. ]
[1.  0.  0.2 0.4 0.6 0.8]

In [6]:  
#線形移流方程式に対する中心差分スキーム
def linear_advection_central(c, initial, N, T, lam, num):
  L = 1.0
  h = L/N
  tau = lam*h/abs(c)
  mu = c*tau/h
  nmax = int(T/tau)
  step = int(max(1, nmax/num))

  xgrid = np.linspace(0.0, L, N)
  xtmp = np.copy(xgrid[0:N-1])
  tgrid = np.array([0.0])
  u = initial(xtmp)
  sol = np.copy(np.append(u,u[0]))

  for n in range(nmax):
    u = u - 0.5*mu*(np.roll(u,-1)-np.roll(u,1))
    tnow = (n+1)*tau
    if (n+1)%step==0:
      sol=np.vstack((sol,np.append(u,u[0])))
      tgrid=np.append(tgrid, tnow)

  return xgrid, tgrid, sol

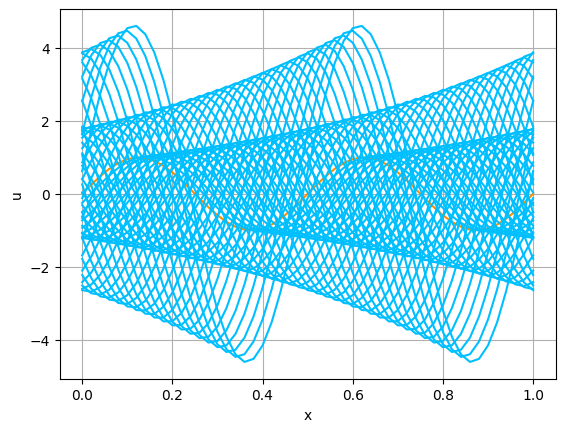
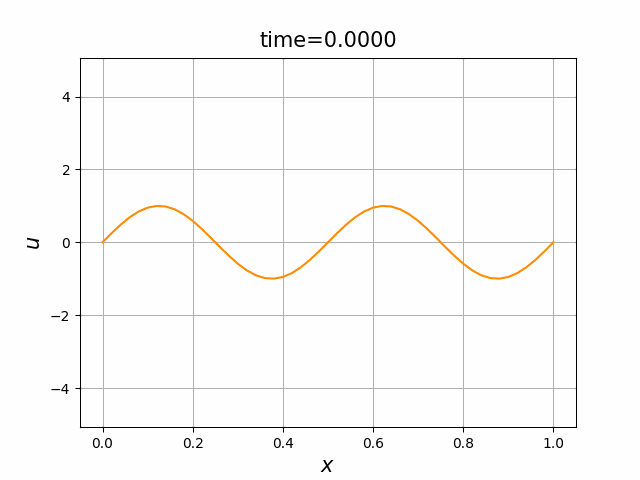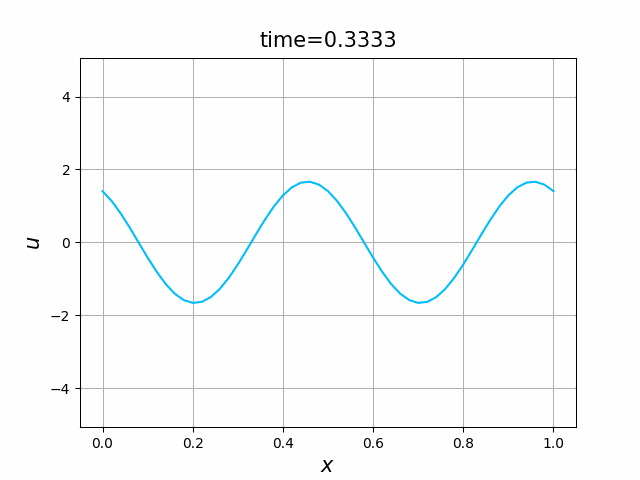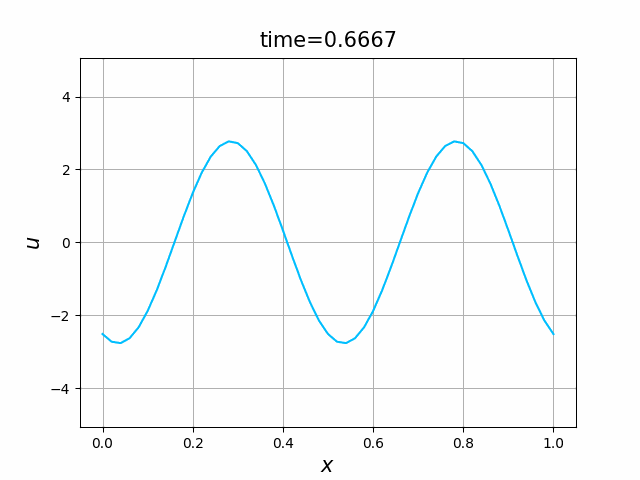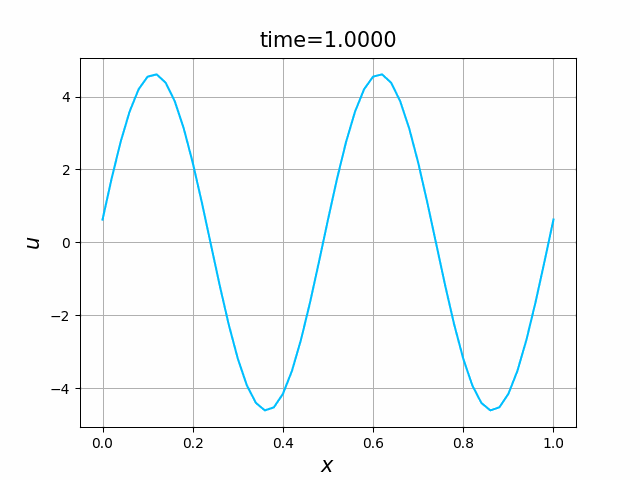
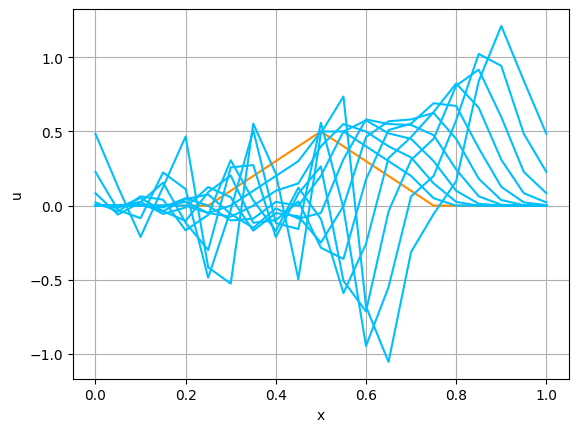
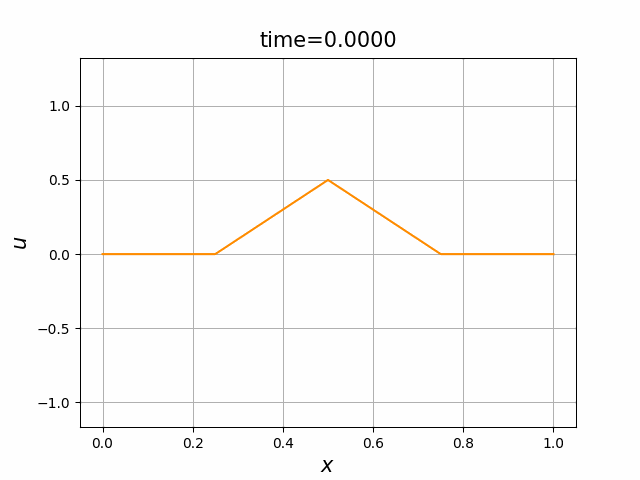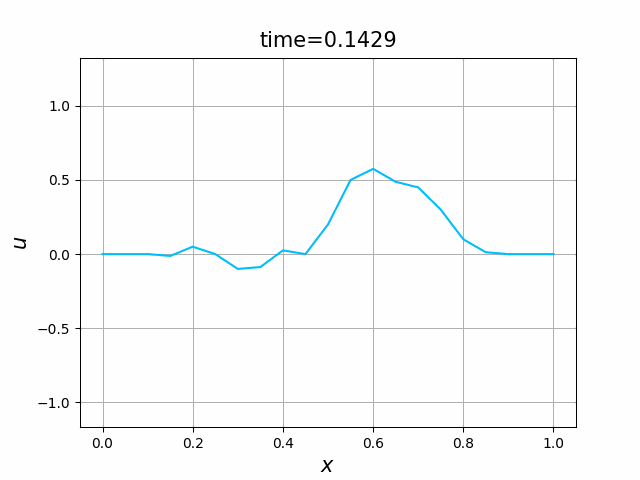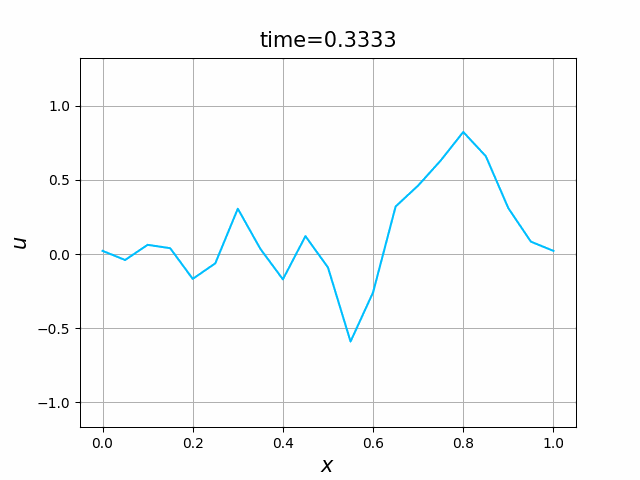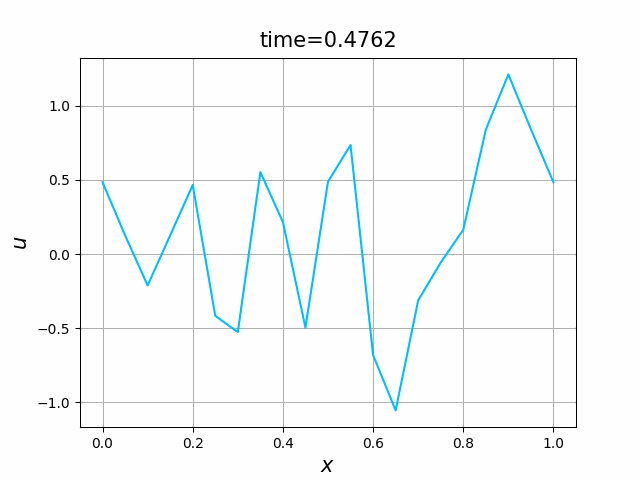
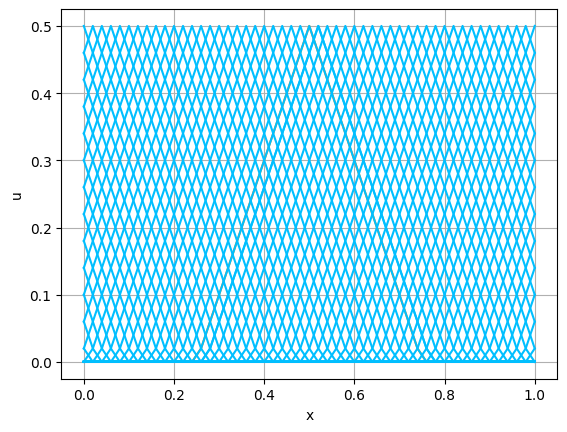
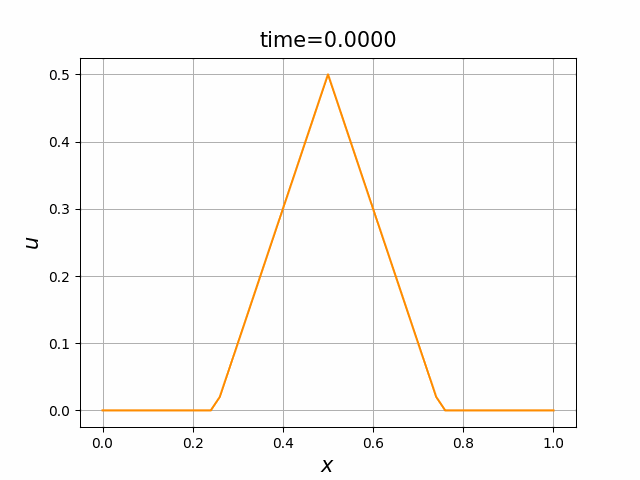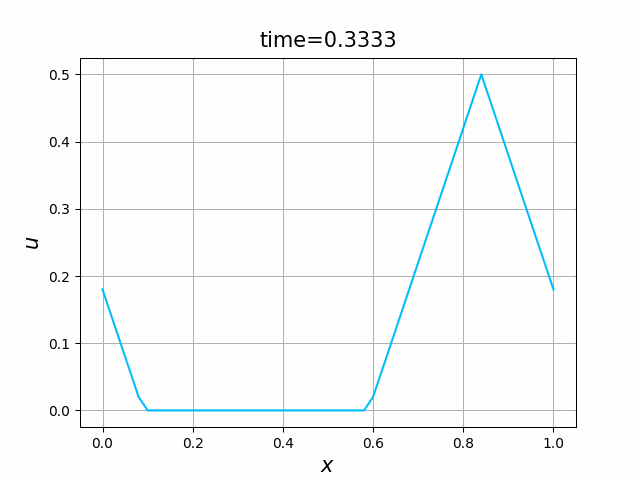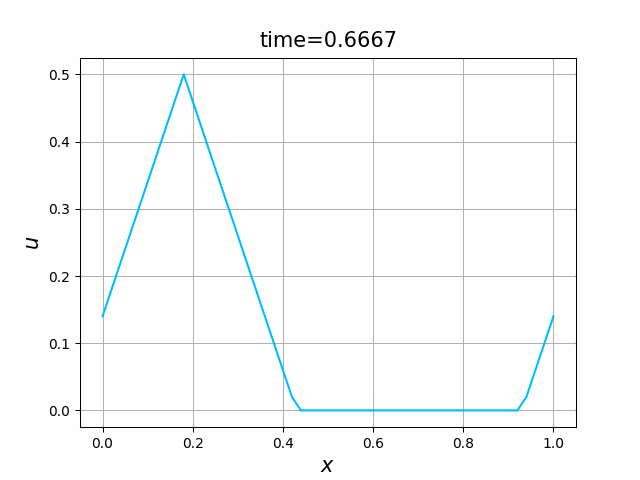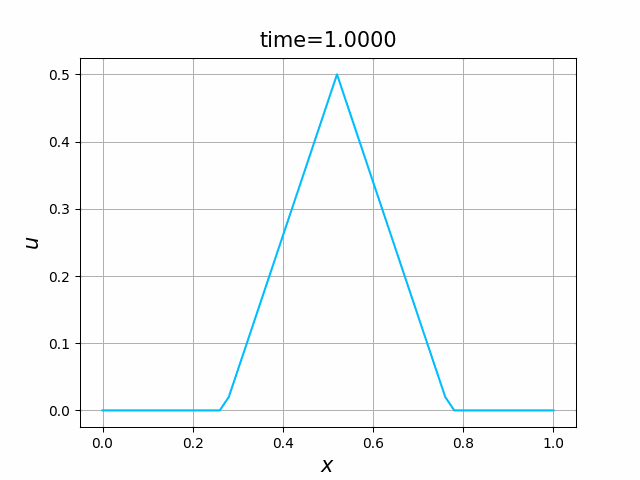
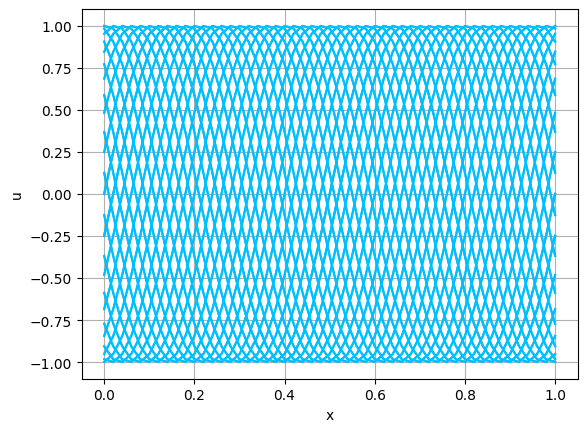
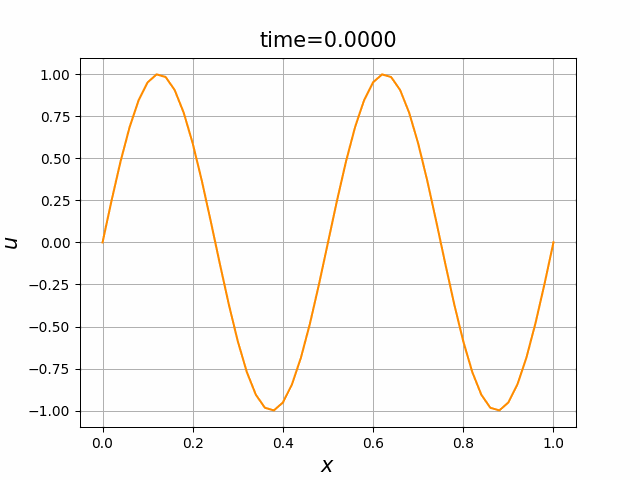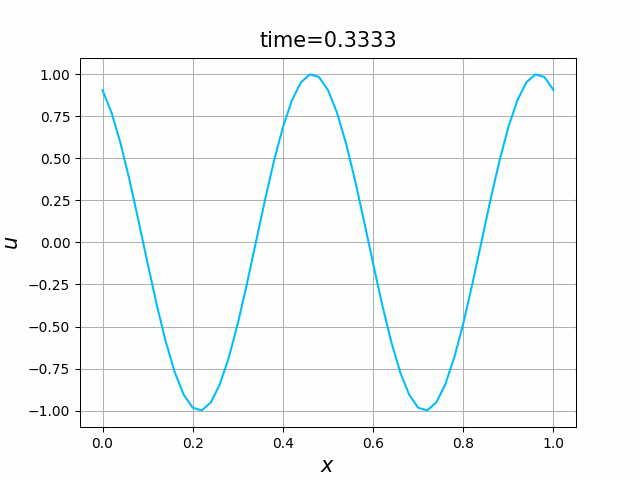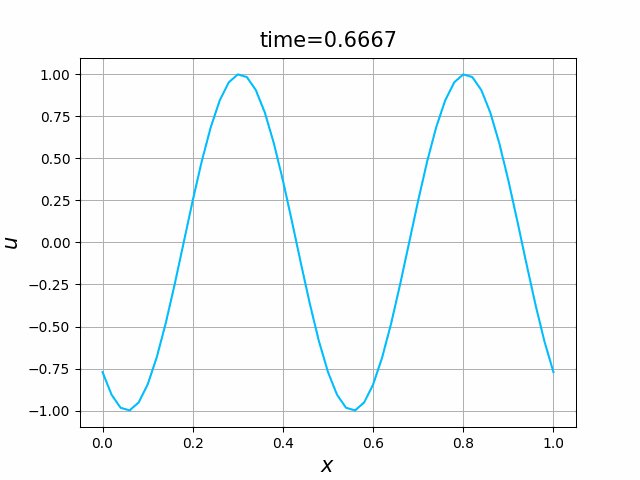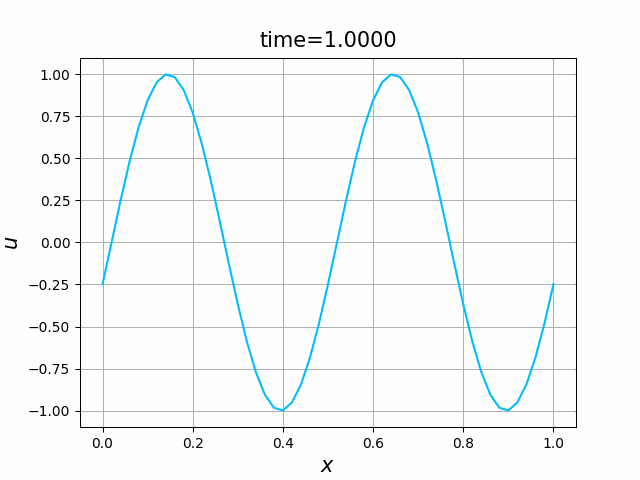
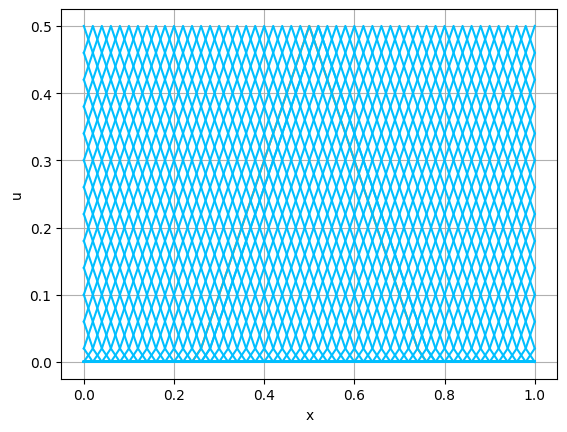
2つの初期関数 \begin{align} a_1(x)&=\sin(4\pi x),\tag{C.6a}\\ a_2(x)&=\max\{ 0, ~ \min\{2x-1/2, 3/2-2x\}\} \tag{C.6b} \end{align} について，In [6] を実行してみる． $c=1$ として $\lambda$ は $\lambda=|c|=1$ とする．図C.1が $a_1$，図C.2が $a_2$ を用いた計算結果である．

In [7]:  
# 初期値
def initial1(x):
  return np.sin(4*np.pi*x)

def initial2(x):
  return  np.maximum(0.0, np.minimum(2.0*x-0.5, 1.5-2.0*x))

#パラメータの設定
c = 1.0
N = 51
T = 1.0
lam = 1
num = 40

#線形移流方程式の計算
x, tn, sol = linear_advection_central(c, initial1, N, T, lam, num)

#図の表示
plot_solution(x, sol)

#アニメーションを表示
anim = plot_animation(x, tn, sol)
#結果をheat.gifに保存（Googleドライブをマウントしておくこと！）
anim.save('/content/drive/MyDrive/Colab Notebooks/fig/heat.gif', writer='pillow')
rc('animation', html='jshtml')
plt.close()
anim

(C.1)に対して，別の差分スキームを考えることができる．まず，$c > 0$ とする．この場合は，(C.1)を， \begin{equation*} \frac{u^{n+1}_i-u^n_i}{\tau}+c\frac{u_{i}^n-u_{i-1}^n}{h}=0, \end{equation*} すなわち， \begin{equation*} u^{n+1}_i=u^n_i-\mu (u_{i}^n-u_{i-1}^n) \end{equation*} と近似する． $c < 0$ の場合は， \begin{equation*} u^{n+1}_i=u^n_i-\mu (u_{i+1}^n-u_{i}^n) \end{equation*} とする．まとめると， \begin{equation} \tag{C.7} u_i^{n+1}= [1-\theta\mu+(1-\theta)\mu] u_i^n +\theta\mu u_{i-1}^n -(1-\theta)\mu u_{i+1}^n,\quad \theta= \begin{cases} 1 &(c\ge 0)\\ 0 &(c< 0) \end{cases} . \end{equation} これを風上（upwind）差分スキームあるいは上流（upstream）差分スキームと呼ぶ．初期条件は，(C.4)と同じである．これを実行するために， In [8] を用意する．

さらに， \begin{equation*} \frac{u^{n+1}_i-\frac{u^n_{i-1}+u^n_{i+1}}{2}}{\tau} +c \frac{u_{i+1}^n-u_{i-1}^n}{2h}=0, \end{equation*} すなわち， \begin{equation} \tag{C.8} u^{n+1}_i=\frac{1+\mu}{2}u^n_{i-1}+\frac{1-\mu}{2}u_{i+1}^n \end{equation} をLax--Friedrichs (LF) 差分スキームと言う．これを実行するために， In [9] を用意する．

In [8]:  
#線形移流方程式に対する風上差分スキーム
def linear_advection_upwind(c, initial, N, T, lam, num):
  L = 1.0
  h = L/N
  tau = lam*h/abs(c)
  nmax = int(T/tau)
  step = int(max(1, nmax/num))
  mu = c*tau/h
  theta = 1 if c >= 0 else 0

  xgrid = np.linspace(0.0, L, N)
  xtmp = np.copy(xgrid[0:N-1])
  tgrid = np.array([0.0])
  u = initial(xtmp)
  sol = np.copy(np.append(u,u[0]))

  for n in range(nmax):
    u = (1.0 - theta*mu + (1.0 - theta)*mu)*u + theta*mu*(np.roll(u,1)) - (1.0 - theta)*mu*(np.roll(u,-1))
    tnow = (n+1)*tau
    if (n+1)%step==0:
      sol=np.vstack((sol,np.append(u,u[0])))
      tgrid=np.append(tgrid, tnow)

  return xgrid, tgrid, sol

In [9]:  
#線形移流方程式に対するLax--Friedrics差分スキーム
def linear_advection_lax(c, initial, N, T, lam, num):
  L = 1.0
  h = L/N
  tau = lam*h/abs(c)
  nmax = int(T/tau)
  step = int(max(1, nmax/num))
  mu = c*tau/h

  xgrid = np.linspace(0.0, L, N)
  xtmp = np.copy(xgrid[0:N-1])
  tgrid = np.array([0.0])
  u = np.vectorize(initial)(xtmp)
  sol = np.copy(np.append(u,u[0]))

  for n in range(nmax):
    u = 0.5*(1.0+mu)*np.roll(u,1) + 0.5*(1.0-mu)*np.roll(u,-1)
    tnow = (n+1)*tau
    if (n+1)%step==0:
      sol=np.vstack((sol,np.append(u,u[0])))
      tgrid=np.append(tgrid, tnow)

  return xgrid, tgrid, sol

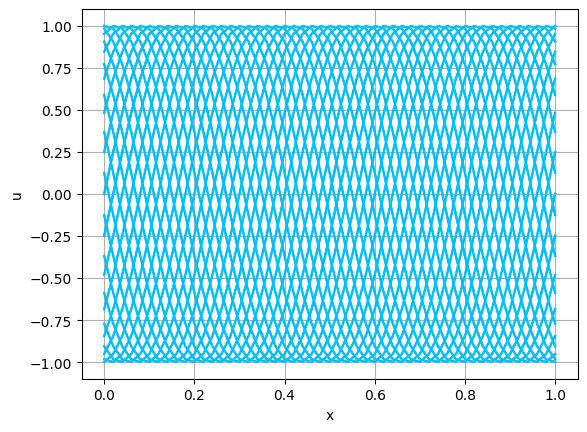
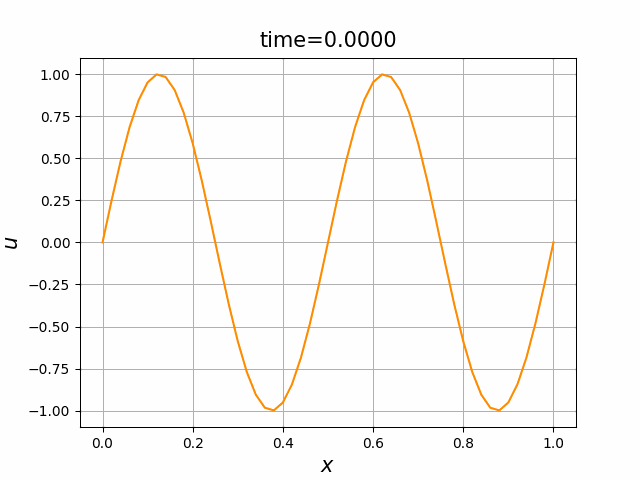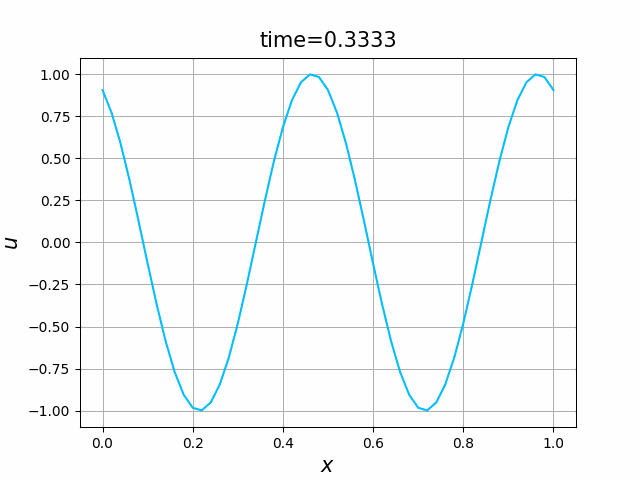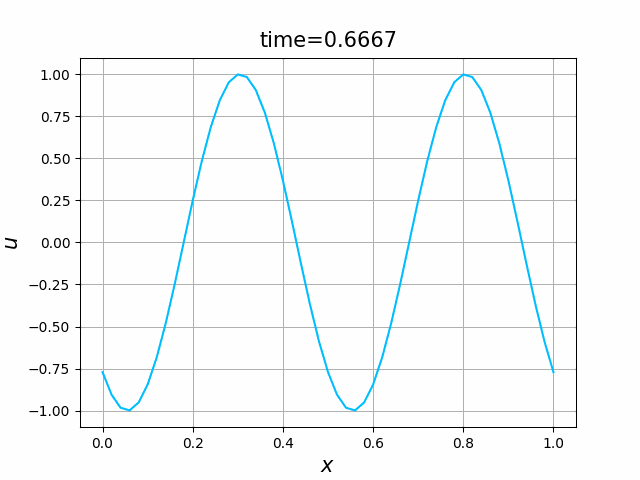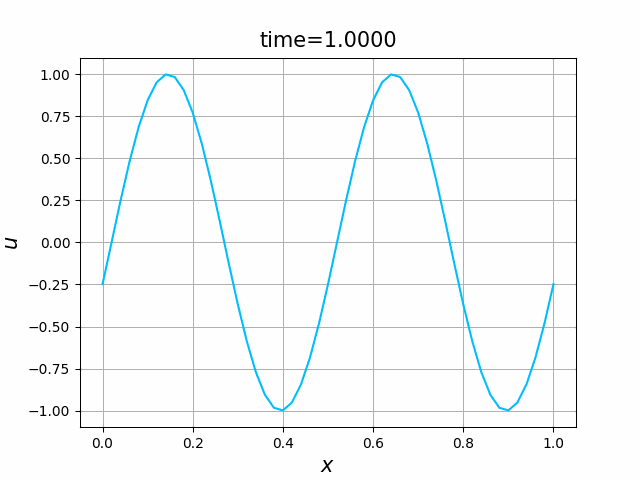
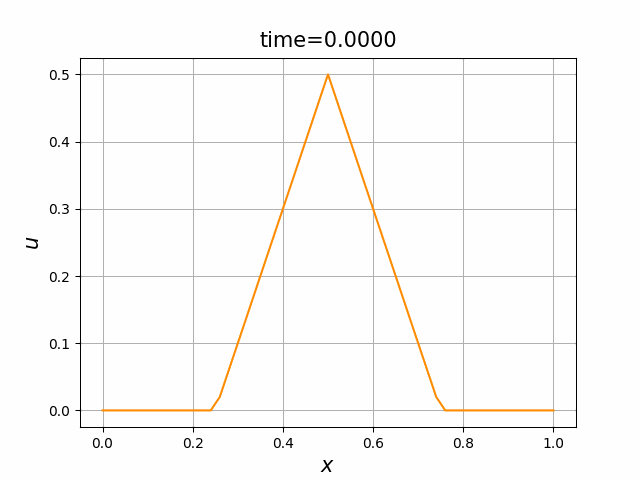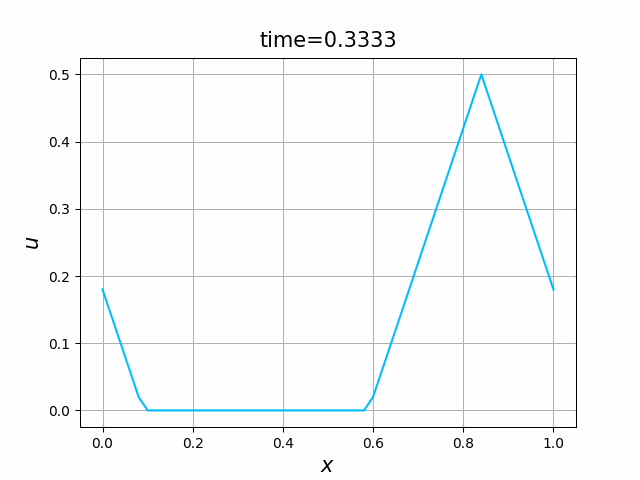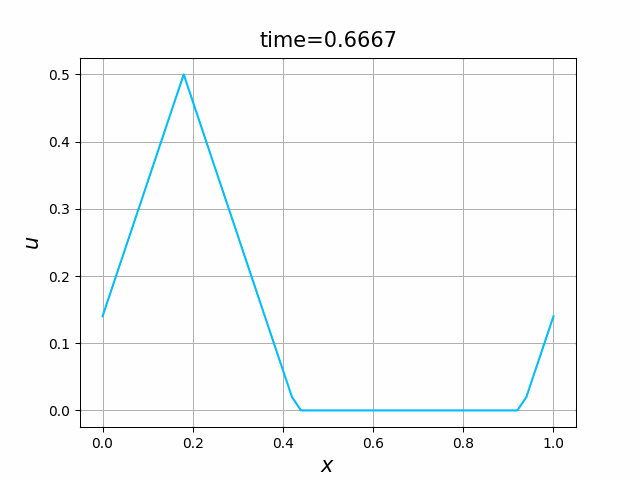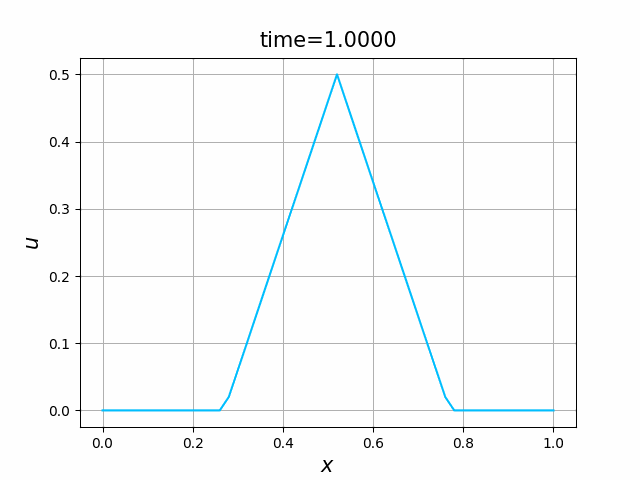
これらを次の In [10] のように実行する．風上差分スキーム(C.7)について，図C.3が$a_1$，図C.4が$a_2$を用いた計算結果である． LF差分スキーム(C.8)について，図C.5が$a_1$，図C.6が$a_2$を用いた計算結果である．

In [10]:
# 初期値
def initial1(x):
  return np.sin(4*np.pi*x)

def initial2(x):
  return np.maximum(0.0, np.minimum(2.0*x-0.5, 1.5-2.0*x))

#パラメータの設定
c = 1.0
N = 51
T = 1.0
lam = 1
num = 40

#線形移流方程式の計算
x, tn, sol = linear_advection_upwind(c, initial2, N, T, lam, num)
#x, tn, sol = linear_advection_lax(c, initial1, N, T, lam, num)

#図の表示
plot_solution(x, sol)

#アニメーションを表示
anim = plot_animation(x, tn, sol)
#結果をadvection.gifに保存（Googleドライブをマウントしておくこと！）
anim.save('/content/drive/MyDrive/Colab Notebooks/fig/advection.gif', writer='pillow')
rc('animation', html='jshtml')
plt.close()
anim

変数係数線形移流方程式に対する差分スキーム

変数係数の線形移流方程式を考えよう： \begin{align} u_t+f(x,t)u_x&=g(x,t),&& x\in \mathbb{T},~t\in (0,T),\tag{C.9a}\\ u(x,0)&=a(x),&& x\in \mathbb{T}.\tag{C.9b} \end{align} ここで， $f:\mathbb{R}\times [0,T]\to\mathbb{R}$， $g:\mathbb{R}\times [0,T]\to\mathbb{R}$， ${a}:\mathbb{R}\to\mathbb{R}$，は与えられた関数である．

\begin{equation} f_i^n=f(x_i,t_n),\quad g_i^n=g(x_i,t_n) \end{equation} とおく．さらに， \begin{equation} [s]_+=\max\{s,0\},\quad [s]_-=\max\{-s,0\},\quad s=[s]_+-[s]_{-} \end{equation} と記号を定め， \begin{equation} f_i^{n,+}=[f_i^n]_+,\quad f_i^{n,-}=[f_i^n]_-,\quad f_i^n=f_i^{n,+}-f_i^{n,-} \end{equation} と書く．

(C.9)に対する風上スキームは， \begin{equation*} \frac{u^{n+1}_i-u_i^n}{\tau}+ f_i^{n,+}\frac{u_{i}^n-u_{i-1}^n}{h}- f_i^{n,-}\frac{u_{i+1}^n-u_{i}^n}{h}=g_i^n \end{equation*} となる．すなわち， \begin{equation} \tag{C.10} u^{n+1}_i = u_i^n-f_i^{n,+}\frac{\tau}{h}(u_{i}^n-u_{i-1}^n)+ f_i^{n,-}\frac{\tau}{h}(u_{i+1}^n-u_{i}^n)+\tau g_i^n \end{equation} となる．初期条件は，(C.4)と同じである．これを実行するために， In [11] を用意する．

(C.9)に対するLFスキームは， \begin{equation*} \frac{u^{n+1}_i-\frac{u^n_{i-1}+u^n_{i+1}}{2}}{\tau} +f_i^{n}\frac{u_{i+1}^n-u_{i-1}^n}{2h}=g_i^n \end{equation*} すなわち， \begin{equation} u_i^{n+1} =\frac{u_{i-1}^n+u_{i+1}^n}{2}- f_i^{n}\frac{\tau}{2h}(u_{i+1}^n-u_{i-1}^n)+\tau g_i^n \tag{C.11} \end{equation} となる．初期条件は，(C.4)と同じである．これを実行するために， In [12] を用意する．

In [11]: 
#変数係数線形移流方程式に対する風上差分スキーム
def variable_advection_upwind(func_f, fmax, func_g, initial, N, T, lam, num):
  L = 1.0
  h = L/N
  tau = lam*h/fmax
  nmax = int(T/tau)
  step = int(max(1, nmax/num))
  mu = tau/h
  theta = 1 if c >= 0 else 0

  xgrid = np.linspace(0.0, L, N)
  xtmp = np.copy(xgrid[0:N-1])
  tgrid = np.array([0.0])
  u = initial(xtmp)
  sol = np.copy(np.append(u,u[0]))

  tnow = 0.0
  for n in range(nmax):
    coef_f = func_f(xtmp, tnow)
    coef_fp = np.maximum(coef_f, 0.0)
    coef_fm = np.maximum(-coef_f, 0.0)
    coef_g = func_g(xtmp, tnow)
    u = u - mu*coef_fp*(u - np.roll(u,1)) + mu*coef_fm*(np.roll(u,-1) - u) + tau*coef_g
    tnow = (n+1)*tau
    if (n+1)%step==0:
      sol=np.vstack((sol,np.append(u,u[0])))
      tgrid=np.append(tgrid, tnow)

  return xgrid, tgrid, sol

In [12]:  
#変数係数線形移流方程式に対するLF差分スキーム
def variable_advection_lax(func_f, fmax, func_g, initial, N, T, lam, num):
  L = 1.0
  h = L/N
  tau = lam*h/fmax
  nmax = int(T/tau)
  step = int(max(1, nmax/num))
  mu = tau/h
  theta = 1 if c >= 0 else 0

  xgrid = np.linspace(0.0, L, N)
  xtmp = np.copy(xgrid[0:N-1])
  tgrid = np.array([0.0])
  u = initial(xtmp)
  sol = np.copy(np.append(u,u[0]))

  tnow = 0.0
  for n in range(nmax):
    coef_f = func_f(xtmp, tnow)
    coef_g = func_g(xtmp, tnow)
    u = 0.5*(np.roll(u,-1) + np.roll(u,1)) - 0.5*mu*coef_f*(np.roll(u,-1) - np.roll(u,1)) + tau*coef_g
    tnow = (n+1)*tau
    if (n+1)%step==0:
      sol=np.vstack((sol,np.append(u,u[0])))
      tgrid=np.append(tgrid, tnow)

  return xgrid, tgrid, sol

初期関数と係数関数を， \begin{align} a(x)&=a_3(x) =\sin(2\pi x),\tag{C.6a}\\ f(x,t)&=f_3(x,t) =1\tag{C.6b}\\ g(x,t)&=g_3(x) =0\tag{C.6c} \end{align} と選ぶ．すると，(C.9)の厳密解は， \begin{equation} u(x,t) =\sin(2\pi (x-t))\tag{C.7} \end{equation} となる．また，初期関数と係数関数を， \begin{align} a(x)&=a_4(x) =\sin(2\pi x),\tag{C.8a}\\ f(x,t)&=f_4(x,t) =\cos(2\pi x)\tag{C.8b}\\ g(x,t)&=g_4(x) =-2\pi \cos(2\pi(x-t))+2\pi\cos(2\pi x)\cos(2\pi(x-t)) \tag{C.8c} \end{align} と選んでも，(C.9)の厳密解は，(C.7)である． In [11] （風上スキーム）を実行してみる．図C.7が，(C.6)を持ちいたとき，図C.8が，(C.8)を持ちいたときの結果である．

In [13]:  
# 初期値
def initial1(x):
  return np.sin(2*np.pi*x)

def func_f1(x, t):
  return np.ones(len(x))
  
def func_g1(x, t):
  return np.zeros(len(x))
  
#パラメータの設定
fmax = 1.0
N = 51
T = 1.0
lam = 1.0
num = 40

#変数係数線形移流方程式の計算
x, tn, sol = variable_advection_upwind(func_f, fmax, func_g, initial1, N, T, lam, num)
#x, tn, sol = variable_advection_lax(func_f1, fmax, func_g1, initial1, N, T, lam, num)

#図の表示
plot_solution(x, sol)

#アニメーションを表示
anim = plot_animation(x, tn, sol)
#結果をadvection.gifに保存（Googleドライブをマウントしておくこと！）
anim.save('/content/drive/MyDrive/Colab Notebooks/fig/advection.gif', writer='pillow')
rc('animation', html='jshtml')
plt.close()
anim

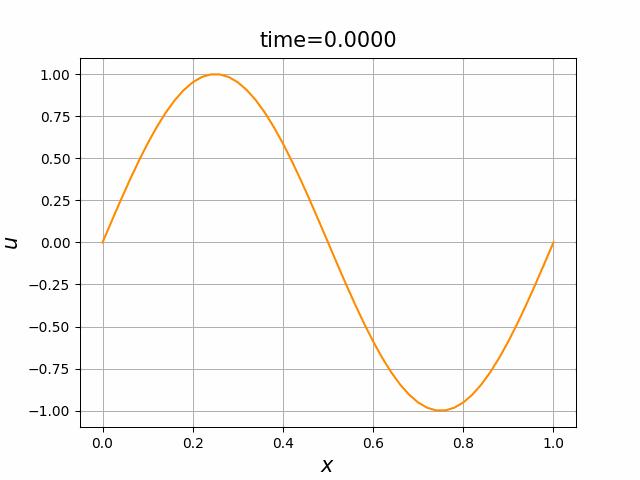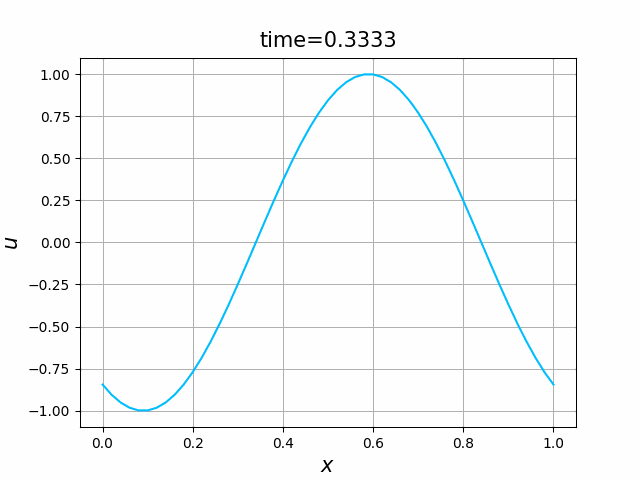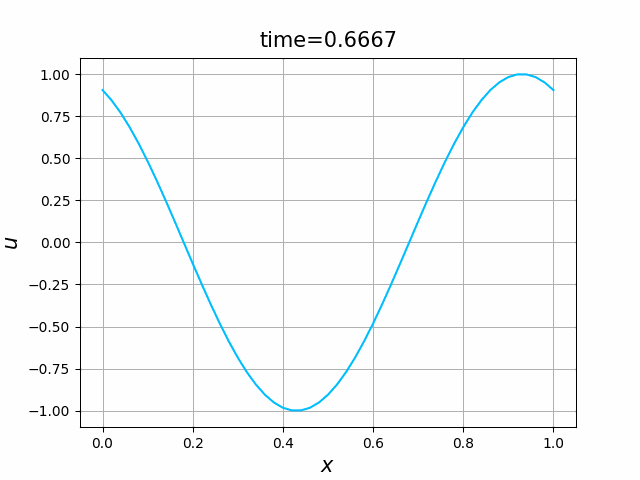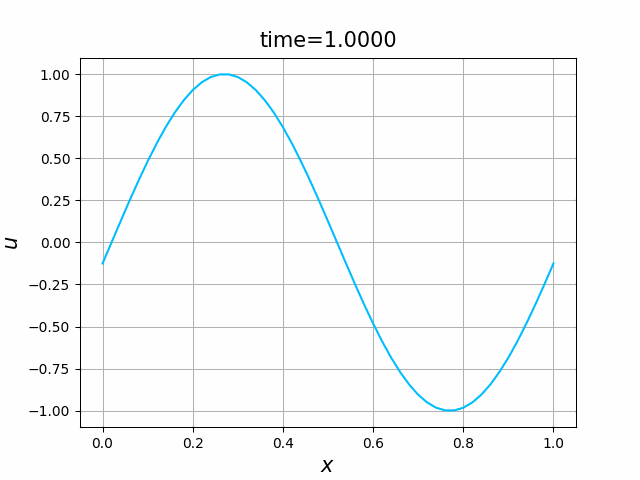
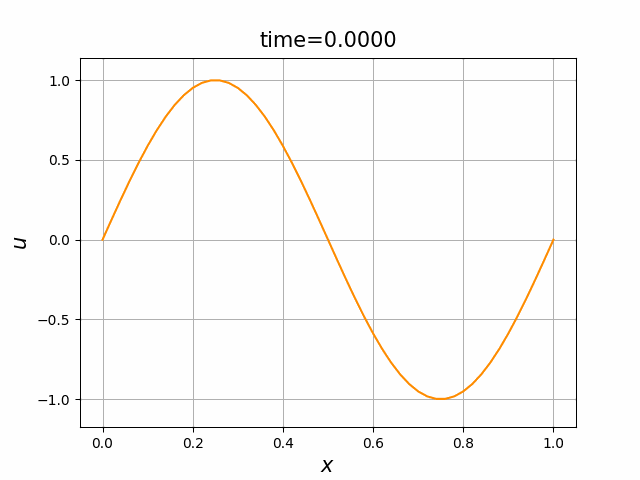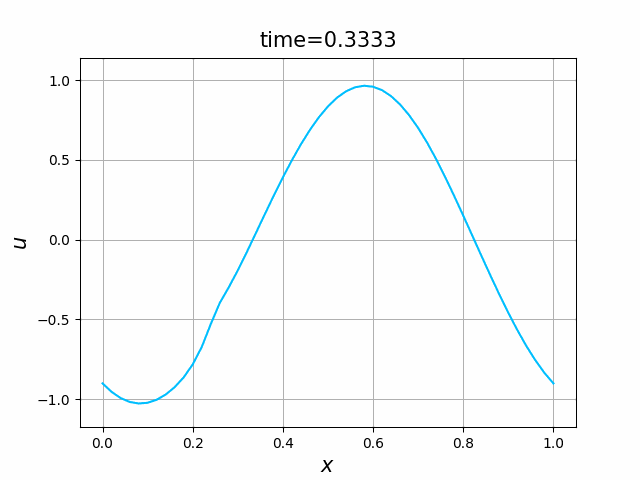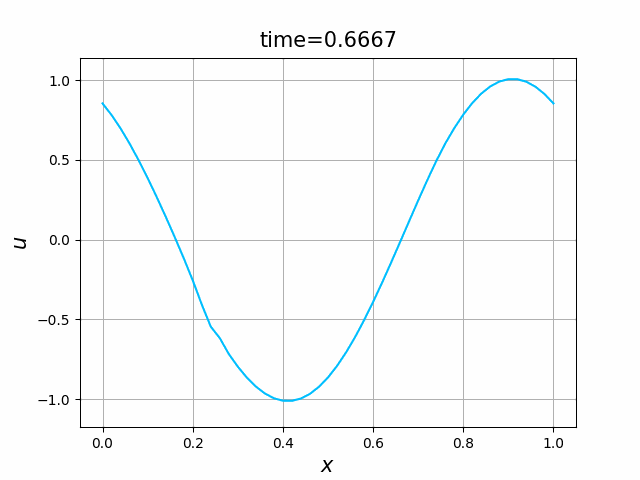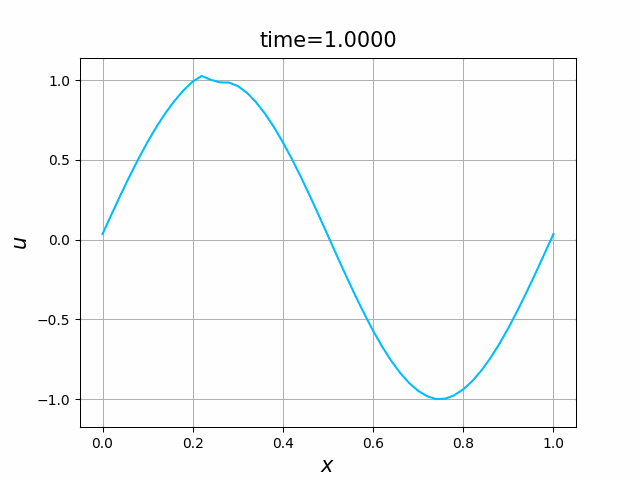
図C.7と図C.8を比べると，厳密解は同じであるが，変数係数の場合の方が，誤差は大きくなっているようである．

そこで，誤差を詳しく調べてみよう．次を講義で示した．

定理． 変数係数の線形移流方程式の初期値問題(C.9)の解 $u$ は，$Q=\mathbb{T}\times [0,T]$ 上で $C^2$ 級とする．このとき，風上スキーム(C.10)の解 $u_i^n$ について，条件 \[ \|f\|_{\infty}\frac{\tau}{h}\le 1 \] の下で， \[ \max_{0\le t_n\le T}\|\boldsymbol{e}^{(n)}\|_\infty\le h \|f\|_\infty\frac{T}{2}\left(\|u_{tt}\|_{\infty}+ \|u_{xx}\|_{\infty}\right) \] が成り立つ．ただし， $\boldsymbol{e}^{(n)}=(e_1^n,\ldots,e_N^n)$， $e_i^n = u_i^n - u(x_i,t_n)$ である．

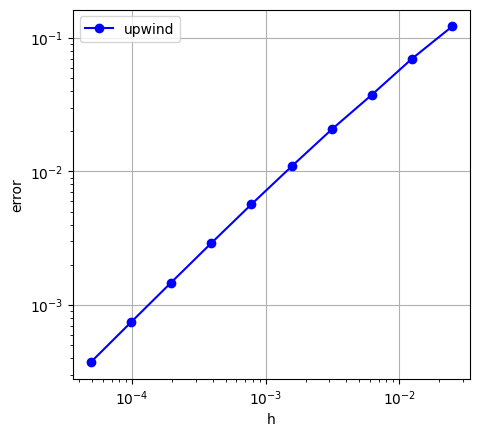
これを計算で確かめるために，In [14]を用意する．説明は，Aですでに述べた通りである．風上差分スキームに対して，In [15]のように実行する．Out [15]を見ると，分割が荒いときには十分な精度は出ていないが，分割を細かくすると，期待する $O(h)$ に近づくことがわかる．

In [14]:  
#誤差の計算、変数係数線形移流方程式
def error_advection(L, func_f, fmax, func_g, initial, exact_sol, lam):
  T = 1.0
  lam = 1.0
  N = 20
  num = 40

  kmax = 10
  hv = np.zeros(kmax)
  ev = np.zeros(kmax)

  for k in range(kmax): 
    N = N*2
    x, tn, sol = variable_advection_upwind(func_f, fmax, func_g, initial, N, T, lam, num)
    #x, tn, sol = variable_advection_lax(func_f, fmax, func_g, initial, N, T, lam, num)
    err = 0.0
    for n in range(tn.shape[0]):
      tval = tn[n]
      err = np.maximum(err, np.linalg.norm(sol[n,:] - exact_sol(x, tval), ord=np.inf))
    hv[k] = L/N
    ev[k] = err

  rate=(np.log(ev[1:]) - np.log(ev[:-1])) / (np.log(hv[1:]) - np.log(hv[:-1]))
  
  return hv, ev, rate

In [15]:
# 初期値
def initial4(x):
  return np.sin(2*np.pi*x)

def func_f4(x, t):
  return np.cos(2.0*np.pi*x)

def func_g4(x, t):
  return -2.0*np.pi*np.cos(2.0*np.pi*(x - t)) + np.cos(2.0*np.pi*x)*2.0*np.pi*np.cos(2.0*np.pi*(x-t))
  
def solution(x, t):
  return np.sin(2.0*np.pi*(x - t))

#パラメータの設定
L = 1.0
T = 1.0
lam = 1.0
fmax = 1.0

#変数係数移流方程式の計算
hv, ev, rate = error_advection(L, func_f4, fmax, func_g4, initial4, solution, lam)

#収束の速さの出力
for i in range(rate.shape[0]-1):
  print(f'{hv[i+1]:.3f}, {rate[i]:.3f}')

#結果の描画（両対数目盛）
plt.plot(hv, ev, 'bo-')   
plt.xscale('log')
plt.yscale('log')
plt.legend(['explicit'])  
plt.xlabel('h')
plt.ylabel('error')
plt.grid('on')
plt.gca().set_aspect('equal', adjustable='box') 
plt.show()  

Out [15]: 
0.013, 0.803
0.006, 0.898
0.003, 0.864
0.002, 0.922
0.001, 0.943
0.000, 0.968
0.000, 0.981
0.000, 0.989

Hamilton--Jacobi方程式に対する差分スキーム

次の形のHamilton--Jacobi方程式を $\mathbb{T}=\mathbb{R}/\mathbb{Z}$ 上で考える： \begin{align} u_t+H(u_x)&=g(x,t),&& x\in\mathbb{T},\ t\in (0,T),\tag{C.9a} \\ u(x,0)&=a(x),&& x\in\mathbb{T}.\tag{C.9b} \end{align} ただし， $g:\mathbb{T}\times [0,T]\to \mathbb{R}$, $a:\mathbb{T}\to \mathbb{R}$ は与えられた関数である．講義では，$g\equiv 0$の場合のみを説明したので注意せよ!

ハミルトニアン $H:\mathbb{R}\to \mathbb{R}$ について以下を仮定する： \begin{gather} \mbox{凸性: }\ H((1-\theta)p+\theta q)\le (1-\theta)H(p)+\theta H(q)\quad (\forall p,q\in \mathbb{R},~\forall \theta\in [0,1]),\label{eq:HJ1c}\\ \mbox{単調性: }\ \begin{cases} H'(p)\le 0 & (p\le p_0),\\ H'(p)\ge 0 & (p\ge p_0). \end{cases} \label{eq:HJ1d} \end{gather}

次のように記号を定める． \begin{equation*} \delta^{+}_h u_i^n=\frac{u^n_{i+1}-u_i^n}{h},\quad \delta^-_h u_i^n=\frac{u^n_{i}-u_{i-1}^n}{h}. \label{eq:fdq1} \end{equation*} (C.9)に対するLF差分スキームは， \begin{equation} u_i^{n+1}=\frac{u_{i-1}^n+u_{i+1}^n}{2}-\tau H\left(\frac{\delta^-_h u_i^n+\delta^+_h u_i^n}{2}\right)+\tau g_i^n \tag{C.10} \end{equation} である．さらに，風上差分スキームは， \begin{equation} u_i^{n+1}=u_i^n-\tau \left[ \theta(\delta^+_h u_i^n)(H(\delta^+_h u_i^n)-H(p_0)) \right. \\ \left. +(1-\theta(\delta^-_h u_i^n))(H(\delta^-_h u_i^n)-H(p_0)) +H(p_0)\right]+\tau g_i^n \tag{C.11} \end{equation} である．ただし， \[ \theta (p)= \begin{cases} 1 & (s\le p_0)\\ 0 & (s> p_0) \end{cases} \] としている．これらは，[CL1984]による（[FF2014]も参考になる）．

講義では次を説明した（[CL1984]のTheorem 1，[FF2014]の§5.2.1--5.2.2）． $b>0$を固定して， \begin{equation} M(b)=\max_{|p|\le b}|H'(p)|\qquad \left(H'(p)=\frac{dH(p)}{dp}\right) \end{equation} とおく．

定理. 初期値は，有界でLipschitz連続とする： \begin{equation*} |a(x)-a(x')|\le L|x-x'|\qquad (x,x'\in\mathbb{T}). \end{equation*} HJ方程式の初期値問題(C.9)の粘性解を $u=u(x,t)$ とする．まず，条件 \begin{equation} M(L+1)\frac{\tau}{h}\le 1 \tag{C.12a} \end{equation} の下で，LFスキーム(C.10)の解 $u_i^n$ は， \begin{equation*} \max_{\begin{subarray}{c} 0\le i\le N-1\\ 0\le n\le M \end{subarray}} |u(x_i,t_n)-u_i^n|\le C\tau^{1/2} \end{equation*} を満たす．ただし，$C$ は，$a$，$L$，$T$ のみ依存して定まる正定数である．さらに，条件 \begin{equation} 2M(L+1)\frac{\tau}{h}\le 1 \tag{C.12b} \end{equation} の下で，風上スキーム (C.11)の解 $u_i^n$ も，同様の誤差評価式を満たす．

LF差分スキームを実行するために，In [16]を用意する．この関数では，(C.12a)を満たすために，$\textup{ML}=M(L+1)$ と$\lambda\le 1$ の値を指定して，$\tau=\lambda h/\textup{ML}$ で，$\tau$ の値を定めている．

In [16]:  
def hj_lax(Hamil, func_g, ML, initial, N, T, lam, num):
  L = 1.0 #これは区間の長さであり，Lipschitz係数ではない
  h = L/N
  tau = lam*h/ML
  nmax = int(T/tau)
  step = int(max(1, nmax/num))

  xgrid = np.linspace(0.0, L, N)
  xtmp = np.copy(xgrid[0:N-1])
  tgrid = np.array([0.0])
  u = initial(xtmp)
  sol = np.copy(np.append(u,u[0]))

  tnow = 0.0
  for n in range(nmax):
    coef_g = func_g(xtmp, tnow)
    u = 0.5*(np.roll(u,1) + np.roll(u,-1)) - tau*Hamil(0.5*(np.roll(u,-1)-np.roll(u,1))/h) + tau*coef_g
    tnow = (n+1)*tau
    if (n+1)%step==0:
      sol=np.vstack((sol,np.append(u,u[0])))
      tgrid=np.append(tgrid, tnow)

  return xgrid, tgrid, sol

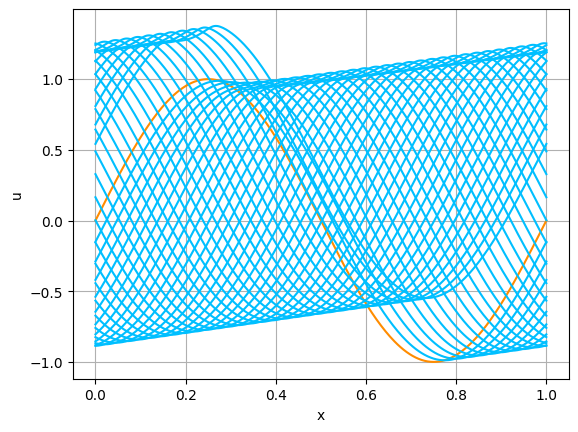
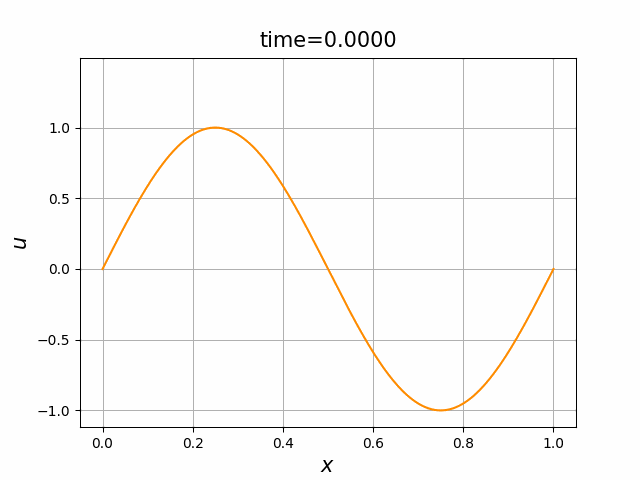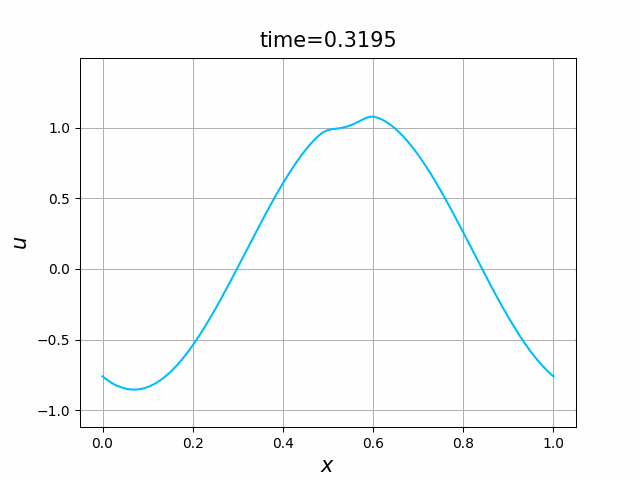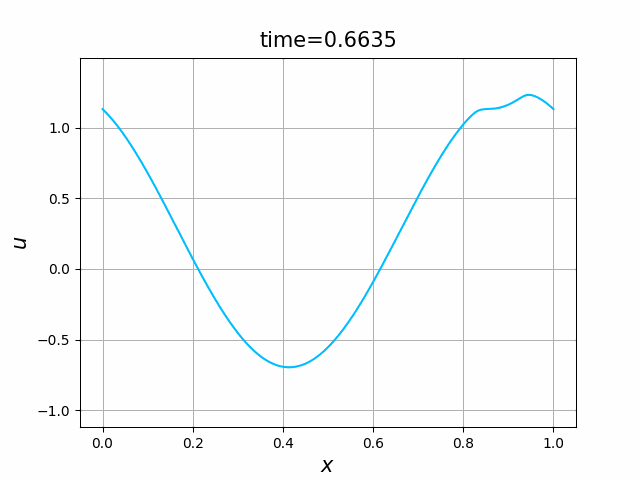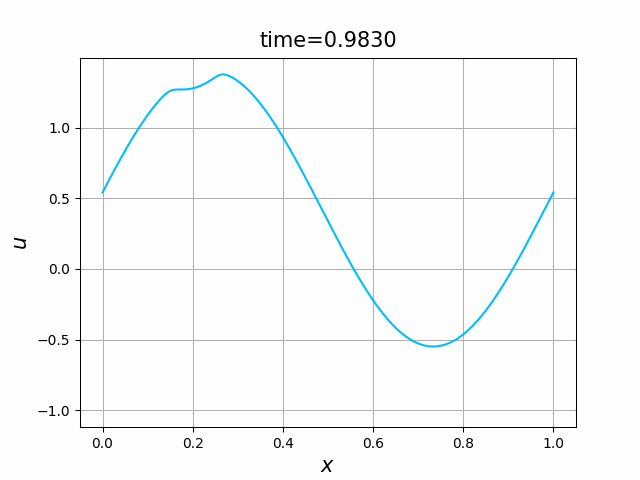
ハミルトニアン，初期関数と係数関数を， \begin{align} H(p)&=H_5(p)=\frac12 p^2,\tag{C.13a}\\ a(x)&=a_5(x) =\sin(2\pi x),\tag{C.13b}\\ g(x,t)&=g_5(x) =-2\pi \cos(2\pi(x-t))+2\pi^2\cos^2(2\pi(x-t)) \tag{C.13c} \end{align} と選ぶ．すると，(C.9)の厳密解は， \begin{equation} u(x,t) =\sin(2\pi (x-t))\tag{C.7} \end{equation} となる．また，$L=2\pi$ ととれるので，$M(L+1)=M(2\pi+1)=2\pi+1$ となる．これらに対して， In [17] のようにLF差分スキームを実行してみる．結果を，図C.10に示す．$N=301$としているが，近似の精度はあまり良くないようである．誤差の挙動を調べることで，収束自体はしていることが確かめられる．すなわち，近似の精度はあまり良くないのは，$h$ や $\tau$ が十分には小さくとれていないことが原因であることがわかる．

In [17]:  
# Hamiltonian
def Hamil(x):
  return 0.5*x*x

# 初期値
def initial(x):
  return np.sin(2.0*np.pi*x)

#右辺関数
def func_g(x, t):
  y = np.pi*np.cos(2.0*np.pi*(x - t))
  return 2.0*y*(y - 1.0)

#パラメータの設定
N = 301
T = 1.0
lam = 1.0
num = 40
#
p0 = 0.0
ML = 7.3

#HJ方程式の計算
x, tn, sol = hj_lax(Hamil, func_g, ML, initial, N, T, lam, num)

#図の表示
plot_solution(x, sol)

#アニメーションを表示
anim = plot_animation(x, tn, sol)
#結果をheat.gifに保存（Googleドライブをマウントしておくこと！）
anim.save('/content/drive/MyDrive/Colab Notebooks/fig/hj.gif', writer='pillow')
rc('animation', html='jshtml')
plt.close()
anim

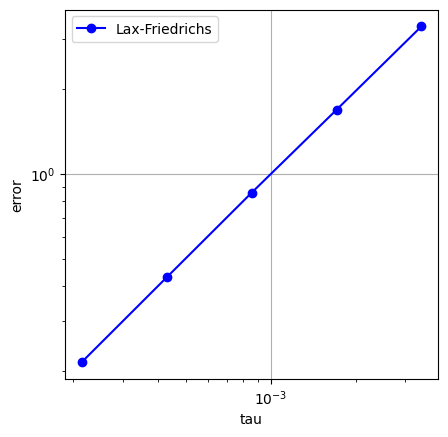
線形移流方程式の場合と同様に誤差を観察しよう．そのために， In [18]と In [19]を用意する．ただし，今度は，$\tau$ に対する誤差を計算するように修正した． (C.13)に対して実行すると，結果は，Out [19]のようになる．この結果からは，誤差は $\tau$ に比例して $0$ に減衰するようである．上の定理から予想される減衰の速さよりも，だいぶ速い．定理は微分可能性を持たないような解に対しても成立する一般的なものであり，一方で，今計算しているのは，非常に滑らかな解である．したがって，定理の主張よりも速く収束しても不思議はない．そもそも，不等式なので矛盾はしていない．

In [18]:  
#誤差の計算、HJ方程式
def error_hj(L, Hamil, ML, func_g, initial, exact_sol, lam):
  T = 1.0
  N = 20
  num = 40

  kmax = 5
  tauv = np.zeros(kmax)
  ev = np.zeros(kmax)

  for k in range(kmax):
    N = N*2
    x, tn, sol = hj_lax(Hamil, func_g, ML, initial, N, T, lam, num)
    err = 0.0
    for n in range(tn.shape[0]):
      tval = tn[n]
      err = np.maximum(err, np.linalg.norm(sol[n,:] - exact_sol(x, tval), ord=np.inf))
    h = L/N
    tauv[k] = lam*h/ML
    ev[k] = err


  rate=(np.log(ev[1:]) - np.log(ev[:-1])) / (np.log(tauv[1:]) - np.log(tauv[:-1]))  

  return tauv, ev, rate

In [19]: 
# Hamiltonian
def Hamil(p):
  return 0.5*p*p

# 初期値
def initial(x):
  return np.sin(2.0*np.pi*x)

#右辺関数
def func_g(x, t):
  y = np.pi*np.cos(2.0*np.pi*(x - t))
  return 2.0*y*(y - 1.0)

def solution(x, t):
    return np.sin(2.0*np.pi*(x-t))

#パラメータの設定
L = 1.0  #これは区間の長さであり，Lipschitz係数ではない
T = 1.0
lam = 1.0
ML = 7.3

#HJ方程式の計算
tauv, ev, rate = error_hj(L, Hamil, ML, func_g, initial, solution, lam)

#収束の速さの出力
for i in range(rate.shape[0]-1):
  print(f'{tauv[i+1]:.3f}, {rate[i]:.3f}')

#結果の描画（両対数目盛）
plt.plot(tauv, ev, 'bo-')
plt.xscale('log')
plt.yscale('log')
#plt.legend(['upwind'])
plt.legend(['Lax-Friedrichs'])
plt.xlabel('tau')
plt.ylabel('error')
plt.grid('on')
plt.gca().set_aspect('equal', adjustable='box')
plt.show()

Out [19]: 
0.002, 0.982
0.001, 0.977
0.000, 0.996

問題

上記の入力と出力をすべて確かめよ．
パラメータ値を変えて，計算を再試行せよ．
例題を自分で設定して，上記の方法を試せ．

課題

課題C.1

自分で例題を設定して，変数係数線形移流方程式に対するLax--Friedrichs差分スキームの誤差の減衰の速さについて調べよ．すなわち，風上差分スキームに対するOut [15]に相当する計算を行え．

課題C.2

例題を自分で設定して，Hamilton--Jacobi方程式に対して，風上差分スキームを実行せよ．（計算結果を示すのみで良い．）

参考文献

[CL1984] M. G. Crandall and P. L. Lions, Two approximations of solutions of Hamilton--Jacobi equations, Math. Comp. 43, No. 167 (1984) 1--19.
[FF2014] M. Falcone and R. Ferretti, Semi-Lagrangian Approximation Schemes for Linear and Hamilton--Jacobi Equations, Society for Industrial and Applied Mathematics (SIAM), 2014.