2024-3A 数理情報学（東京大学教養学部） [齊藤宣一] [top] [A] [B] [C] [UTOL]

B. 熱方程式に対する陰的スキーム．半線形反応拡散方程式

熱方程式の陽的スキームの再考察

熱方程式に対する「陰的」差分スキームの計算の準備として， 前節で考察した，熱方程式の初期値境界値問題を，改めて考察する： \begin{align} & \frac{\partial u}{\partial t}=\kappa \frac{\partial^2 u}{\partial x^2} && (0 < x < L,~ t > 0)\tag{A.1a} ,\\ & u(0,t)=0,\quad u(L,t)=0 && (t > 0),\tag{A.1b}\\ & u(x,0)=a && (0\le x\le L). \tag{A.1c} \end{align}

$N$ を正の整数として，$\displaystyle{h=\frac{L}{N+1}}$とおき，$x_i=ih$ $(i=0,1,\ldots,N+1)$ と定める．次に，正の定数$\tau$ を固定して，$t_n=n\tau$ $(n=0,1,\ldots)$とおく．この格子点の各点 $(x_i,t_n)$ で，初期値境界値問題の解 $u(x_i,t_n)$ の近似値 $u_i^n$ を求めていた．実際，陽的スキームとは，次のものであった： \begin{align} &\frac{u_i^{n+1}-u_i^n}{\tau}=\kappa \frac{u_{i-1}^{n}-2u_i^{n}+u_{i+1}^n}{h^2} && (1\le i\le N,\ n\ge 0) \tag{A.6a},\\ & u_0^n=u_{N+1}^n=0 && (n\ge 1), \tag{A.6b}\\ & u_i^0=a(x_i) && (0\le i\le N+1)\tag{A.6c}. \end{align}

ここで，$\boldsymbol{u}^{(n)}=(u_1^n,\ldots,u_N^n)\in\mathbb{R}^N$， $\boldsymbol{a}=(a(x_1),\ldots,a(x_N))\in\mathbb{R}^N$ とおく．そして，三重対角行列 \begin{equation} \tag{B.1} A=\begin{pmatrix} 2 &-1 &0 &\cdots &0\\ -1 &2 &-1 &\cdots &\\ & &\ddots &\ddots &\\ & \cdots&-1 &2 &-1\\ 0 &\cdots & 0 &-1 &2 \end{pmatrix} \in\mathbb{R}^{N\times N} \end{equation} を導入する．すると，(A.6a,b)は， \[ \frac{1}{\tau} [\boldsymbol{u}^{(n+1)}-\boldsymbol{u}^{(n)}] =-\frac{1}{h^2}A\boldsymbol{u}^{(n)} \] と書ける．したがって，さらに，単位行列 $I\in \mathbb{R}^{N\times N}$ を導入することで，(A.6a,b,c)は， \begin{equation} \tag{B.2} \boldsymbol{u}^{(n)}= \underbrace{(I-\lambda A)}_{=K_\lambda}\boldsymbol{u}^{(n-1)}\quad (n\ge 1),\qquad \boldsymbol{u}^{(0)}=\boldsymbol{a} \end{equation} と書けるのである（後の表記と合わせるために，漸化式も $n$ と $n-1$ の関係に直した）． ここで， $\lambda$ は， \begin{equation} \tag{A.7} \lambda\stackrel{\textrm{def.}}{=} \kappa \frac{\tau}{h^2} \end{equation} で定めたものである． 

In [1]:  
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import animation, rc
from IPython.display import HTML

可視化のためのプログラムは，前回と同じものを使う．

In [2]:  
#図のプロット、一枚の図に、グラフを重ねる
def plot_solution(xgrid, uvect):
  # 描画に関するパラメータの設定
  umax = np.max(sol)
  umin = np.min(sol)
  ulength = umax - umin
  umax += 0.05 * ulength
  umin -= 0.05 * ulength
  # t = 0                  
  plt.plot(xgrid,uvect[0,:],color='#ff8c00')
  # t > 0
  for n in range(1,uvect.shape[0]):
    plt.plot(xgrid,uvect[n,:],color='#00bfff')
  
  plt.xlabel('x')
  plt.ylabel('u')
  plt.ylim(umin, umax)
  plt.grid('on')
  plt.show()

In [3]:  
#アニメーションの作成
# IPython.displayモジュールを使う
def plot_animation(xgrid, tgrid, uvect):
  # 描画に関するパラメータの設定
  umax = np.max(sol)
  umin = np.min(sol)
  xmax = np.max(xgrid)
  xmin = np.min(xgrid)
  ulength = umax - umin
  utop = umax + 0.1*ulength
  umax += 0.05*ulength
  umin -= 0.05*ulength
  xmid = (xmax+xmin)/2
  xlength = xmax - xmin
  xmax += 0.05*xlength
  xmin -= 0.05*xlength
  
  # fig, axオブジェクトを作成
  fig, ax = plt.subplots()
  ims = []
  
  # t = 0
  n = 0
  im, = ax.plot(xgrid, uvect[n, :], color='#ff8c00')
  title = ax.text(xmid, utop, f'time={tgrid[n]:.4f}', ha='center', va='center', fontsize=15)
  ims.append([im, title])
    
  # t > 0
  for n in range(1, uvect.shape[0]):
    im, = ax.plot(xgrid, uvect[n, :], color='#00bfff')
    title = ax.text(xmid, utop, f'time={tgrid[n]:.4f}', ha='center', va='center', fontsize=15)
    ims.append([im, title])
    
  # 各軸のラベル
  ax.set_xlabel(r"$x$", fontsize=15)
  ax.set_ylabel(r"$u$", fontsize=15)
  # グラフの範囲を設定
  ax.set_xlim([xmin, xmax])
  ax.set_ylim([umin, umax])
  ax.grid(True)

  # ArtistAnimationにfigオブジェクトとimsを代入してアニメーションを作成
  return animation.ArtistAnimation(fig, ims)

(B.2)を実行するために，次のようなIn [4] を用意する． In [4] では， $\mathrm{xgrid}=(x_0,x_1,\ldots,x_{N+1})\in\mathbb{R}^{N+2}$ に対して， $\mathrm{ugrid}=(u_0^n,u_1^n,\ldots,u_{N+1}^n)\in\mathbb{R}^{N+2}$ を定めて，さらに， \[ \mathrm{u}= \mathrm{ugrid}[1\mbox{:}N+1]=(u_1^n,u_2^n,\ldots,u_{N}^n)\in\mathbb{R}^{N} \] としている．計算のためには， $\mathrm{u}$ があれば十分だが，可視化のためには， $\mathrm{ugrid}$ が必要となる．また，三重対角行列 $A$ の作り方は，第1節で説明した． 

In [4]:  
#（斉次）熱方程式、零Dirichlet境界条件、陽的スキーム（行列・ベクトル形式）
def heat_0dbc_ex2(L, kappa, initial, N, T, lam, num):
    
  bdy=0.0

  h = L/(N+1)
  tau = lam*h*h/kappa
  nmax = int(T/tau)
  step=int(max(1, nmax/num))
  
  A = 2.0*np.diag(np.ones(N)) - np.diag(np.ones(N-1), 1) - np.diag(np.ones(N-1), -1)
  K = np.eye(N, N) - lam * A

  xgrid = np.linspace(0, L, N+2) 
  tgrid = np.array([0.0])
  ugrid = np.vectorize(initial)(xgrid)
  u = np.copy(ugrid[1:N+1])
  sol = np.copy(ugrid)
  
  for n in range(nmax):
    tnow = (n+1)*tau
    u = np.dot(K,u)
    if (n+1)%step==0.0:
      ugrid = np.append(bdy, np.append(u, bdy))
      sol = np.vstack((sol,ugrid))
      tgrid = np.append(tgrid, tnow)
    
  return xgrid, tgrid, sol

これを次のように実行する．同じことをしているのだから，前回の図A.3と結果は同じになる．

In [5]:  
# 初期値
def initial1(x):
  return min(x,1-x)
  
#パラメータの設定
L = 1.0
kappa = 1.0
N = 51
T = 1.0
lam = 0.4
num = 60

#熱方程式の計算
x, tn, sol = heat_0dbc_ex2(L, kappa, initial1, N, T, lam, num)

#図の表示
plot_solution(x, sol)
図2.1
図B.1 Out [5]

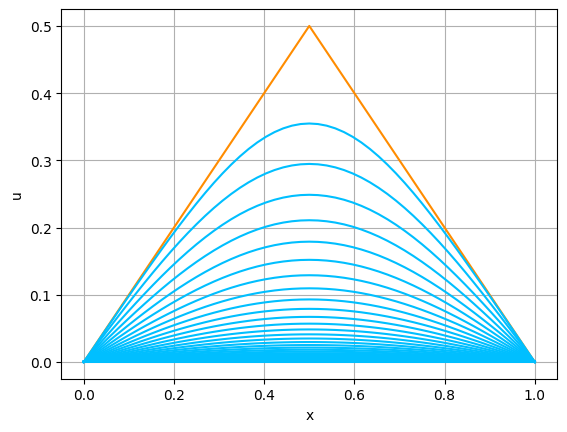
さて，ここで，改めて，行列 $A$，あるいは，$K_\lambda$ の形をよく見てみると，これらの成分はほとんどが $0$ である．したがって，$A\boldsymbol{u}^{(n-1)}$ の計算の際に， $0\times \mbox{(なんとか)}$ という自明な計算が，全体の計算量の大部分を占めており，効率が悪い．このように，成分のほとんどが零であるような行列を，疎行列 (sparse matrix)と言う．ただし，「成分のほとんど」に対して明確な定義は存在しない． 非零成分が，行数（あるいは列数）の定数（$\le 10$ 程度）倍であれば，疎行列と言って良いと思う．

scipyモジュールをインポートすることで，疎行列を簡単に扱うことができる．

In [6]:  
from scipy.sparse import csc_matrix, csr_matrix

疎行列を格納するフォーマットは数種類ある．圧縮列格納方式 (compressed sparse column, CSC / compressed column storage, CCS) 方式と圧縮行格納方式 (compressed sparse row, CSR / compressed row storage, CRS)方式が有名である．詳しい定義などは，例えば， [Barrett]を参照せよ（あるいは，検索すればいくらでも情報が得られる）． ここでは，例のみで説明する． 

In [7]:  
N=6
A = 2.0*np.diag(np.ones(N)) - np.diag(np.ones(N-1), 1) - np.diag(np.ones(N-1), -1)
Ac = csc_matrix(A)
Ar = csr_matrix(A)
print(type(A))
print(A)
print(type(Ac))
print(Ac)
print(type(Ar))
print(Ar)
  
Out [7]: 
<  class 'numpy.ndarray' > 
[[ 2. -1.  0.  0.  0.  0.]
 [-1.  2. -1.  0.  0.  0.]
 [ 0. -1.  2. -1.  0.  0.]
 [ 0.  0. -1.  2. -1.  0.]
 [ 0.  0.  0. -1.  2. -1.]
 [ 0.  0.  0.  0. -1.  2.]]
<  class 'scipy.sparse._csc.csc_matrix' > 
  (0, 0)	2.0
  (1, 0)	-1.0
  (0, 1)	-1.0
  (1, 1)	2.0
  (2, 1)	-1.0
  (1, 2)	-1.0
  (2, 2)	2.0
  (3, 2)	-1.0
  (2, 3)	-1.0
  (3, 3)	2.0
  (4, 3)	-1.0
  (3, 4)	-1.0
  (4, 4)	2.0
  (5, 4)	-1.0
  (4, 5)	-1.0
  (5, 5)	2.0
<  class 'scipy.sparse._csr.csr_matrix' > 
  (0, 0)	2.0
  (0, 1)	-1.0
  (1, 0)	-1.0
  (1, 1)	2.0
  (1, 2)	-1.0
  (2, 1)	-1.0
  (2, 2)	2.0
  (2, 3)	-1.0
  (3, 2)	-1.0
  (3, 3)	2.0
  (3, 4)	-1.0
  (4, 3)	-1.0
  (4, 4)	2.0
  (4, 5)	-1.0
  (5, 4)	-1.0
  (5, 5)	2.0

上のIn [7]では，$\mathrm{A}$ をCSC形式で $\mathrm{Ac}$ とし， $\mathrm{A}$ をCSR形式で $\mathrm{Ar}$ としている． CSC形式，CSR形式では，行列の非零成分のみを記憶する．これらの形式の違い，上の例を見れば一目瞭然であろう．

疎行列 $\mathrm{A}$ と，ベクトル $\mathrm{u}$ の積は， $\mathrm{A}\mbox{.dot}(\mathrm{u})$ で計算できる．疎行列を用いて， In [4] を修正してみよう． 

In [8]:  
#（斉次）熱方程式、零Dirichlet境界条件、陽的スキーム（行列・ベクトル形式、CSC）
def heat_0dbc_ex3(L, kappa, initial, N, T, lam, num):

  bdy=0.0

  h = L/(N+1)
  tau = lam*h*h/kappa
  nmax = int(T/tau)
  step=int(max(1, nmax/num))

  A = 2.0*np.diag(np.ones(N)) - np.diag(np.ones(N-1), 1) - np.diag(np.ones(N-1), -1)
  K = csc_matrix(np.eye(N, N) - lam * A)  # KをCSC形式で格納

  xgrid = np.linspace(0, L, N+2)
  tgrid = np.array([0.0])
  ugrid = np.vectorize(initial)(xgrid)
  u = np.copy(ugrid[1:N+1])
  sol = np.copy(ugrid)

  for n in range(nmax):
    tnow = (n+1)*tau
    u = K.dot(u)  # 疎行列とベクトルの積
    if (n+1)%step==0.0:
      ugrid = np.append(bdy, np.append(u, bdy))
      sol = np.vstack((sol,ugrid))
      tgrid = np.append(tgrid, tnow)

  return xgrid, tgrid, sol

In [9]:  
# 初期値
def initial1(x):
  return min(x,1-x)
  
#パラメータの設定
L = 1.0
kappa = 1.0
N = 51
T = 1.0
lam = 0.4
num = 60

#熱方程式の計算
x, tn, sol = heat_0dbc_ex3(L, kappa, initial1, N, T, lam, num)

#図の表示
plot_solution(x, sol)

結果自体は，図B.1（Out [5]）と同じだが，ここでは，計算時間の違いに着目したい． そのために，前回の，行列を使わずに，ベクトルのまま更新するプログラムも比較の対象としよう．

In [10]:  
#（斉次）熱方程式、零Dirichlet境界条件、陽的スキーム
def heat_0dbc_ex1(L, kappa, initial, N, T, lam, num):
    
  h = L/(N+1)
  tau = lam*h*h/kappa
  nmax = int(T/tau)
  step=int(max(1, nmax/num))
  
  xgrid=np.linspace(0.0, L, N+2)
  tgrid=np.array([0.0])
  u=np.vectorize(initial)(xgrid)
  sol=np.copy(u)
  
  for n in range(nmax):
    u[1:N+1] = (1-2*lam)*u[1:N+1]+lam*(u[0:N]+u[2:N+2])
    tnow = (n+1)*tau
    if (n+1)%step==0:
      sol=np.vstack((sol,u))
      tgrid=np.append(tgrid, tnow)

  return xgrid, tgrid, sol

In [11]:  
import time

# 初期値
def initial1(x):
  return min(x,1-x)

#パラメータの設定
L = 1.0
kappa = 1.0
N = 100
T = 1.0
lam = 0.4
num = 60

#行列演算
print('vector=')
start = time.perf_counter()
x, tn, sol = heat_0dbc_ex1(L, kappa, initial1, N, T, lam, num)
print(time.perf_counter() - start)

#行列演算
print('matrix=')
start = time.perf_counter()
x, tn, sol = heat_0dbc_ex2(L, kappa, initial1, N, T, lam, num)
print(time.perf_counter() - start)

#疎行列を使った場合
print('sparce matrix=')
start = time.perf_counter()
x, tn, sol = heat_0dbc_ex3(L, kappa, initial1, N, T, lam, num)
print(time.perf_counter() - start)

#図の表示
plot_solution(x, sol)
  
Out [11]: 
vector=
0.37912535199939157
matrix=
0.4581337509998775
sparce matrix=
0.5536915920001775

工夫をするごとに，計算時間がかかっており，あまり苦労の甲斐がない． ただし，In [11]を，$N=500$ として実行した際には，つぎのようになり，疎行列を使った方が，明らかに，効率的である．しかし，陽的スキームを（pythonで）計算する限りにおいては，ことさら，行列演算を持ち込むメリットはなさそうである．しかし，実は，行列表記を用いる動機は，陽的スキームにはなく，次に説明する陰的スキームにある． 

Out [12]: 
vector=
4.702010304000396
matrix=
46.01383844100019
sparce matrix=
6.269569925000724

単純陰的スキーム

熱方程式の初期値境界値問題(A.1a,b,c)の考察に戻ろう．今度は， $\frac{\partial u}{\partial t}(x_i,t_n)$ に後退差分商，$\frac{\partial^2 u}{\partial x^2}(x_i,t_n)$ に2階中心差分商を適用することで，(A.1a)に対する近似方程式として， \begin{equation*} \frac{u_i^{n}-u_i^{n-1}}{\tau}=\kappa \frac{u_{i-1}^{n}-2u_i^{n}+u_{i+1}^n}{h^2}\qquad (1\le i\le N,\ n\ge 1) \end{equation*} が得られる．境界条件と初期条件は，(A.6b,c)をそのまま使う．このとき，上で導入した記法を，そのまま用いると， \begin{equation} \tag{B.3} \underbrace{(I+\lambda A)}_{=H_\lambda}\boldsymbol{u}^{(n)}= \boldsymbol{u}^{(n-1)}\quad (n\ge 1),\qquad \boldsymbol{u}^{(0)}=\boldsymbol{a} \end{equation} が得られる．この場合，$\boldsymbol{u}^{(n-1)}$ から $\boldsymbol{u}^{(n)}$ を求める際に，係数行列が $H_\lambda$ の連立一次方程式を解かなければならない． このように近似解を計算する際に，連立方程式を解かなければならない方法を， 陰的解法， 陰的差分スキーム， 陰的スキームと呼ぶ． 特に， 後に導入するより一般的な陰的スキームの中で最も単純なスキームであることにより， (B.3)を単純陰的スキームと呼ぶ． 前に述べた(A.6)，あるいは，(B.2)は，連立一次方程式を経由しなくても値の更新ができた． したがって，陰的に対して陽的と呼んだのである．

単純陰的スキーム(B.3)について，次のことが知られている（[齊藤2023]，[Saito2018]など）：

陽的スキームの場合は，$\lambda\le 1/2$ という制約があったこととは，対照的である．

連立一次方程式を解くにあたって，LU分解を復習しておこう．一般に，行列 $B$ が正則ならば， \[ PB=LU \] と分解できる．ここで，$P$ は（Gaussの消去法における行交換を記録する）順列行列， $L$ は単位下三角行列， $U$ は上三角行列である．これを，行列 $B$ のLU分解と言う．この分解に基づいて， \begin{equation*} B\boldsymbol{v}=\boldsymbol{b} \quad\Leftrightarrow\quad \begin{cases} L\boldsymbol{c}=P\boldsymbol{b} & \\ U\boldsymbol{v}=\boldsymbol{c}& \end{cases} \quad\Leftrightarrow\quad \boldsymbol{v}=U^{-1}(L^{-1}P\boldsymbol{b}) \end{equation*} と考えることができる．係数行列 $B$ が固定されており，とてもたくさんの $\boldsymbol{b}$ について，連立方程式を解く場合には，はじめにLU分解しておき，$L$ と $U$（と $P$）を使って各方程式を解くのが効率的である（例えば，[齊藤2012]の注意B.5.2と注意B.5.3，[齊藤2017]の6.1節を見よ）．

これは次のように実行される．

In [13]:  
from scipy.linalg import lu_factor, lu_solve

n = 5
A = np.random.rand(n, n)
b = np.ones(n)
b = np.dot(A, b)

# LU分解
lu, piv = lu_factor(A)

# 連立方程式の解の計算
x = lu_solve((lu, piv), b)

print(x)
  
Out [13]: 
[1. 1. 1. 1. 1.]

疎行列を使う場合には，次のようにする．

In [14]:  
from scipy.sparse.linalg import splu

N = 6
A = 2.0*np.diag(np.ones(N)) - np.diag(np.ones(N-1), 1) - np.diag(np.ones(N-1), -1)
H = csc_matrix(np.eye(N, N) + A)
b = 2.0*np.ones(N)
b = H.dot(b)

# LU分解
LU = splu(H)

# LU分解に基づいて連立方程式を解く
x = LU.solve(b)

print(x)
  
Out [14]: 
[2. 2. 2. 2. 2. 2.]

注意. spluに渡す行列は，CSC形式で記述されている必要がある．したがって， CSR形式の行列を渡すと，CSC形式に変換する（これはpythonが勝手にやってくれる）という手間が増えてしまう．そのため，本講義では，CSC形式のみを，主に扱っている．

さて，(B.3)の実行に進む前に，今後必要になる モジュールをまとめて，インポートしておこう．すでにインポートしているものも多いが，確認のためでもある．

In [15]:  
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import animation, rc
from IPython.display import HTML
from scipy.linalg import lu_factor, lu_solve
from scipy.sparse import csc_matrix, csr_matrix
from scipy.sparse.linalg import spsolve, splu

In [16]:  
#（斉次）熱方程式、零Dirichlet境界条件、単純陰的スキーム（行列・ベクトル形式）
def heat_0dbc_implicit1(L, kappa, initial, N, T, lam, num):

  bdy=0.0

  h = L/(N+1)
  tau = lam*h*h/kappa
  nmax = int(T/tau)
  step=int(max(1, nmax/num))

  A = 2.0*np.diag(np.ones(N)) - np.diag(np.ones(N-1), 1) - np.diag(np.ones(N-1), -1)
  H = np.eye(N, N) + lam * A
  lu, piv = lu_factor(H) # LU分解

  xgrid=np.linspace(0, L, N+2)
  tgrid=np.array([0.0])
  ugrid = np.vectorize(initial)(xgrid)
  u = np.copy(ugrid[1:N+1])
  sol=np.copy(ugrid)

  for n in range(nmax):
    tnow = (n+1)*tau
    u = lu_solve((lu, piv), u) # 連立一次方程式の解法
    if (n+1)%step==0.0:
      ugrid = np.append(bdy, np.append(u, bdy))
      sol = np.vstack((sol,ugrid))
      tgrid = np.append(tgrid, tnow)

  return xgrid, tgrid, sol

次に，In [16]と同じ計算を，疎行列を用いて行おう． このとき，

In [17]:  
#（斉次）熱方程式、零Dirichlet境界条件、単純陰的スキーム（行列・ベクトル形式、CSCを使う）
def heat_0dbc_implicit2(L, kappa, initial, N, T, lam, num):

  bdy=0.0

  h = L/(N+1)
  tau = lam*h*h/kappa
  nmax = int(T/tau)
  step=int(max(1, nmax/num))

  A = 2.0*np.diag(np.ones(N)) - np.diag(np.ones(N-1), 1) - np.diag(np.ones(N-1), -1)
  H = csc_matrix(np.eye(N, N) + lam * A)
  LU = splu(H)  # LU分解

  xgrid=np.linspace(0, L, N+2)
  tgrid=np.array([0.0])
  ugrid = np.vectorize(initial)(xgrid)
  u = np.copy(ugrid[1:N+1])
  sol = np.copy(ugrid)

  for n in range(nmax):
    tnow = (n+1)*tau
    u = LU.solve(u) # 連立一次方程式の解法 CSC 版
    if (n+1)%step==0.0:
      ugrid = np.append(bdy, np.append(u, bdy))
      sol = np.vstack((sol,ugrid))
      tgrid = np.append(tgrid, tnow)

  return xgrid, tgrid, sol

これらを実行し，さらに，計算時間を比較しよう．

In [18]:
import time

# 初期値
def initial1(x):
  return min(x,1-x)
  
#パラメータの設定
L = 1.0
kappa = 1.0
N = 101
T = 1.0
lam = 0.4
num = 60

# 標準的
print('standard=')
start = time.perf_counter()
x, tn, sol = heat_0dbc_implicit1(L, kappa, initial1, N, T, lam, num)
print(time.perf_counter() - start)

plot_solution(x, sol)

#　疎行列
print('sparse=')
start = time.perf_counter()
x, tn, sol = heat_0dbc_implicit2(L, kappa, initial1, N, T, lam, num)
print(time.perf_counter() - start)

plot_solution(x, sol)  

Out [18]: 
standard=
0.6640573180011415

sparse=
0.39567478200115147

出てくる図は，図B.1（Out [5]）と同じである．しかし，今度は，疎行列であることを利用して連立一次方程式を解いた方が，効率的であることがわかる．

注意． $H_\lambda$ は，疎行列とはいえ，三重対角という特別な形をしているので，1次元配列のみを用いて，三重対角行列に特化した成分の格納法とLU分解に基づいた連立一次方程式の解法を行う関数（例えば，[菊地・山本]などを見よ）を用意しておけば，わざわざ，scipy.sparseの関数を使う必要はない．しかし，便利なモジュールを，どんどん利用して，できるだけ，楽をしてプログラミングできることは，pythonの強みである．

陰的 $\theta$ スキーム

熱方程式(1.1a)の近似として， 陽的スキームと単純陰的スキームを重み係数 $0 \le \theta \le 1$ で荷重平均した， \begin{equation*} \frac{u_i^{n}-u_i^{n-1}}{\tau} = (1-\theta)\kappa \frac{u_{i-1}^{n-1}-2u_i^{n-1}+u_{i+1}^{n-1}}{h^2}+ \theta \kappa \frac{u_{i-1}^{n}-2u_i^{n}+u_{i+1}^n}{h^2} \end{equation*} を考えることができる．境界条件と初期条件は，(A.6b,c)をそのまま使う．いままで導入した記法を，そのまま用いると，これは， \begin{equation} \tag{B.4} \underbrace{(I+\theta\lambda A)}_{=H_{\theta\lambda}}\boldsymbol{u}^{(n)}= \underbrace{(I-(1-\theta)\lambda A)}_{=K_{(1-\theta)\lambda}}\boldsymbol{u}^{(n-1)}\quad (n\ge 1),\qquad \boldsymbol{u}^{(0)}=\boldsymbol{a} \end{equation} と書ける．これを， 陰的$\theta$解法， 陰的$\theta$スキームと呼ぶ． 特に，$\theta=1/2$ のときを，Crank--Nicolsonスキームと呼ぶ．

(B.4)について，次のことが知られている（[齊藤2023]，[Saito2018]など）：

したがって，例えば収束性を得ようとした場合に， Crank--Nicolsonスキームには，$\lambda\le 1$ という制限がつくことになる． 

In [19]:  
#（斉次）熱方程式、零Dirichlet境界条件、陰的thetaスキーム（行列・ベクトル形式、CSCを使う）
def heat_0dbc_theta1(L, kappa, initial, N, T, lam, theta, num):

  bdy=0.0

  h = L/(N+1)
  tau = lam*h*h/kappa
  nmax = int(T/tau)
  step=int(max(1, nmax/num))

  A = 2.0*np.diag(np.ones(N)) - np.diag(np.ones(N-1), 1) - np.diag(np.ones(N-1), -1)
  H = csc_matrix(np.eye(N, N) + theta * lam * A)
  K = csc_matrix(np.eye(N, N) - (1.0 - theta) * lam * A)
  LU = splu(H)  # LU分解

  xgrid = np.linspace(0, L, N+2)
  tgrid = np.array([0.0])
  ugrid = np.vectorize(initial)(xgrid)
  u = np.copy(ugrid[1:N+1])
  sol = np.copy(ugrid)

  for n in range(nmax):
    tnow = (n+1)*tau
    u = LU.solve(K.dot(u)) # 連立一次方程式の解法 CSC 版
    if (n+1)%step==0.0:
      ugrid = np.append(bdy, np.append(u, bdy))
      sol = np.vstack((sol,ugrid))
      tgrid = np.append(tgrid, tnow)

  return xgrid, tgrid, sol

In [20]:  
# 初期値
def initial1(x):
  return min(x,1-x)
  
#パラメータの設定
L = 1.0
kappa = 1.0
N = 101
T = 1.0
lam = 0.4
num = 60

theta = 0.5
x, tn, sol = heat_0dbc_theta1(L, kappa, initial1, N, T, lam, theta, num)

plot_solution(x, sol)

計算結果は，図B.1（Out [5]）と同じである．

次に，$\lambda=1$ として，$\theta=1$ と $\theta=1/2$ のときの誤差を観察しよう．

In [21]:
#誤差の計算、斉次熱方程式、零Dirichlet境界条件、陰的thetaスキーム
def error_heat_theta(L, kappa, initial, righthand, exact, T, lam, theta):

  N = 10
  num = 200

  kmax = 6
  hv = np.zeros(kmax)
  ev = np.zeros(kmax)

  for k in range(kmax):
    N = N*2
    x, tn, sol = heat_0dbc_theta1(L, kappa, initial, N, T, lam, theta, num)
    err = 0.0
    for n in range(tn.shape[0]):
      tval = tn[n]
      err = max(err, np.linalg.norm(sol[n,:] - exact(x, tval), ord=np.inf))
    hv[k] = L/(N+1)
    ev[k] = err

  rate=(np.log(ev[1:]) - np.log(ev[:-1])) / (np.log(hv[1:]) - np.log(hv[:-1]))

  return hv, ev, rate  

In [22]:  
# 初期値 a
def initial2(x):
  return np.sin(np.pi*x)

# 右辺の関数 f
def righthand2(x, t):
  return 0.0

# 厳密解 u
def exact2(x, t):
  return np.exp(-np.pi**2*t)*np.sin(np.pi*x)


#パラメータの設定
L = 1.0
kappa = 1.0
T = 1.0
lam = 1.0
num = 30

#熱方程式の計算
hv1, ev1, rate1 = error_heat_theta(L, kappa, initial2, righthand2, exact2, T, lam, 1.0)
hv2, ev2, rate2 = error_heat_theta(L, kappa, initial2, righthand2, exact2, T, lam, 0.5)

#収束の速さの出力
for i in range(rate1.shape[0]-1):
  print(f'{hv1[i+1]:.3f}, {rate1[i]:.3f}, {rate2[i]:.3f}')

#結果の描画（両対数目盛）
plt.plot(hv1, ev1, 'bo-')
plt.plot(hv2, ev2, 'ro-')
plt.xscale('log')
plt.yscale('log')
plt.legend(['simple implicit','CN'])
plt.xlabel('h')
plt.ylabel('error')
plt.grid('on')
plt.gca().set_aspect('equal', adjustable='box')
plt.show()
  
Out [22]: 
0.024, 1.986, 1.972
0.012, 1.996, 1.993
0.006, 1.999, 1.998
0.003, 2.000, 1.999
図B.2
図B.2 Out [22]

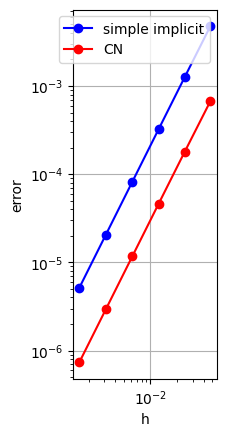
Crank--Nicolsonスキームの場合でも，$\lambda\le 1$ を固定しているので， $O(\tau^2+h^2)=O(h^2)$ となってしまう．したがって，Crank--Nicolsonスキームの， $O(\tau^2+h^2)$ の形の誤差評価は，あまり役に立たないように思える．しかしながら， 実は，Crank--Nicolsonスキームに対しては，$\lambda$ に対する制限なしに， $O(\tau^2+h^2)$ の形の誤差評価が（しかも，$\|\cdot\|_\infty$ に対して）成り立つことが示せる（たとえば，[齊藤2023]）．結果的に， $\lambda$ の値を気にせずに，$h$ と $\tau$ を独立に，十分小さくとっても良いのである．

Neumann境界条件

Neumann境界条件 \begin{equation} \tag{B.5} \frac{\partial u}{\partial x}(0,t)=0,\quad \frac{\partial u}{\partial x}(L,t)=0 \qquad (t>0) \end{equation} の下で，熱方程式(A.1a)を考える．初期条件は，(A.1c)とする．

$h$ を $\displaystyle{h=\frac{L}{N}}$ で定めて， 格子点 $({x}_i=ih,t_n=n\tau)$ $(-1\le i\le N+1, n\ge 0)$ を考える． ${x}_{-1}=-h$ と ${x}_{N+1}=1+h$ は区間 $0\le x\le 1$ の外に配置されている．このような格子点を仮想格子点と呼ぶ．格子点 $({x}_i,t_n)$ 上での解 $u(x,t)$ の近似値を $u_i^n$ で表す．

まず，陽的スキームを考える．方程式(A.1a)を， \begin{equation*} \frac{u_i^{n+1}-u_i^{n}}{\tau}=\kappa \frac{u_{i-1}^n-2u_{i}^n+u_{i+1}^n}{h^2} \qquad (0\le i\le N,\ n\ge 0) \end{equation*} と近似する．しかし，$i=0,N$ とした際に $u_{-1}^n$ と $u_{N+1}^n$ が現れてしまう．これらを，Neumann境界条件を利用して処理する．具体的には，$x=0$ と $x=1$ を中心とした中心差分商を応用して \begin{equation*} \frac{u^{n}_{1}-u^n_{-1}}{2h}=0,\qquad \frac{u^{n}_{N+1}-u^n_{N-1}}{2h}=0 \end{equation*} と考え，$u_{-1}^{n}=u_1^n$，$u_{N+1}^n=u_{N-1}^n$ とする．

結果として，陽的スキームは，次で与えられる： \begin{align*} & \frac{u_i^{n+1}-u_i^{n}}{\tau}=\kappa \frac{u_{i-1}^n-2u_{i}^n+u_{i+1}^n}{h^2} && (0\le i\le N,\ n\ge 0)\\ & u_{-1}^n=u_1^n,\ u_{N+1}^n=u_{N-1}^n && (n\ge 1)\\ & u_i^0=a({x}_i) && (0\le i\le N+1). \end{align*} 陽的差分スキームを行列とベクトルで表現すると， \[ \frac{1}{\tau}[\boldsymbol{u}^{(n+1)}-\boldsymbol{u}^{(n)}]=-\frac{k}{h^2} A' \boldsymbol{u}^{(n)} \quad (n\ge 1),\qquad \boldsymbol{u}^{(0)}= \boldsymbol{a}, \] すなわち， \[ \boldsymbol{u}^{(n)}=(I-\lambda A') \boldsymbol{u}^{(n-1)} \quad (n\ge 1),\qquad \boldsymbol{u}^{(0)}=\boldsymbol{a} \] となる．ただし， $\boldsymbol{u}^{(n)}=(u_0^n,\ldots,u_N^n)\in\mathbb{R}^{N+1}$， $\boldsymbol{a}=(a(x_0),\ldots,a(x_{N}))\in\mathbb{R}^{N+1}$ と定義している．さらに， \begin{equation*} A'=\begin{pmatrix} 2 &-2 &0 &\cdots &0\\ -1 &2 &-1 &\cdots &\\ & &\ddots &\ddots &\\ & \cdots&-1 &2 &-1\\ 0 &\cdots & 0 &-2 &2 \end{pmatrix} \in\mathbb{R}^{(N+1)\times (N+1)} \end{equation*} とした．

同じように考えれば，陰的 $\theta$ スキームは， \begin{equation} \tag{B.6} {H}_{\theta\lambda}' \boldsymbol{u}^{(n)}=K_{(1-\theta)\lambda}'\boldsymbol{u}^{(n-1)} \quad (n\ge 1),\qquad \boldsymbol{u}^{(0)}=\boldsymbol{a} \end{equation} となる．ここで， \[ {H}_{\theta\lambda}'=I+\theta\lambda A' ,\quad K_{(1-\theta)\lambda}'=I-(1-\theta)\lambda A' \] とおいている．

これはこれで良いのだが， 行列 $A'$，したがって，${H}_{\theta\lambda}'$ も $K_{(1-\theta)\lambda}'$ も非対称である．一方で，もともとの，初期値境界値問題 (A.1a)，(B.5)，(A.1c)には，このような「非対称性」はない．（何をもって「対称」と言うのかを定義していないので，ボンヤリした話になってしまっていることを許してください．） この意味で，(B.6)は悪くはないが，少々，筋が悪いように思われる．

そこで，次のようにしてみる．上と同じ $h$ を使って， $\hat{x}_i=\left(i-\frac12\right)h$ とおき， 格子点 $(\hat{x}_i,t_n)$ $(0\le i\le N+1, n\ge 0)$ を考えるのである． $\hat{x}_0=-h/2$ と $\hat{x}_{N+1}=1+h/2$ は仮想格子点である． 初期値境界値問題(A.1a)，(B.5)，(A.1c)の解 $u$ について，格子点 $(\hat{x}_i,t_n)$ 上での近似値 $u_i^n$ を求めたい．

図B.3
図B.3

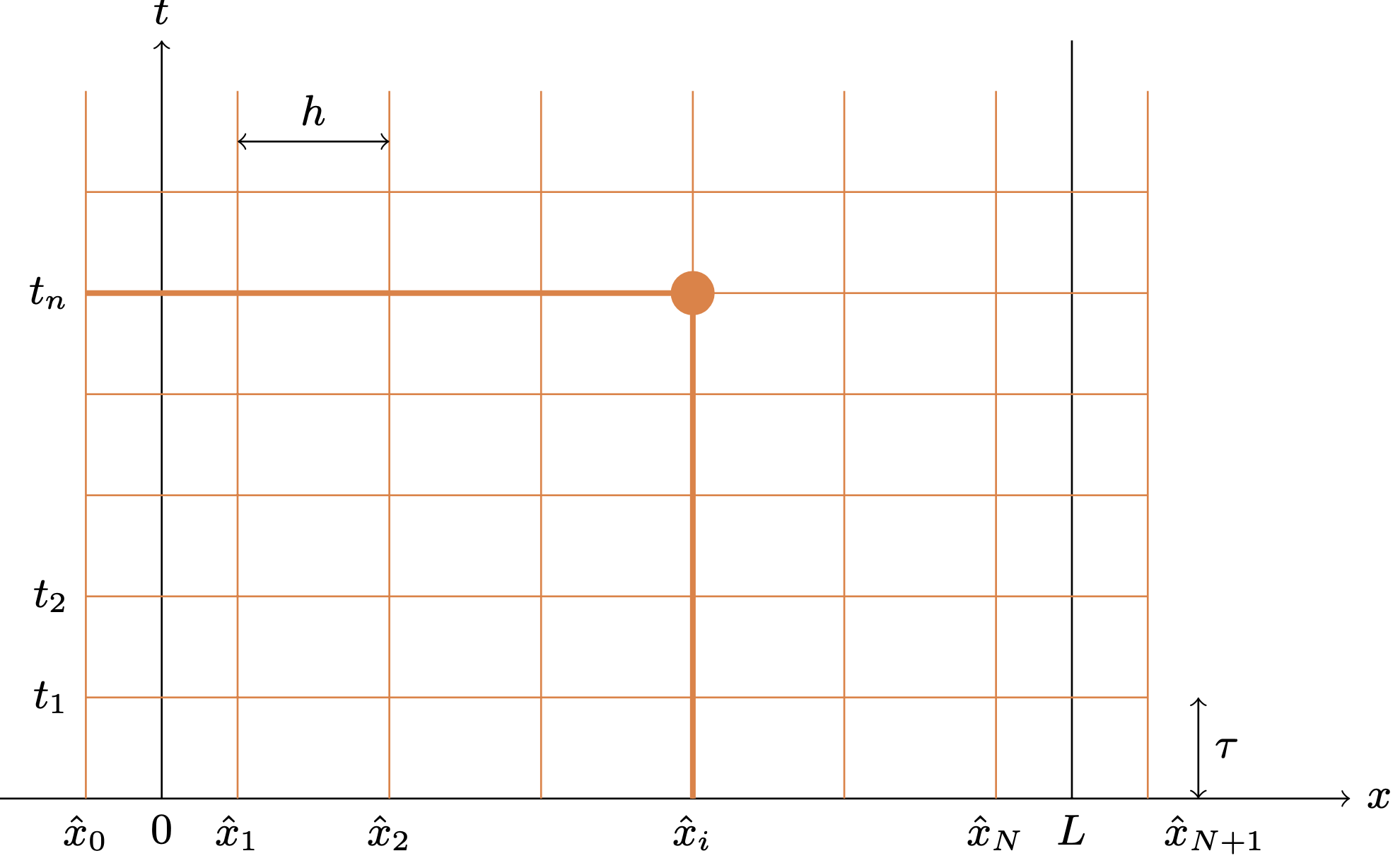
陽的スキームは， \begin{equation*} \frac{u_i^{n+1}-u_i^{n}}{\tau}=\kappa \frac{u_{i-1}^n-2u_{i}^n+u_{i+1}^n}{h^2} \qquad (1\le i\le N,\ n\ge 0) \end{equation*} となる．形としては前と同じであるが，$x$ について近似を求めている場所が異なる．そして， $i=1,N$ とした際に現れる $u_{0}^n$ と $u_{N+1}^n$ を，Neumann境界条件(B.5)を用いて消去する．すなわち，$(\partial u/\partial x)(0,t)=0$ を，$x=0$ を中心として中心差分商で近似する．具体的には， \[ \frac{u(\hat{x}_{1},t)-u(\hat{x}_{0},t)}{h}\approx 0 \] と考える．したがって，$u_0^N$ は，$\frac{u_{1}^{n}-u_0^n}{h}=0$，つまり，$u_{0}^{n}=u_1^n$ と定めるのが自然であろう．同様に，$u_{N+1}^n=u_{N}^n$ とすれば良い．

結果として，陽的差分スキームは，次で与えられる： \begin{alignat*}{2} & \frac{u_i^{n+1}-u_i^{n}}{\tau}=\kappa \frac{u_{i-1}^n-2u_{i}^n+u_{i+1}^n}{h^2} &\quad& (1\le i\le N,\ n\ge 0)\\ & u_0^n=u_1^n,\ u_{N+1}^n=u_N^n && (n\ge 1)\\ & u_i^0=a(\hat{x}_i) && (0\le i\le N+1). \end{alignat*} これは， \[ \boldsymbol{u}^{(n)}=(I-\lambda B) \boldsymbol{u}^{(n-1)} \quad (n\ge 1),\qquad \boldsymbol{u}^{(0)}=\boldsymbol{a} \] となる．ただし， $\boldsymbol{u}^{(n)}=(u_1^n,\ldots,u_N^n)\in\mathbb{R}^{N}$， $\boldsymbol{a}=(a(\hat{x}_1),\ldots,a(\hat{x}_{N}))\in\mathbb{R}^{N}$ と定義し直した上で， \begin{equation} B= \begin{pmatrix} 1 &-1 &0 &\cdots &0\\ -1 &2 &-1 &\cdots &\\ & &\ddots &\ddots &\\ & \cdots&-1 &2 &-1\\ 0 &\cdots & 0 &-1 &1 \end{pmatrix} \in\mathbb{R}^{N\times N} \end{equation} としている．同じように考えれば，単純陰的スキームは， \[ ({I}+\lambda B) \boldsymbol{u}^{(n)}=\boldsymbol{u}^{(n-1)} \quad (n\ge 1),\qquad \boldsymbol{u}^{(0)}=\boldsymbol{a} \] となり，$0\le \theta\le 1$ に対して，陰的 $\theta$ スキームは， \begin{equation} \tag{B.7} {D}_{\theta\lambda} \boldsymbol{u}^{(n)}=E_{(1-\theta)\lambda}\boldsymbol{u}^{(n-1)} \quad (n\ge 1),\qquad \boldsymbol{u}^{(0)}=\boldsymbol{a} \end{equation} で与えられる．ここで， \[ {D}_{\theta\lambda}=I+\theta\lambda B ,\quad E_{(1-\theta)\lambda}=I-(1-\theta)\lambda B \] とおいている． 

In [23]:  
#（斉次）熱方程式、零Neumann境界条件、陰的thetaスキーム（行列・ベクトル形式、CSCを使う）
def heat_0nbc_theta1(L, kappa, initial, N, T, lam, theta, num):
    
  h = L/N
  tau = lam*h*h/kappa
  nmax = int(T/tau)
  step=int(max(1, nmax/num))
  
  B = 2.0*np.diag(np.ones(N)) - np.diag(np.ones(N-1), 1) - np.diag(np.ones(N-1), -1)
  B[0,0] = 1.0
  B[-1,-1] = 1.0
  D = csc_matrix(np.eye(N, N) + theta * lam * B)
  E = csc_matrix(np.eye(N, N) - (1.0 - theta) * lam * B)
  LU = splu(D)  # LU分解

  xx = np.linspace(0, L, N+1) 
  x = 0.5*(xx[1:]+xx[:-1])
  tgrid = np.array([0.0])
  u = np.vectorize(initial)(x)
  sol=np.copy(u)

  for n in range(nmax):
    tnow = (n+1)*tau
    u = LU.solve(E.dot(u)) # 連立一次方程式の解法 CSC 版
    if (n+1)%step==0.0:
      sol = np.vstack((sol,u))
      tgrid = np.append(tgrid, tnow)
    
  return x, tgrid, sol

$a(x)=4x^2(1-x)^2$ に対して，計算を実行しよう．$\theta=1/2$ とする．また， 最終時刻での，数値解 の最大値と最小値も出力する．

In [24]:  
# 初期値
def initial3(x):
  return 4.0*x**2*(1.0-x)**2

#パラメータの設定
L = 1.0
kappa = 1.0
N = 51
T = 1.0
lam = 0.4
num = 60

#熱方程式の計算
theta = 1.0
x, tn, sol = heat_0nbc_theta1(L, kappa, initial3, N, T, lam, theta, num)

#結果の表示
print('final time =',tn[-1])
print('umax =',np.amax(sol[-1,:]))
print('umin =',np.amin(sol[-1,:]))

#図の表示
plot_solution(x, sol)

#アニメーションを表示
anim = plot_animation(x, tn, sol)
#結果をheat.gifに保存（Googleドライブをマウントしておくこと！）
anim.save('/content/drive/MyDrive/Colab Notebooks/fig/heat_nbc.gif', writer='pillow')
rc('animation', html='jshtml')
plt.close()
anim
  
Out [24]: 
final time = 0.9965397923875431
umax = 0.1333333505785685
umin = 0.13333335057856704
図2.3
図B.4a Out [24]
図B.3
図B.4b Out [24]

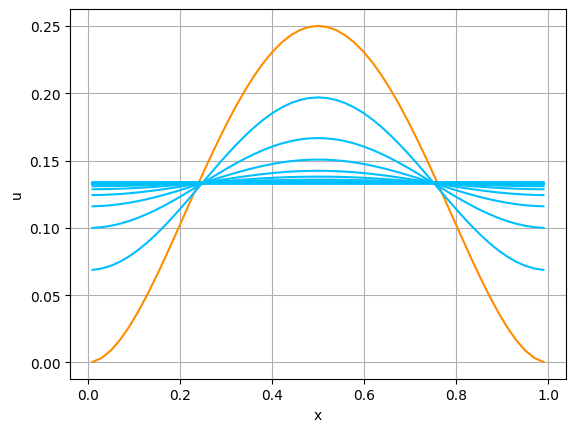
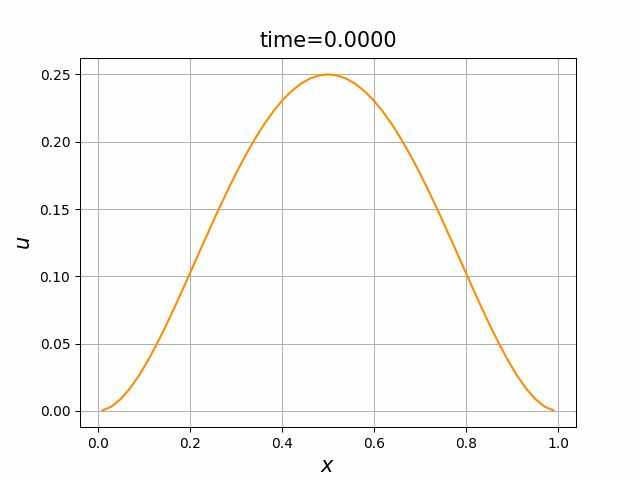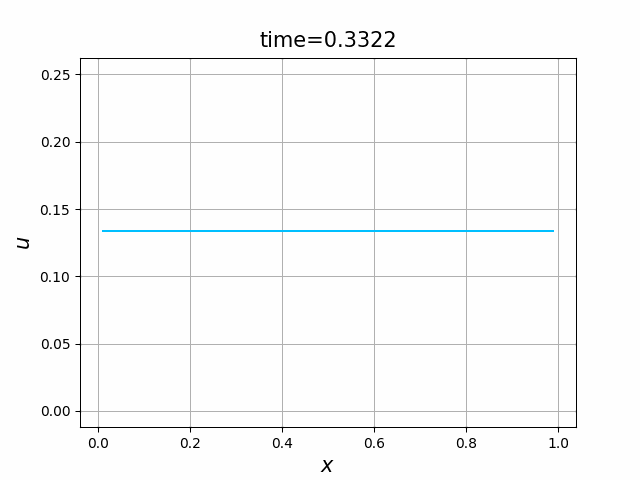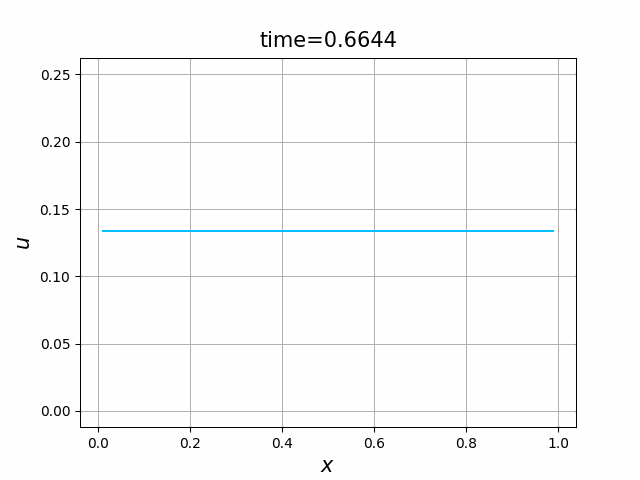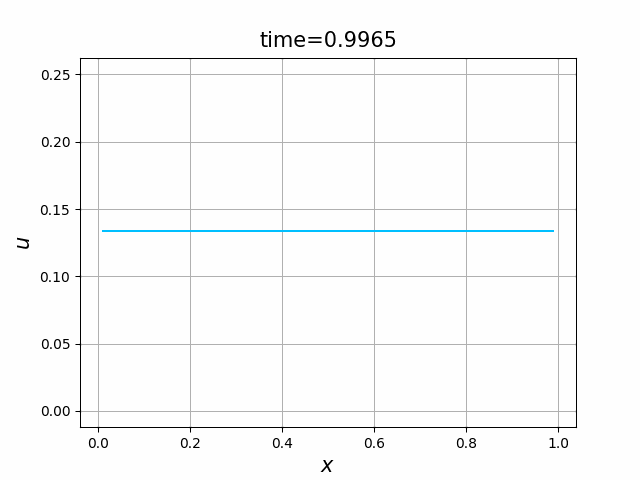
この結果を見ると，数値解は，各 $i$ において， $u_i^n\to 0.1333$ $(n\to \infty)$ となっていることが観察できる．実は，(A.1a)，(B.5)，(A.1c)の解は， \begin{align*} \frac{d}{dt}\int_0^L u(x,t)~dx &= \int_0^L \frac{\partial}{\partial t}u(x,t)~dx \\ &= \int_0^L \kappa \frac{\partial^2}{\partial x^2}u(x,t)~dx \\ &=\kappa \left[\frac{\partial u}{\partial x}(x,t)~\right]_{x=0}^{x=L} =0, \end{align*} すなわち， \[ \int_0^L u(x,t)~dx= \int_0^L a(x)~dx\qquad (t\ge 0) \] を満たす．実際，今の場合， \[ \int_0^1 4x^2(1-x)^2~dx=\frac{2}{15}=1.3333\cdots \] である．

非線形反応拡散方程式

ある地域に生息する生物の個体群密度 $\mathcal{N}=\mathcal{N}(t)$ の時間変化を記述する数理モデルとして ロジスティック方程式 \[ \frac{d\mathcal{N}}{dt}= \varepsilon (1-\mathcal{N})\mathcal{N} \] が知られている．$\varepsilon$ は正の定数である．これは，マルサスの法則 $d\mathcal{N}/dt=\alpha \mathcal{N}$ において， 増殖係数 $\alpha$ が，個体数の増加による環境の悪化を反映して $\mathcal{N}$ に応じて $\alpha=\varepsilon(1-\mathcal{N})$ のように変化する現象を表現している．実際，初期値が $(0 < )\mathcal{N}(0) < 1$ であるならば，解 $\mathcal{N}(t)$ は $t$ に関して単調に増加し，$\mathcal{N}(t)\to 1$ $(t\to\infty)$ となる．すなわち，ロジスティック方程式は飽和現象の単純な数理モデルになっている．それでは， 生物の空間的な広がりを考慮し，生物がランダムに運動している場合は，この生物の長時間的な挙動はどうなるであろうか．それを考えるために，次の初期値境界値問題を考えよう： \begin{align} & \frac{\partial u}{\partial t}=\kappa \frac{\partial^2 u}{\partial x^2} +\varepsilon (1-u)u && (0 < x < 1,\ t > 0) \tag{B.8a}\\ & u(0,t)=0,\ u(1,t)=0 && (t > 0) \tag{B.8b}\\ & u(x,0)=a(x) && (0\le x\le 1).\tag{B.8c} \end{align} ここで，$\kappa$ は正の定数，$a=a(x)$ は， \begin{equation*} a\not\equiv 0, \quad 0\le a(x)\le 1\ (0\le x\le 1),\quad a(0)=a(1)=0 \end{equation*} を満たす $[0,1]$ 上の連続関数とする．

せっかく陰的スキームを勉強したが，この初期値境界値問題に対しては，陽的スキームを適用しよう（理由はわかりますね？）． 前回，(A.13)を導入した時と同じ記号を用いる（ただし，$L=1$ とする）． 差分スキームは， \begin{align} &\frac{u_i^{n+1}-u_i^n}{\tau}=\kappa \frac{u_{i-1}^{n}-2u_i^{n}+u_{i+1}^n}{h^2} +\varepsilon (1-u_i^n)u_i^n&& (1\le i\le N,\ n\ge 0) \tag{B.9a},\\ & u_0^n=u_{N+1}^n=0 && (n\ge 1), \tag{B.9b}\\ & u_i^0=a(x_i) && (0\le i\le N+1)\tag{B.9c} \end{align} とすれば良い．プログラムも，前に作った，非斉次熱方程式を計算するプログラムを少し修正すれば良いのみである．

In [25]:  
#非線形反応拡散方程式（ロジスティック）、零Dirichlet境界条件、陽的スキーム
def heat_logistic(L, kappa, initial, ep, N, T, lam, num):
    
  h = L/(N+1)
  tau = lam*h*h/kappa
  nmax = int(T/tau)
  step=int(max(1, nmax/num))
  
  xgrid=np.linspace(0.0, L, N+2)
  tgrid=np.array([0.0])
  u=np.vectorize(initial)(xgrid)
  sol=np.copy(u)
  
  n=0
  tnow=n*tau
  for n in range(nmax):
    u[1:N+1] = (1-2*lam)*u[1:N+1]+lam*(u[0:N]+u[2:N+2]) + tau*ep*u[1:N+1]*(1.0-u[1:N+1])
    tnow = (n+1)*tau
    if (n+1)%step==0:
      sol=np.vstack((sol,u))
      tgrid=np.append(tgrid, tnow)

  return xgrid, tgrid, sol

$\lambda=0.4$ を固定して， $\kappa$ と $\varepsilon$ の値を色々変えて，計算してみる．（$T$ の値は適当に設定する．） 

In [26]:  
# 初期値
def initial4(x):
  return x*np.sin(3.0*np.pi*x)**2
  
#パラメータの設定
L = 1.0
kappa = 10.0
ep = 10.0
N = 101
T = 0.3
lam = 0.4
num = 60

#熱方程式の計算
x, tn, sol = heat_logistic(L, kappa, initial4, ep, N, T, lam, num)

#図の表示
plot_solution(x, sol)

#アニメーションを表示
anim = plot_animation(x, tn, sol)
#結果をheat.gifに保存（Googleドライブをマウントしておくこと！）
anim.save('/content/drive/MyDrive/Colab Notebooks/fig/logistic.gif', writer='pillow')
rc('animation', html='jshtml')
plt.close()
anim
図B.3
図B.5a In [26]，$\kappa =10$，$\varepsilon=10$，$\lambda=0.4$，$T=0.3$
図B.3
図B.5b In [26]，$\kappa =5$，$\varepsilon=10$，$\lambda=0.4$，$T=0.3$
図B.3
図B.5c In [26]，$\kappa =1$，$\varepsilon=10$，$\lambda=0.4$，$T=1$
図B.3
図B.5d In [26]，$\kappa =0.1$，$\varepsilon=10$，$\lambda=0.4$，$T=2$

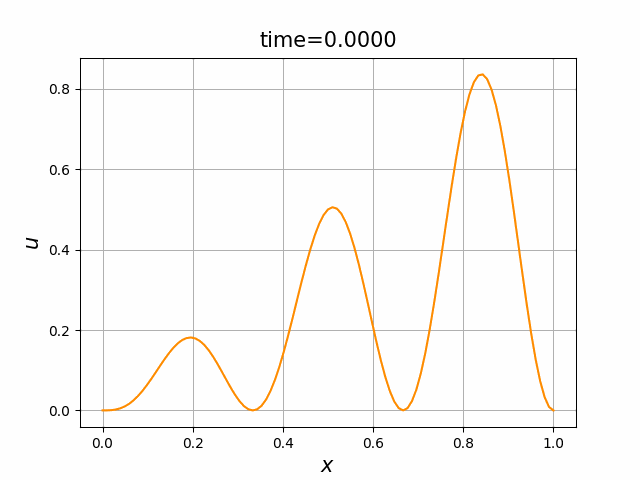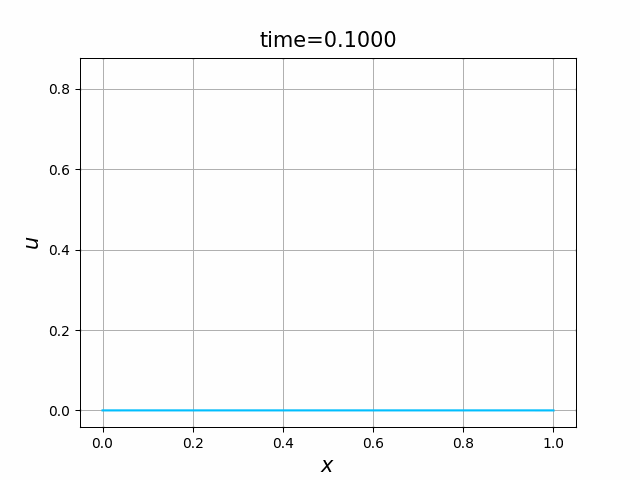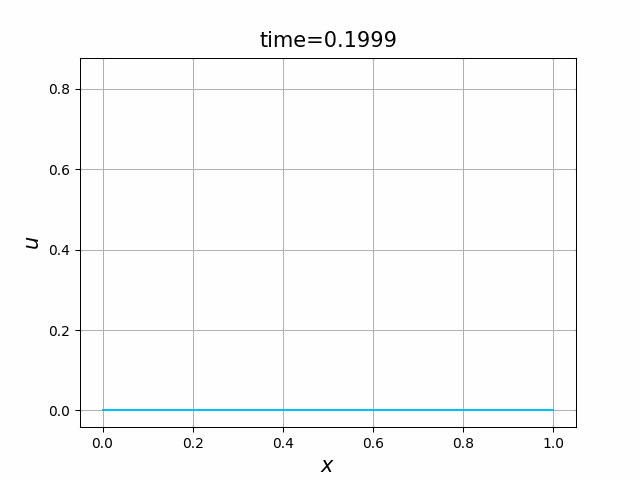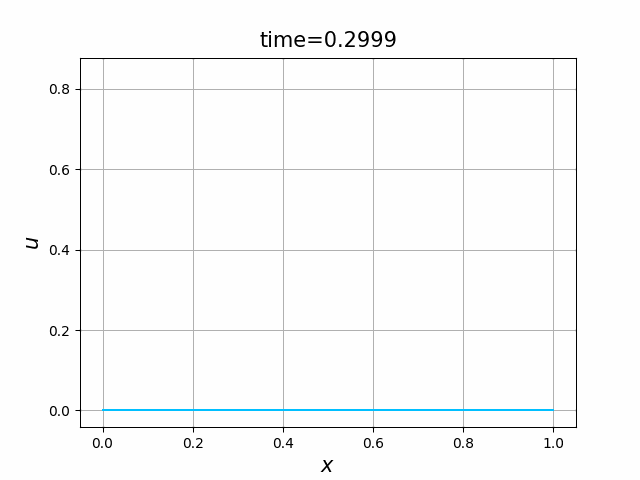
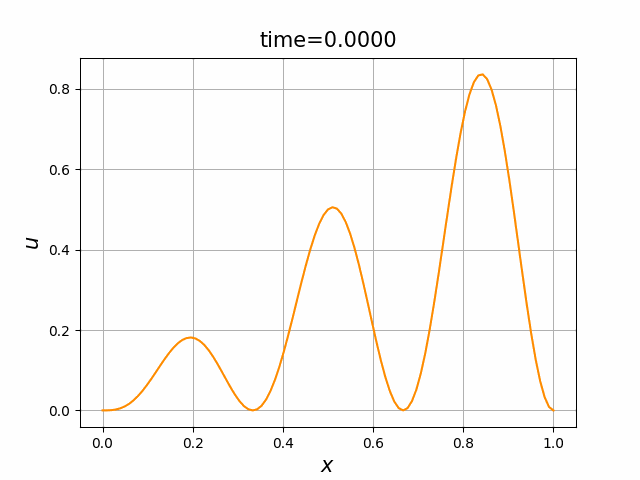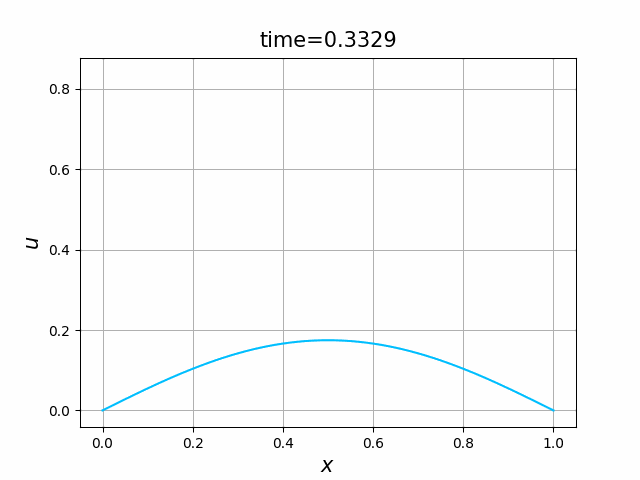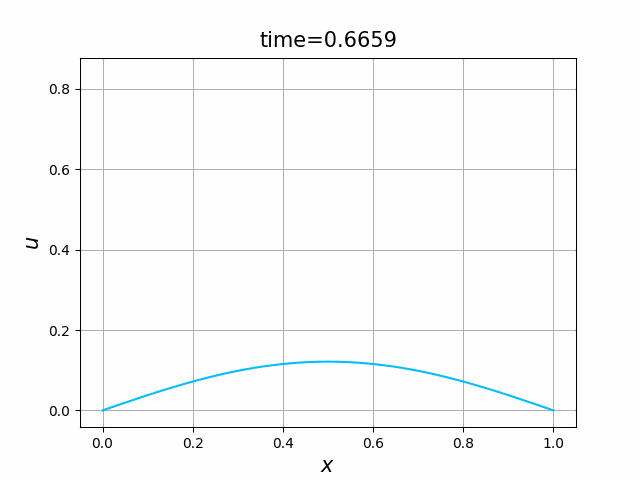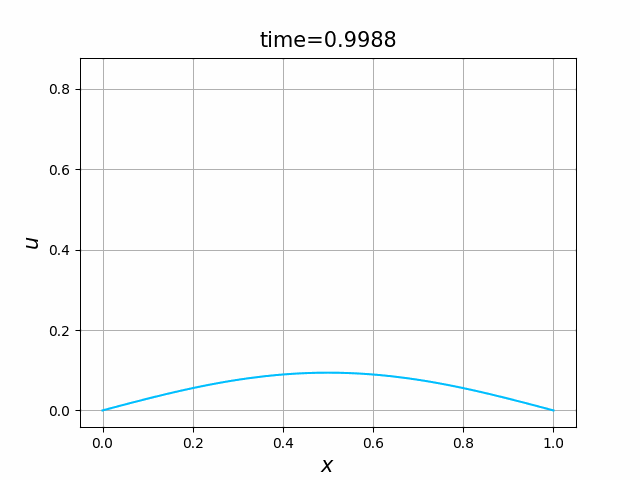
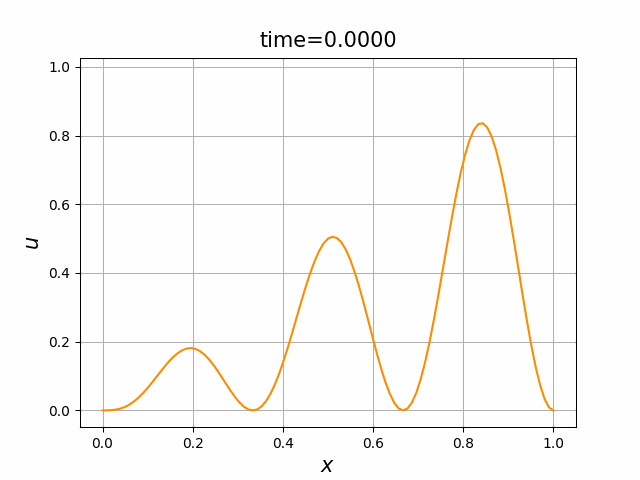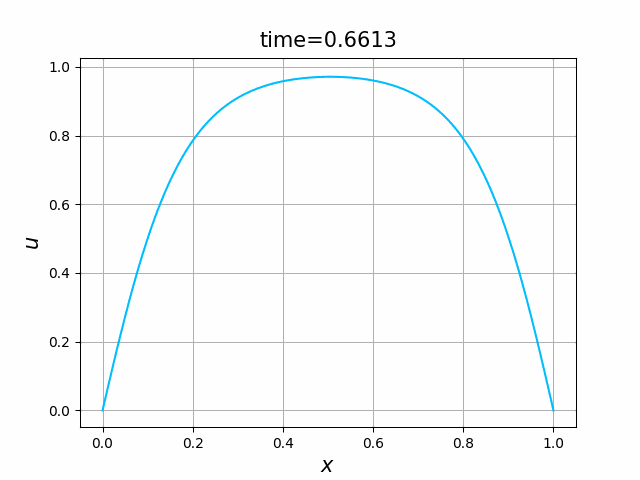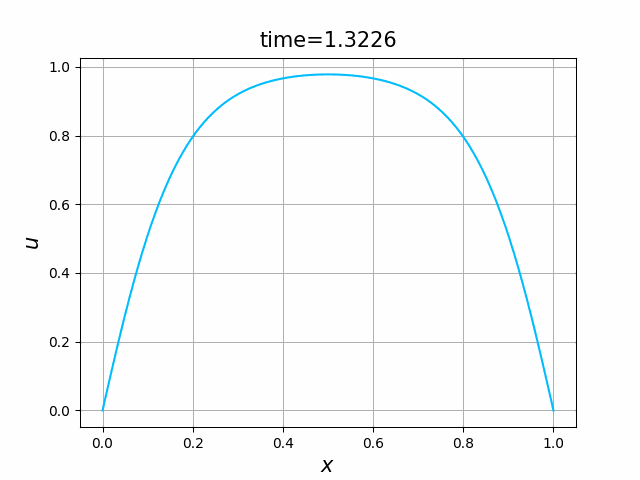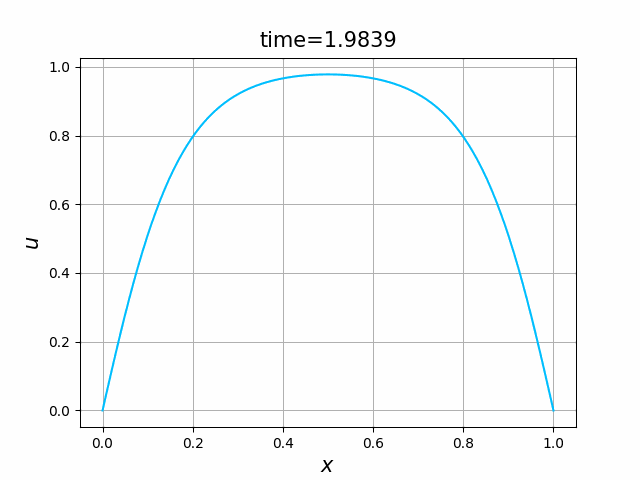
実は，(B.8a,b,c)の解 $u$ について，次のことが知られている（例えば，[亀高]を見よ）：

  1. 初期値境界値問題(B.8a,b,c)には，$[0,1]\times [0,\infty)$ 上で唯一の（古典）解$u=u(x,t)$が存在し，この $u$ は， \begin{equation*} 0\le u(x,t)\le 1\qquad (0\le x\le 1,\ t\ge 0) \end{equation*} を満たす．
  2. $\varepsilon \le \kappa\pi^2$ ならば，$u$ は，$t\to\infty$ のとき，定数関数 $0$ に $0\le x\le 1$ で一様に収束する．
  3. $\varepsilon > \kappa \pi^2$ ならば， \begin{gather} 0=\frac{d^2 w}{d x^2} +\varepsilon (1-w)w \quad (0 < x < 1) ,\tag{B.9a}\\ w(0)=w(1),\qquad w\ge 0,\qquad w\not\equiv 0 \tag{B.9b} \end{gather} を満たす関数 $w=w(x)$ が唯一存在し，$u$ は，$t\to\infty$ のとき，関数 $w$ に $0\le x\le 1$ で一様に収束する．
図B.5a,b,c,dで観察した事実は，この結果と整合している．

しかしながら，$\lambda=0.5$ を用いて，それ以外は，図B.5dの計算と同じ条件 $\kappa =0.1$，$\varepsilon=10$，$T=2$ で計算した結果が，図B.6である．

図B.6
図B.6 In [26]，$\kappa =0.1$，$\varepsilon=10$，$\lambda=0.5$，$T=2$

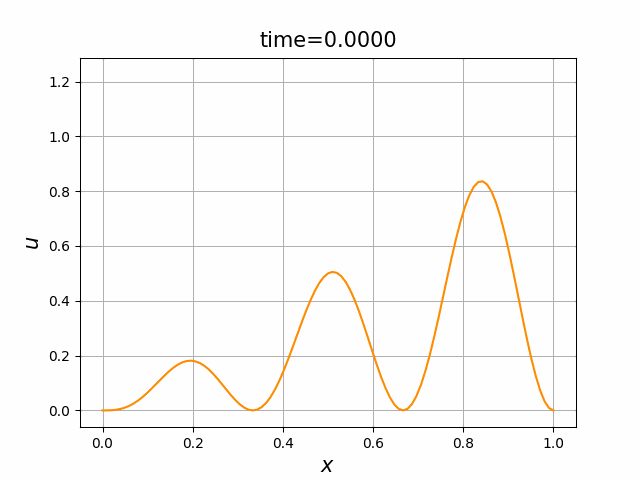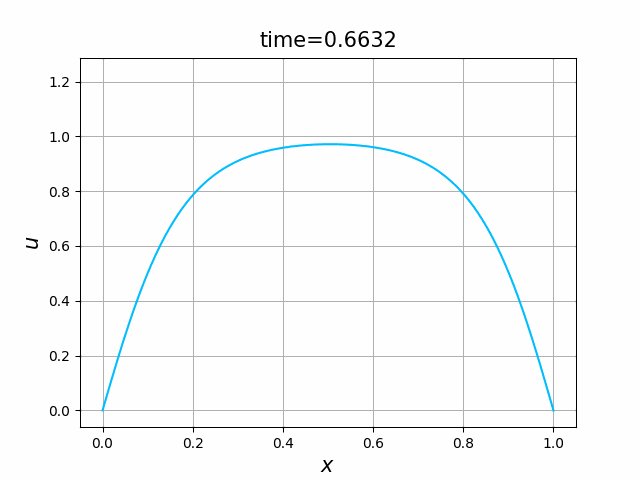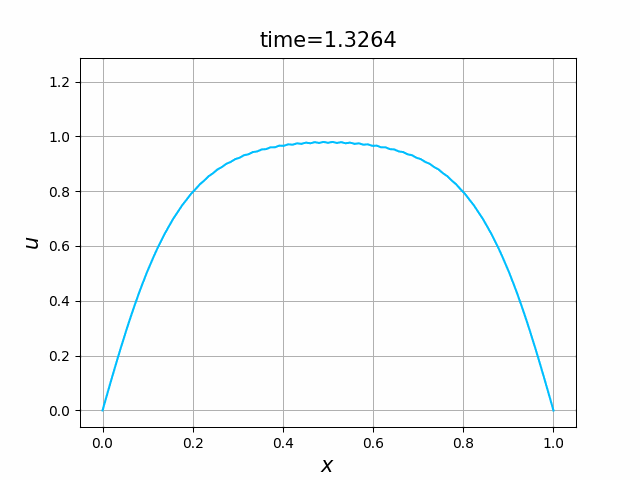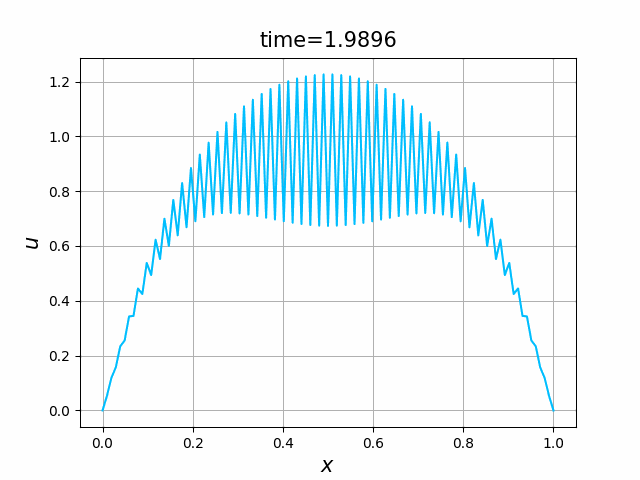
$\lambda=0.5$ は，熱方程式の安定性・収束性のための十分条件 $\lambda\le 1/2$ を満たしている．にもかかわらず，差分スキームの解は，数値的に不安定性になる．

実は，陽的差分スキーム(B.9a,b,c)の解 $u_i^n$ について，次のことが知られている（例えば，[三村]，[齊藤2023]を見よ）：

  1. $\varepsilon$，$\tau$，$\lambda$ に対して， \begin{equation} \tag{B.10} 1-\varepsilon \tau -2\lambda\ge 0 \end{equation} を仮定すると，(B.9a,b,c)の解 $u_i^n$ は \begin{equation*} 0\le u_i^n\le 1\qquad (1\le i\le N,\ n\ge 0) \end{equation*} を満たす．
  2. さらに，同じ条件の下で，誤差は \begin{equation*} \max_{0\le t_n\le T}\|\boldsymbol{e}^{(n)}\|_\infty\le \frac{e^{\varepsilon T}-1}{\varepsilon} (\tau + h^2)\mathcal{M} \end{equation*} を満たす．

問題

  1. 上記の入力と出力をすべて確かめよ．
  2. パラメータ値を変えて，計算を再試行せよ．
  3. 例題を自分で設定して，上記の方法を試せ．

課題

課題B.1

熱方程式の初期値境界値問題(A.1a,b,c)に対する陰的 $\theta$ スキーム(B.4)について， $\theta=1$ と $\theta=1/2$ の場合を考える． まず，十分大きな $N$ を固定して，$h=L/(N+1)$ とする．次に，$\tau$ を， $\lambda=\kappa\tau/h^2$ から求めずに，正の整数 $N_y$ を採り $\tau=T/N_y$ とする． そして，$N_y$ の値を変化させることで， $\theta=1$ のときは，誤差が$O(\tau)$で， $\theta=1/2$ のときは，誤差が$O(\tau^2)$で減衰することを数値計算で確認せよ．

課題B.2

Neumann境界条件(B.5)と初期条件(A.1c)の下で，非斉次の熱方程式 \begin{equation} \tag{A.12} \frac{\partial u}{\partial t}=\kappa \frac{\partial^2 u}{\partial x^2}+f\qquad (0 < x < L,~ t > 0) \end{equation} を考える．この初期値境界値問題に対して，陰的 $\theta$ 法を導入して，（$h$ を変化させたときの ）その誤差の挙動を観察せよ．（2種類の差分スキームを説明したが，どちらを用いても良い．）

課題B.3

非線形熱方程式 \begin{align} & \frac{\partial u}{\partial t}=\kappa \frac{\partial^2 u}{\partial x^2} +e^u && (0 < x < 1,\ t > 0) \\ & u(0,t)=0,\ u(1,t)=0 && (t > 0) \\ & u(x,0)=a(x) && (0\le x\le 1). \end{align} に対して，陽的差分スキームを導出せよ． 初期値を $a(x)=\sin(\pi x)$ とし，$\kappa$ を $0.2 \le \kappa \le 0.3$ の範囲で変えて計算し，差分スキームの解 $u_i^n$ について，$t_n\to \infty$ の際の挙動を観察せよ．$\kappa$ の値によって，どのような違いがあるかを調べよ．さらに．別の初期関数を用いて，同様の観察せよ．

ヒント1: $u_i^n\to \infty$ となってしまうとき，値が大きくなりすぎると，描画ができなくなるので，$T$ の値を，うまく調整すること．

ヒント2: [Fujita]の結果を参照せよ（これは短い論文なので，読むのはそう難しくない）．[Fujita]では，$\kappa=1$ を固定して，微分方程式を考える領域（区間）を変化させている． これは，適当に変数変換をすれば，区間を $0\le x\le 1$ に固定して，$\kappa$ の値を変化させることと同じでる．

参考文献