2025-3A 数理情報学（東京大学教養学部） [齊藤宣一] [top] [A] [B] [C] [UTOL]

B. 線形移流方程式の差分解法

定数係数の場合

斉次の線形移流方程式の初期値問題 \begin{align} u_t+cu_x&=0, && (x,t)\in \mathbb{T}\times (0,T),\tag{B.1a}\\ u(x,0)&={a}(x), && x\in \mathbb{T}\tag{B.1b} \end{align} を考える．ただし，$\mathbb{T}=\mathbb{R}/\mathbb{Z}$ としている．

$0 < N,m\in\mathbb{Z}$ を取り，$h=1/N$，$\tau=T/M$， $x_i=ih$，$t_n=n\tau$ とする．$u^n_i\approx u(x_i,t_n)$ が求めるべき近似解である．以下，何も断らなくても， \[ u_{i+N}^n=u_{i}^n \] とする．

(B.1)に対する最も素朴な差分スキームは， \begin{equation*} \frac{u^{n+1}_i-u^n_i}{\tau}+c\frac{u_{i+1}^n-u_{i-1}^n}{2h}=0, \end{equation*} すなわち， \begin{equation} \tag{B.2} \lambda \stackrel{\textrm{def.}}{=}c\frac{\tau}{h} \end{equation} とおいて， \begin{equation} \tag{B.3} u^{n+1}_i=u^n_i-\frac{1}{2}\lambda (u_{i+1}^n-u_{i-1}^n) \end{equation} である．これを中心差分スキームと呼ぶ．初期条件は， \begin{equation} \tag{B.4} u^{0}_i={a}(x_i) \end{equation} とする（このことは，以後，いちいち断らない）．

さらに， \begin{equation} \tag{B.5} \lambda_{\textup{abs}} \stackrel{\textrm{def.}}{=}|\lambda|=|c|\frac{\tau}{h} \end{equation} とおく．

利用予定のモジュールを最初にまとめてインポートしておく．

In [1]:  
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import animation, rc
from IPython.display import HTML

In [2]:  
from google.colab import drive
drive.mount('/content/drive')

可視化のためのプログラムは，前回までと同じものを使う．

In [3]:  
#図のプロット、一枚の図に、グラフを重ねる
def plot_solution(xgrid, uvect):
  # 描画に関するパラメータの設定
  umax = np.max(sol)
  umin = np.min(sol)
  ulength = umax - umin
  umax += 0.05 * ulength
  umin -= 0.05 * ulength
  # t = 0                  
  plt.plot(xgrid,uvect[0,:],color='#ff8c00')
  # t > 0
  for n in range(1,uvect.shape[0]):
    plt.plot(xgrid,uvect[n,:],color='#00bfff')
  
  plt.xlabel('x')
  plt.ylabel('u')
  plt.ylim(umin, umax)
  plt.grid('on')
  plt.show()

In [4]:  
#アニメーションの作成
# IPython.displayモジュールを使う
def plot_animation(xgrid, tgrid, uvect):
  # 描画に関するパラメータの設定
  umax = np.max(sol)
  umin = np.min(sol)
  xmax = np.max(xgrid)
  xmin = np.min(xgrid)
  ulength = umax - umin
  utop = umax + 0.1*ulength
  umax += 0.05*ulength
  umin -= 0.05*ulength
  xmid = (xmax+xmin)/2
  xlength = xmax - xmin
  xmax += 0.05*xlength
  xmin -= 0.05*xlength
  
  # fig, axオブジェクトを作成
  fig, ax = plt.subplots()
  ims = []
  
  # t = 0
  n = 0
  im, = ax.plot(xgrid, uvect[n, :], color='#ff8c00')
  title = ax.text(xmid, utop, f'time={tgrid[n]:.4f}', ha='center', va='center', fontsize=15)
  ims.append([im, title])
    
  # t > 0
  for n in range(1, uvect.shape[0]):
    im, = ax.plot(xgrid, uvect[n, :], color='#00bfff')
    title = ax.text(xmid, utop, f'time={tgrid[n]:.4f}', ha='center', va='center', fontsize=15)
    ims.append([im, title])
    
  # 各軸のラベル
  ax.set_xlabel(r"$x$", fontsize=15)
  ax.set_ylabel(r"$u$", fontsize=15)
  # グラフの範囲を設定
  ax.set_xlim([xmin, xmax])
  ax.set_ylim([umin, umax])
  ax.grid(True)

  # ArtistAnimationにfigオブジェクトとimsを代入してアニメーションを作成
  return animation.ArtistAnimation(fig, ims)

(B.3)を実行するために，次のような In [6] を用意する． In [6] では， $\mathrm{u}=(u_0^n,u_1^n,\ldots,u_{N-1}^n)\in\mathbb{R}^{N}$ に対して， \[ \mathrm{np.roll(u,-1)}=(u_1^n,u_2^n,\ldots,u_{N-1}^n,u_{0}^n),\quad \mathrm{np.roll(u,1)}=(u_{N-1}^n,u_0^n,\ldots,u_{N-2}^n) \] であることを利用して，(B.3)の $u_{i+1}^n-u_{i-1}^n$ の部分を計算している．In [5]を参照せよ．

In [5]:  
N=5
y=np.linspace(0, 1, N+1)
print(y)
print(np.roll(y,-1))
print(np.roll(y,1))

Out [5]: 
[0.  0.2 0.4 0.6 0.8 1. ]
[0.2 0.4 0.6 0.8 1.  0. ]
[1.  0.  0.2 0.4 0.6 0.8]

In [6]:  
#線形移流方程式に対する中心差分スキーム
def linear_advection_central(c, initial, N, T, abslam, num):
  L = 1.0
  h = L/N
  tau = abslam*h/np.abs(c)
  lam = c*tau/h
  nmax = int(T/tau)
  step = int(max(1, nmax/num))

  xgrid = np.linspace(0.0, L, N)
  xtmp = np.copy(xgrid[0:N-1])
  tgrid = np.array([0.0])
  u = initial(xtmp)
  sol = np.copy(np.append(u,u[0]))

  for n in range(nmax):
    u = u - 0.5*lam*(np.roll(u,-1)-np.roll(u,1))
    tnow = (n+1)*tau
    if (n+1)%step==0:
      sol=np.vstack((sol,np.append(u,u[0])))
      tgrid=np.append(tgrid, tnow)

  return xgrid, tgrid, sol

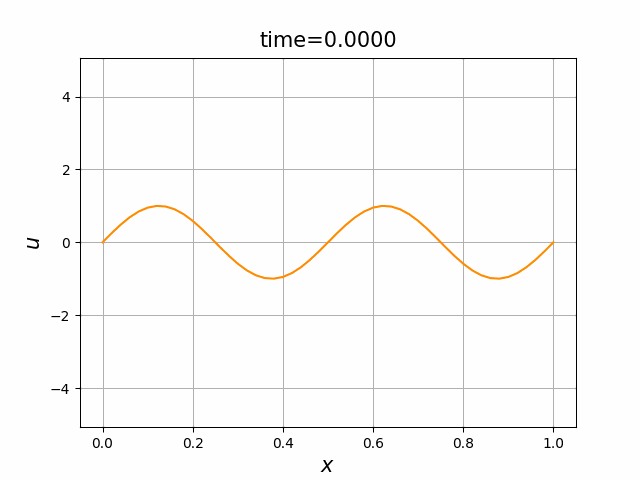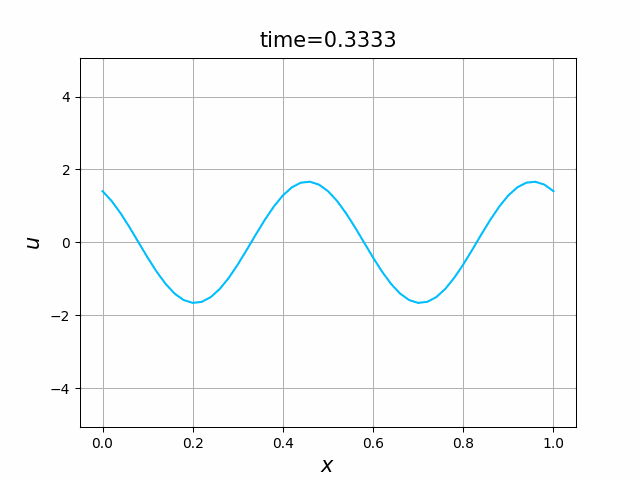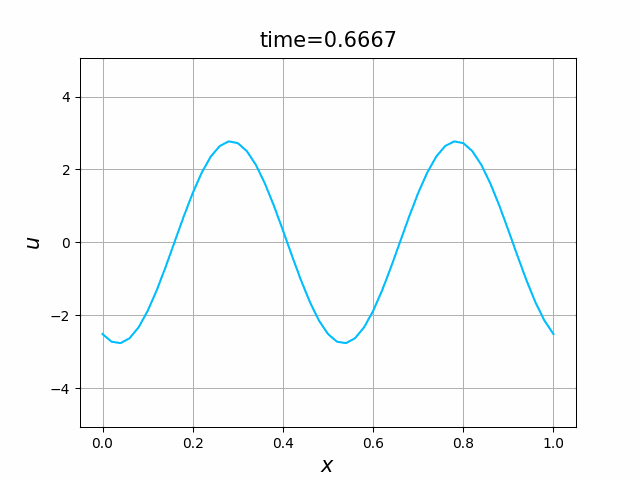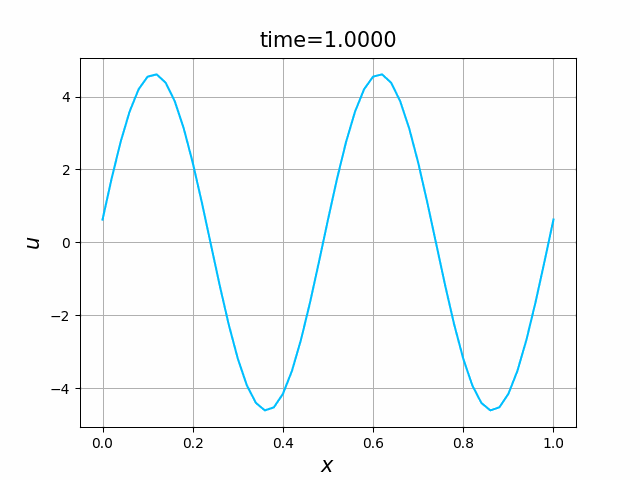
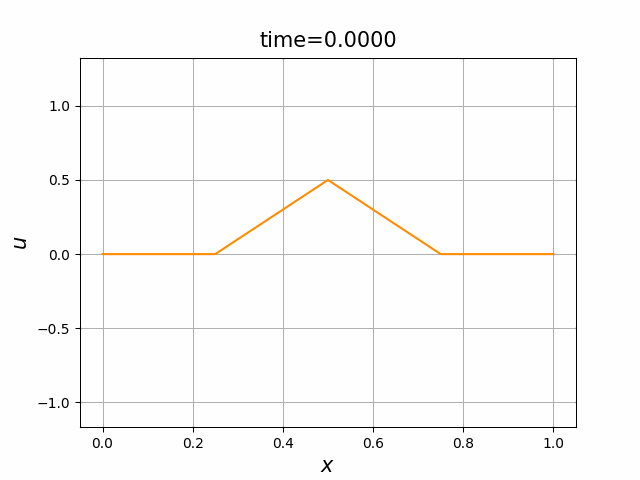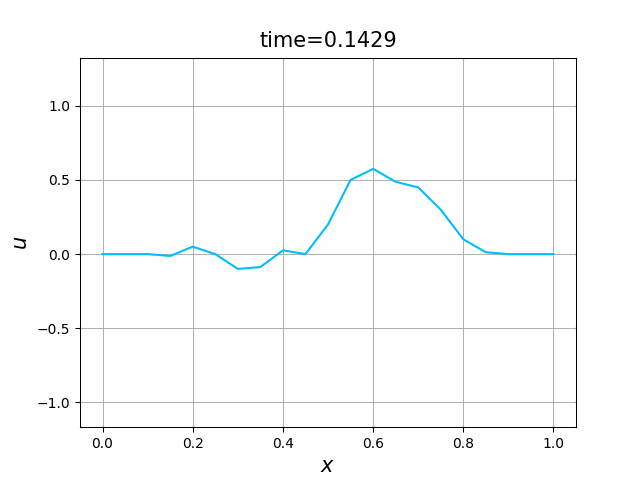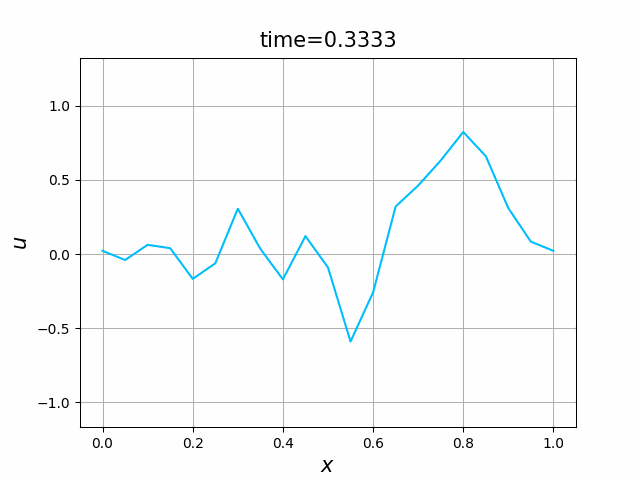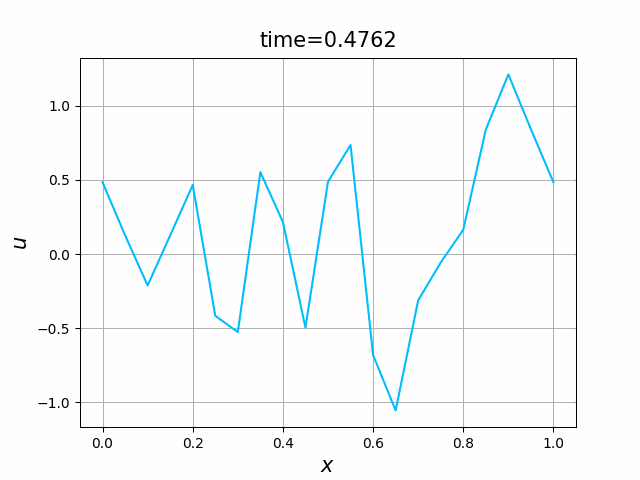
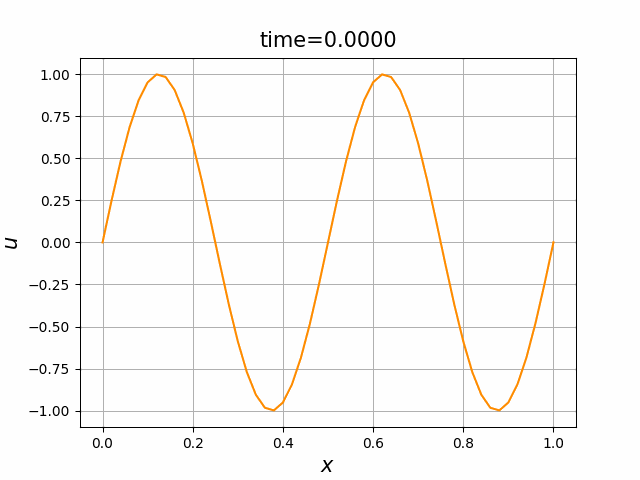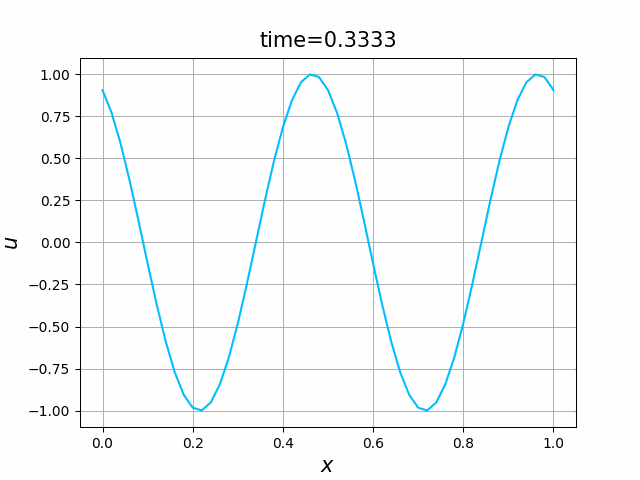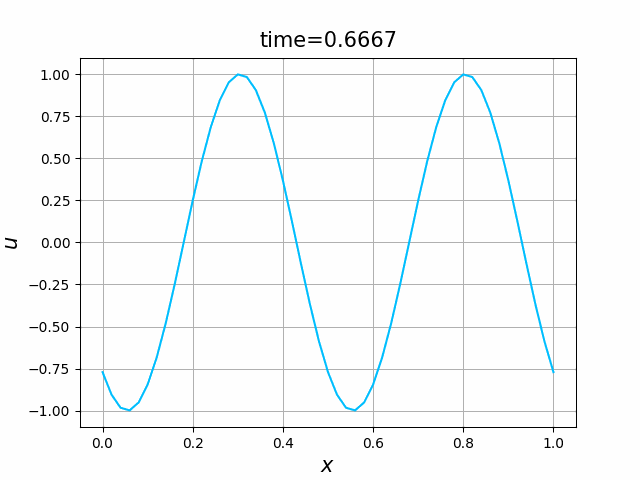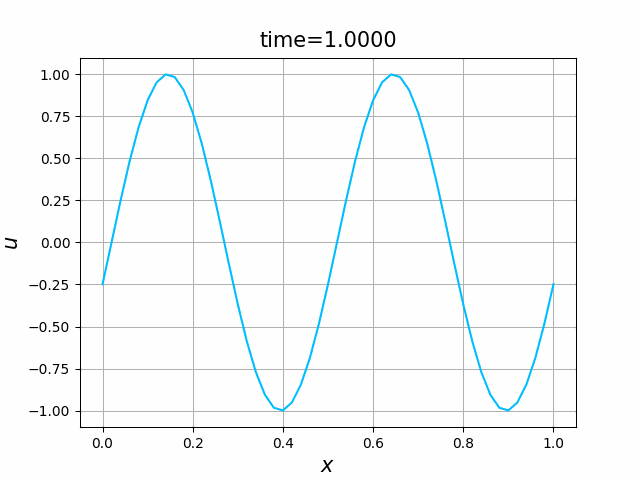
2つの初期関数 \begin{align} a_1(x)&=\sin(4\pi x),\tag{B.6a}\\ a_2(x)&=\max\{ 0, ~ \min\{2x-1/2, 3/2-2x\}\} \tag{B.6b} \end{align} について，In [6] を実行してみる． $c=1$ および $\lambda_{\textup{abs}}=1$ とする．図B.1が $a_1$，図B.2が $a_2$ を用いた計算結果である．

In [7]:  
# 初期値
def initial1(x):
  return np.sin(4*np.pi*x)

def initial2(x):
  return  np.maximum(0.0, np.minimum(2.0*x-0.5, 1.5-2.0*x))

#パラメータの設定
c = 1.0
N = 51
T = 1.0
abslam = 1.0
num = 40

#線形移流方程式の計算
x, tn, sol = linear_advection_central(c, initial1, N, T, abslam, num)

#図の表示
plot_solution(x, sol)

#アニメーションを表示
anim = plot_animation(x, tn, sol)
#結果をheat.gifに保存（Googleドライブをマウントしておくこと！）
anim.save('/content/drive/MyDrive/Colab Notebooks/fig/heat.gif', writer='pillow')
rc('animation', html='jshtml')
plt.close()
anim

(B.1)に対して，別の差分スキームを考えることができる．まず，$c > 0$ とする．この場合は，(B.1)を， \begin{equation*} \frac{u^{n+1}_i-u^n_i}{\tau}+c\frac{u_{i}^n-u_{i-1}^n}{h}=0, \end{equation*} すなわち， \begin{equation*} u^{n+1}_i=u^n_i-\lambda (u_{i}^n-u_{i-1}^n) \end{equation*} と近似する． $c < 0$ の場合は， \begin{equation*} u^{n+1}_i=u^n_i-\lambda (u_{i+1}^n-u_{i}^n) \end{equation*} とする．まとめると， \begin{equation} \tag{B.7} u_i^{n+1}= [1-\theta\lambda+(1-\theta)\lambda] u_i^n +\theta\lambda u_{i-1}^n -(1-\theta)\mu u_{i+1}^n,\quad \theta= \begin{cases} 1 &(c\ge 0)\\ 0 &(c< 0) \end{cases} . \end{equation} これを風上（upwind）差分スキームあるいは上流（upstream）差分スキームと呼ぶ．初期条件は，(B.4)と同じである．これを実行するために， In [8] を用意する．

さらに， \begin{equation*} \frac{u^{n+1}_i-\frac{u^n_{i-1}+u^n_{i+1}}{2}}{\tau} +c \frac{u_{i+1}^n-u_{i-1}^n}{2h}=0, \end{equation*} すなわち， \begin{equation} \tag{B.8} u^{n+1}_i=\frac{1+\mu}{2}u^n_{i-1}+\frac{1-\mu}{2}u_{i+1}^n \end{equation} をLax--Friedrichs (LF) 差分スキームと言う．これを実行するために， In [9] を用意する．

In [8]:  
#線形移流方程式に対する風上差分スキーム
def linear_advection_upwind(c, initial, N, T, abslam, num):
  L = 1.0
  h = L/N
  tau = abslam*h/np.abs(c)
  nmax = int(T/tau)
  step = int(max(1, nmax/num))
  lam = c*tau/h
  theta = 1 if c >= 0 else 0

  xgrid = np.linspace(0.0, L, N)
  xtmp = np.copy(xgrid[0:N-1])
  tgrid = np.array([0.0])
  u = initial(xtmp)
  sol = np.copy(np.append(u,u[0]))

  for n in range(nmax):
    u = (1.0 - theta*lam + (1.0 - theta)*lam)*u + theta*lam*(np.roll(u,1)) - (1.0 - theta)*lam*(np.roll(u,-1))
    tnow = (n+1)*tau
    if (n+1)%step==0:
      sol=np.vstack((sol,np.append(u,u[0])))
      tgrid=np.append(tgrid, tnow)

  return xgrid, tgrid, sol

In [9]:  
#線形移流方程式に対するLax--Friedrics差分スキーム
def linear_advection_lax(c, initial, N, T, abslam, num):
  L = 1.0
  h = L/N
  tau = abslam*h/np.abs(c)
  nmax = int(T/tau)
  step = int(max(1, nmax/num))
  lam = c*tau/h

  xgrid = np.linspace(0.0, L, N)
  xtmp = np.copy(xgrid[0:N-1])
  tgrid = np.array([0.0])
  u = np.vectorize(initial)(xtmp)
  sol = np.copy(np.append(u,u[0]))

  for n in range(nmax):
    u = 0.5*(1.0 + lam)*np.roll(u,1) + 0.5*(1.0 - lam)*np.roll(u,-1)
    tnow = (n+1)*tau
    if (n+1)%step==0:
      sol=np.vstack((sol,np.append(u,u[0])))
      tgrid=np.append(tgrid, tnow)

  return xgrid, tgrid, sol

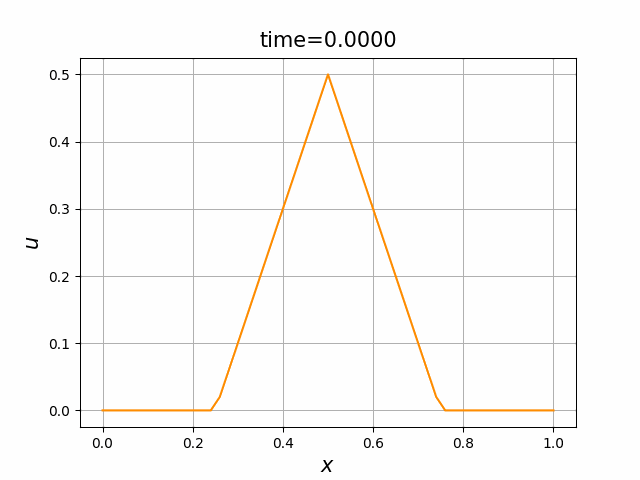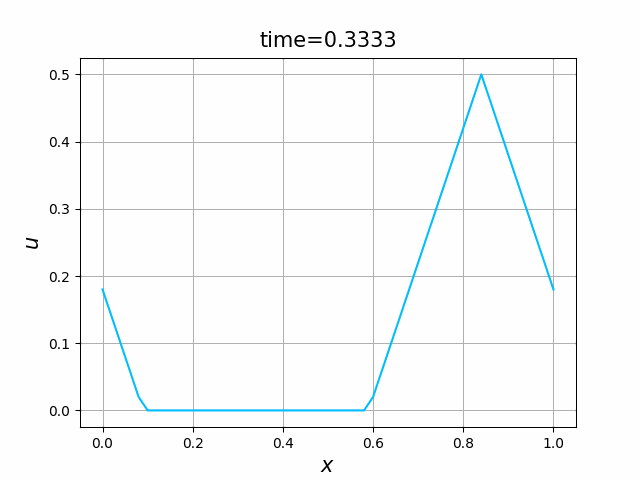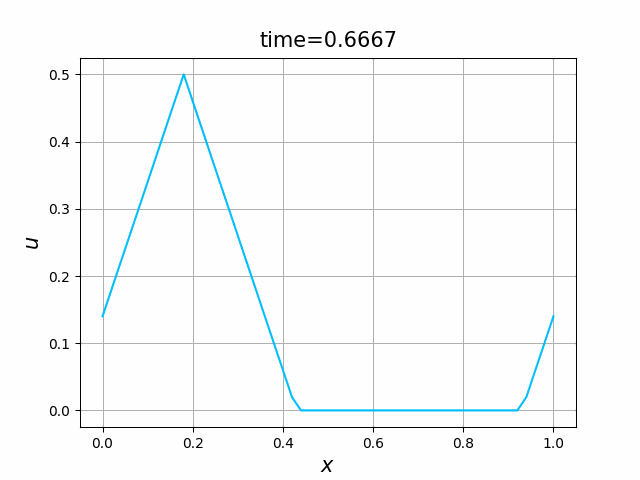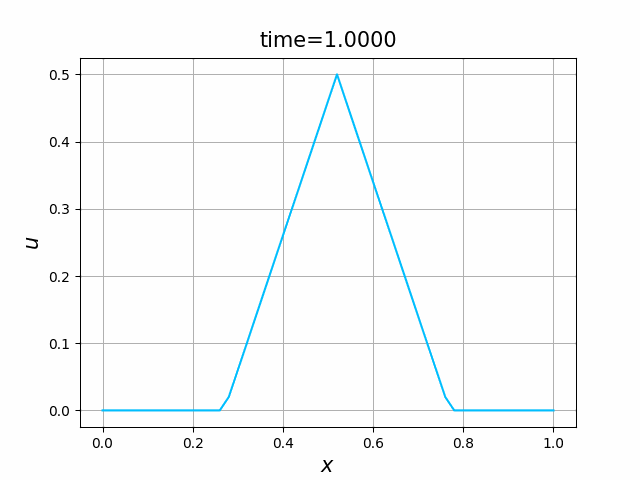
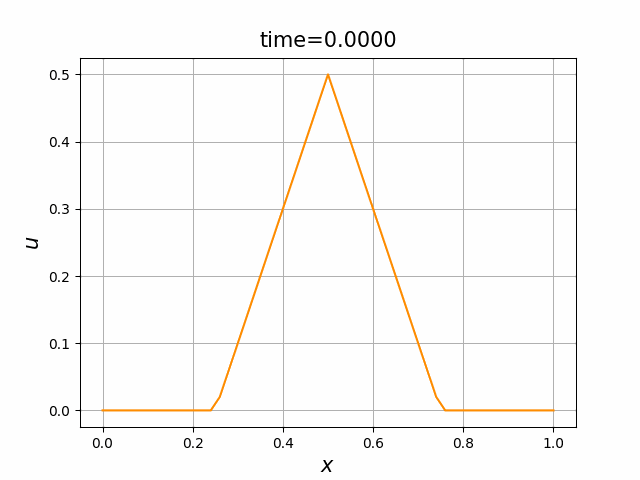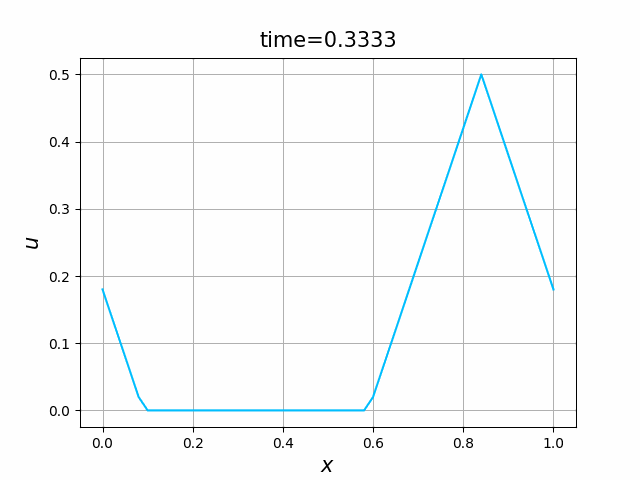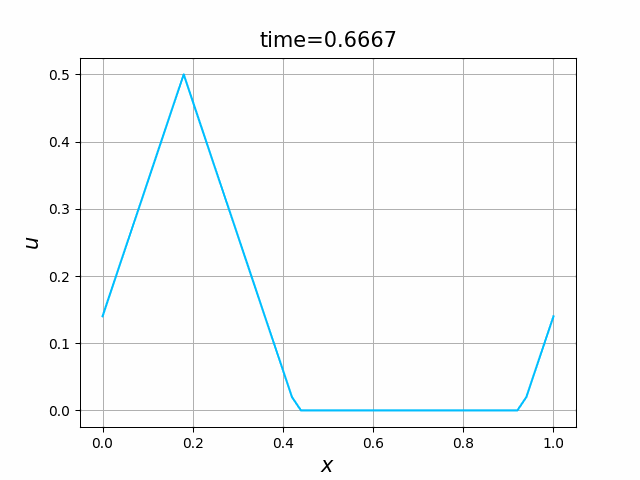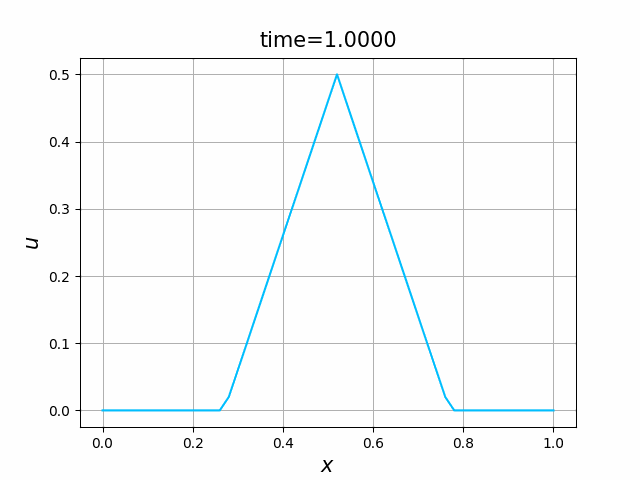
これらを次の In [10] のように実行する．風上差分スキーム(B.7)について，図B.3が$a_1$，図B.4が$a_2$を用いた計算結果である． LF差分スキーム(B.8)について，図B.5が$a_1$，図B.6が$a_2$を用いた計算結果である．

In [10]:
# 初期値
def initial1(x):
  return np.sin(4*np.pi*x)

def initial2(x):
  return np.maximum(0.0, np.minimum(2.0*x-0.5, 1.5-2.0*x))

#パラメータの設定
c = 1.0
N = 51
T = 1.0
abslam = 1
num = 40

#線形移流方程式の計算
x, tn, sol = linear_advection_upwind(c, initial1, N, T, abslam, num)
#x, tn, sol = linear_advection_lax(c, initial1, N, T, abslam, num)

#図の表示
plot_solution(x, sol)

#アニメーションを表示
anim = plot_animation(x, tn, sol)
#結果をadvection.gifに保存（Googleドライブをマウントしておくこと！）
anim.save('/content/drive/MyDrive/Colab Notebooks/fig/advection.gif', writer='pillow')
rc('animation', html='jshtml')
plt.close()
anim

変数係数の場合

引き続き，変数係数の線形移流方程式を考えよう： \begin{align} u_t+f(x,t)u_x&=g(x,t),&& x\in \mathbb{T},~t\in (0,T),\tag{B.9a}\\ u(x,0)&=a(x),&& x\in \mathbb{T}.\tag{B.9b} \end{align} ここで， $f:\mathbb{R}\times [0,T]\to\mathbb{R}$， $g:\mathbb{R}\times [0,T]\to\mathbb{R}$， ${a}:\mathbb{R}\to\mathbb{R}$ は与えられた関数である．

\begin{equation} f_i^n=f(x_i,t_n),\quad g_i^n=g(x_i,t_n) \end{equation} とおく．さらに， \begin{equation} [s]_+=\max\{s,0\},\quad [s]_-=\max\{-s,0\},\quad s=[s]_+-[s]_{-} \end{equation} と記号を定め， \begin{equation} f_i^{n,+}=[f_i^n]_+,\quad f_i^{n,-}=[f_i^n]_-,\quad f_i^n=f_i^{n,+}-f_i^{n,-} \end{equation} と書く．

(B.9)に対する風上スキームは， \begin{equation*} \frac{u^{n+1}_i-u_i^n}{\tau}+ f_i^{n,+}\frac{u_{i}^n-u_{i-1}^n}{h}- f_i^{n,-}\frac{u_{i+1}^n-u_{i}^n}{h}=g_i^n \end{equation*} となる．すなわち， \begin{equation} \tag{B.10} u^{n+1}_i = u_i^n-f_i^{n,+}\frac{\tau}{h}(u_{i}^n-u_{i-1}^n)+ f_i^{n,-}\frac{\tau}{h}(u_{i+1}^n-u_{i}^n)+\tau g_i^n \end{equation} となる．初期条件は，(B.4)と同じである．これを実行するために， In [11] を用意する．

(B.9)に対するLFスキームは， \begin{equation*} \frac{u^{n+1}_i-\frac{u^n_{i-1}+u^n_{i+1}}{2}}{\tau} +f_i^{n}\frac{u_{i+1}^n-u_{i-1}^n}{2h}=g_i^n \end{equation*} すなわち， \begin{equation} u_i^{n+1} =\frac{u_{i-1}^n+u_{i+1}^n}{2}- f_i^{n}\frac{\tau}{2h}(u_{i+1}^n-u_{i-1}^n)+\tau g_i^n \tag{B.11} \end{equation} となる．初期条件は，(B.4)と同じである．これを実行するために， In [12] を用意する．

In [11]: 
#変数係数線形移流方程式に対する風上差分スキーム
def variable_advection_upwind(func_f, fmax, func_g, initial, N, T, abslam, num):
  L = 1.0
  h = L/N
  tau = abslam*h/fmax
  nmax = int(T/tau)
  step = int(max(1, nmax/num))
  mu = tau/h
  theta = 1 if c >= 0 else 0

  xgrid = np.linspace(0.0, L, N)
  xtmp = np.copy(xgrid[0:N-1])
  tgrid = np.array([0.0])
  u = initial(xtmp)
  sol = np.copy(np.append(u,u[0]))

  tnow = 0.0
  for n in range(nmax):
    coef_f = func_f(xtmp, tnow)
    coef_fp = np.maximum(coef_f, 0.0)
    coef_fm = np.maximum(-coef_f, 0.0)
    coef_g = func_g(xtmp, tnow)
    u = u - mu*coef_fp*(u - np.roll(u,1)) + mu*coef_fm*(np.roll(u,-1) - u) + tau*coef_g
    tnow = (n+1)*tau
    if (n+1)%step==0:
      sol=np.vstack((sol,np.append(u,u[0])))
      tgrid=np.append(tgrid, tnow)

  return xgrid, tgrid, sol

In [12]:  
#変数係数線形移流方程式に対するLF差分スキーム
def variable_advection_lax(func_f, fmax, func_g, initial, N, T, abslam, num):
  L = 1.0
  h = L/N
  tau = abslam*h/fmax
  nmax = int(T/tau)
  step = int(max(1, nmax/num))
  mu = tau/h
  theta = 1 if c >= 0 else 0

  xgrid = np.linspace(0.0, L, N)
  xtmp = np.copy(xgrid[0:N-1])
  tgrid = np.array([0.0])
  u = initial(xtmp)
  sol = np.copy(np.append(u,u[0]))

  tnow = 0.0
  for n in range(nmax):
    coef_f = func_f(xtmp, tnow)
    coef_g = func_g(xtmp, tnow)
    u = 0.5*(np.roll(u,-1) + np.roll(u,1)) - 0.5*mu*coef_f*(np.roll(u,-1) - np.roll(u,1)) + tau*coef_g
    tnow = (n+1)*tau
    if (n+1)%step==0:
      sol=np.vstack((sol,np.append(u,u[0])))
      tgrid=np.append(tgrid, tnow)

  return xgrid, tgrid, sol

初期関数と係数関数を， \begin{align} a(x)&=a_3(x) =\sin(2\pi x),\tag{B.6a}\\ f(x,t)&=f_3(x,t) =1\tag{B.6b}\\ g(x,t)&=g_3(x) =0\tag{B.6c} \end{align} と選ぶ．すると，(B.9)の厳密解は， \begin{equation} u(x,t) =\sin(2\pi (x-t))\tag{B.7} \end{equation} となる．また，初期関数と係数関数を， \begin{align} a(x)&=a_4(x) =\sin(2\pi x),\tag{B.8a}\\ f(x,t)&=f_4(x,t) =\cos(2\pi x)\tag{B.8b}\\ g(x,t)&=g_4(x) =-2\pi \cos(2\pi(x-t))+2\pi\cos(2\pi x)\cos(2\pi(x-t)) \tag{B.8c} \end{align} と選んでも，(B.9)の厳密解は，(B.7)である． In [11] （風上スキーム）を実行してみる．図B.7が，(B.6)を持ちいたとき，図B.8が，(B.8)を持ちいたときの結果である．

In [13]:  
# 初期値
def initial1(x):
  return np.sin(2*np.pi*x)

def func_f1(x, t):
  return np.ones(len(x))
  
def func_g1(x, t):
  return np.zeros(len(x))
  
#パラメータの設定
fmax = 1.0 #これは自分で設定する．（この部分をプログラム化しても良い）
N = 51
T = 1.0
abslam = 1.0
num = 40

#変数係数線形移流方程式の計算
x, tn, sol = variable_advection_upwind(func_f1, fmax, func_g1, initial1, N, T, abslam, num)
#x, tn, sol = variable_advection_lax(func_f1, fmax, func_g1, initial1, N, T, abslam, num)

#図の表示
plot_solution(x, sol)

#アニメーションを表示
anim = plot_animation(x, tn, sol)
#結果をadvection.gifに保存（Googleドライブをマウントしておくこと！）
anim.save('/content/drive/MyDrive/Colab Notebooks/fig/advection.gif', writer='pillow')
rc('animation', html='jshtml')
plt.close()
anim

図C.1 — 図C.7 Out [13] 風上差分スキームの結果．初期値$a=a_3$, $f=f_3$, $g=g_3$, $N=51$，$T=1$

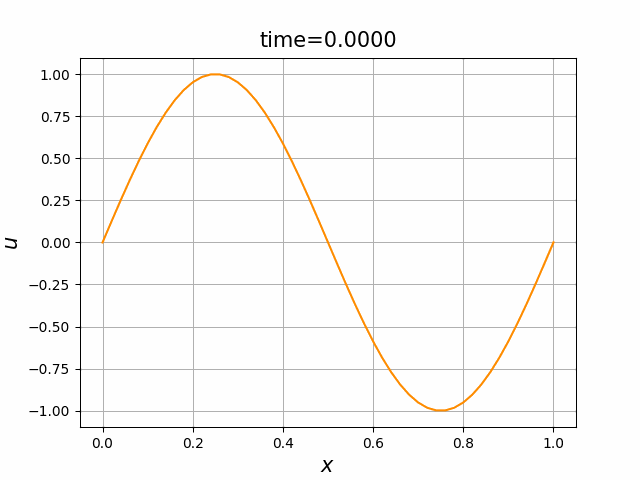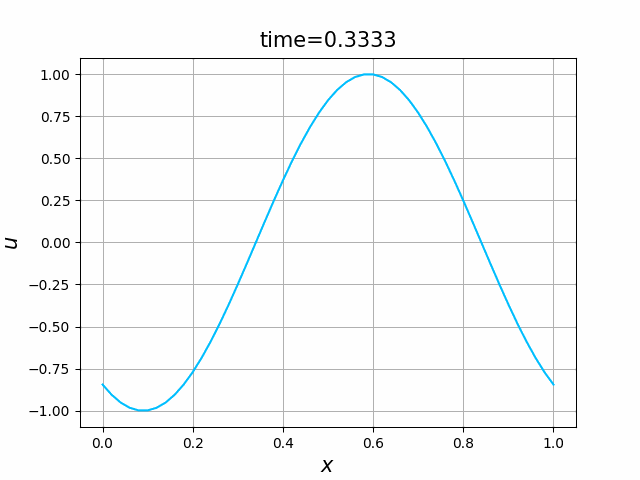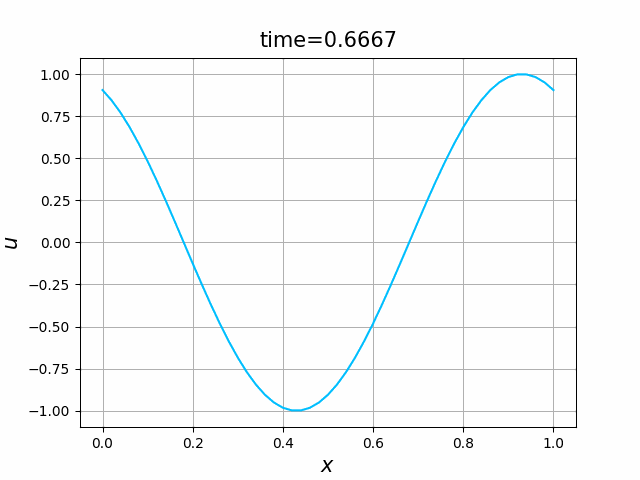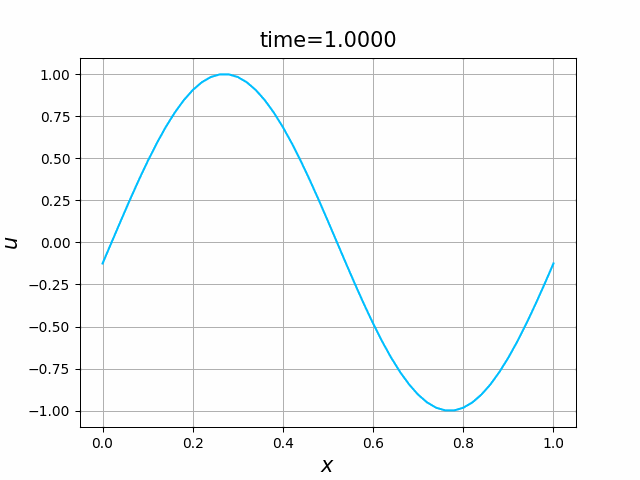
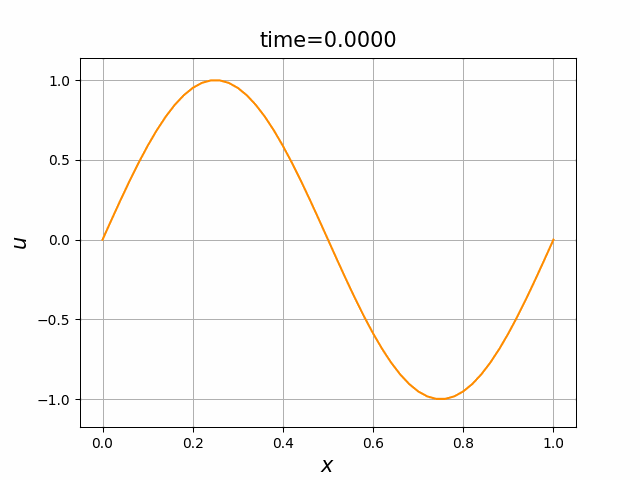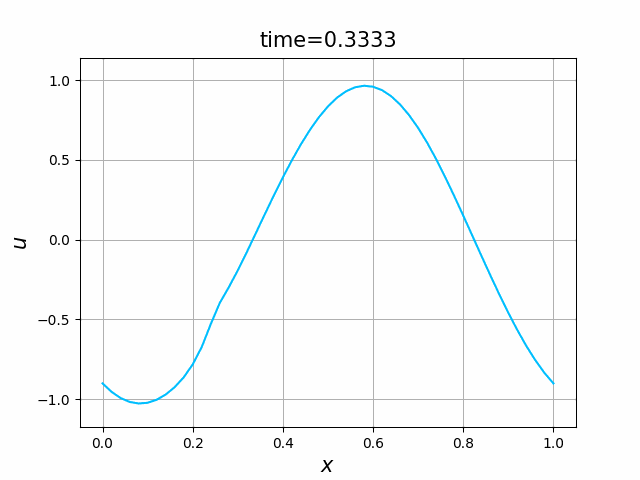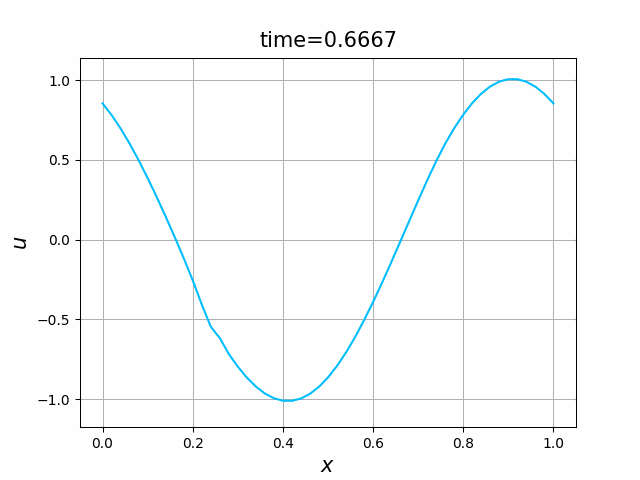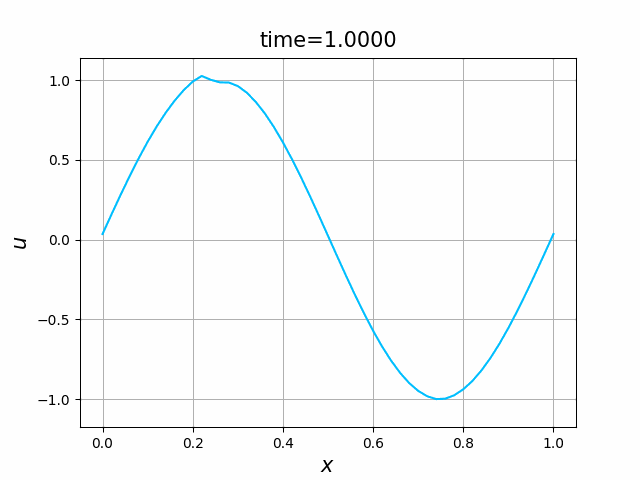
図C.7と図C.8を比べると，厳密解は同じであるが，変数係数の場合の方が，誤差は大きくなっているようである．

そこで，誤差を詳しく調べてみよう．次を講義で示した．

定理． 変数係数の線形移流方程式の初期値問題(C.9)の解 $u$ は，$Q=\mathbb{T}\times [0,T]$ 上で $C^2$ 級とする．このとき，風上スキーム(C.10)の解 $u_i^n$ について，条件 \[ \|f\|_{\infty}\frac{\tau}{h}\le 1 \] の下で， \[ \max_{0\le t_n\le T}\|\boldsymbol{e}^{(n)}\|_\infty\le h \|f\|_\infty\frac{T}{2}\left(\|u_{tt}\|_{\infty}+ \|u_{xx}\|_{\infty}\right) \] が成り立つ．ただし， $\boldsymbol{e}^{(n)}=(e_1^n,\ldots,e_N^n)$， $e_i^n = u_i^n - u(x_i,t_n)$ である．

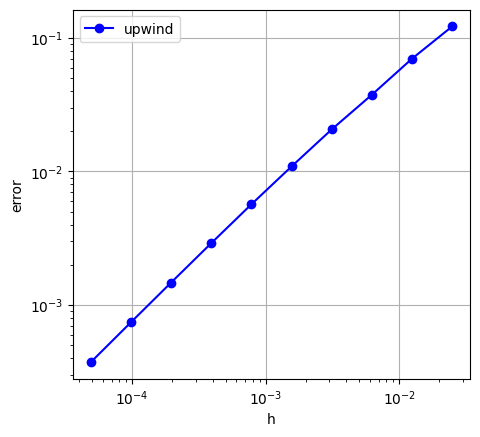
これを計算で確かめるために，In [14]を用意する．説明は，Aですでに述べた通りである．風上差分スキームに対して，In [15]のように実行する．Out [15]を見ると，分割が荒いときには十分な精度は出ていないが，分割を細かくすると，期待する $O(h)$ に近づくことがわかる．

In [14]:  
#誤差の計算、変数係数線形移流方程式
def error_advection(L, func_f, fmax, func_g, initial, exact_sol, abslam):
  T = 1.0
  lam = 1.0
  N = 20
  num = 40

  kmax = 10
  hv = np.zeros(kmax)
  ev = np.zeros(kmax)

  for k in range(kmax): 
    N = N*2
    x, tn, sol = variable_advection_upwind(func_f, fmax, func_g, initial, N, T, abslam, num)
    #x, tn, sol = variable_advection_lax(func_f, fmax, func_g, initial, N, T, abslam, num)
    err = 0.0
    for n in range(tn.shape[0]):
      tval = tn[n]
      err = np.maximum(err, np.linalg.norm(sol[n,:] - exact_sol(x, tval), ord=np.inf))
    hv[k] = L/N
    ev[k] = err

  rate=(np.log(ev[1:]) - np.log(ev[:-1])) / (np.log(hv[1:]) - np.log(hv[:-1]))
  
  return hv, ev, rate

In [15]:
# 初期値
def initial4(x):
  return np.sin(2*np.pi*x)

def func_f4(x, t):
  return np.cos(2.0*np.pi*x)

def func_g4(x, t):
  return -2.0*np.pi*np.cos(2.0*np.pi*(x - t)) + np.cos(2.0*np.pi*x)*2.0*np.pi*np.cos(2.0*np.pi*(x-t))
  
def solution(x, t):
  return np.sin(2.0*np.pi*(x - t))

#パラメータの設定
L = 1.0
T = 1.0
abslam = 1.0
fmax = 1.0

#変数係数移流方程式の計算
hv, ev, rate = error_advection(L, func_f4, fmax, func_g4, initial4, solution, abslam)

#収束の速さの出力
for i in range(rate.shape[0]-1):
  print(f'{hv[i+1]:.3f}, {rate[i]:.3f}')

#結果の描画（両対数目盛）
plt.plot(hv, ev, 'bo-')   
plt.xscale('log')
plt.yscale('log')
plt.legend(['explicit'])  
plt.xlabel('h')
plt.ylabel('error')
plt.grid('on')
plt.gca().set_aspect('equal', adjustable='box') 
plt.show()  

Out [15]: 
0.013, 0.803
0.006, 0.898
0.003, 0.864
0.002, 0.922
0.001, 0.943
0.000, 0.968
0.000, 0.981
0.000, 0.989

問題

上記の入力と出力をすべて確かめよ．
パラメータ値を変えて，計算を再試行せよ．
例題を自分で設定して，上記の方法を試せ．

課題

課題B.1

自分で例題を設定して，変数係数線形移流方程式に対するLax--Friedrichs差分スキームの誤差の減衰の速さについて調べよ．すなわち，風上差分スキームに対するOut [15]に相当する計算を行え．

参考文献

[FF2014] M. Falcone and R. Ferretti, Semi-Lagrangian Approximation Schemes for Linear and Hamilton--Jacobi Equations, Society for Industrial and Applied Mathematics (SIAM), 2014.