群と幾何学

図形のもつ対称性は、その図形をそれ自身にうつすような合同変換全体によって記述される。このような合同変換全体は、「群」とよばれる代数系をなす。
群とは、結合則をみたす演算が定義されていて、この演算についての単位元が存在し、さらにすべての要素が逆元をもつような集合である。
群の概念は、数学のあらゆる分野に登場するが、歴史的には、19世紀はじめに、フランスの数学者ガロアが方程式のもつ対称性の群に注目して、5次以上の方程式は、一般に根号によって解く公式がないことを証明したことに由来する。
この講義では,主に平面の合同変換からなる群を扱う.
課題1 平面の合同変換は,直線に関する対称移動(鏡映変換)を高々3個合成して
得られることを示せ.
また,この事実を3次元ユークリッド空間の合同変換に拡張せよ.
さらに,一般のn次元ユークリッド空間の合同変換について考察せよ.
Gを平面のいくつかの合同変換からなる群とする.
Gが離散的であるとは,平面の任意の点Pに対して,PにGの要素をほどこすことによって
得られる点列が集積点をもたないことである.
Gが固定点をもたないとは,
平面の任意の点Pに対して,点Pをそれ自身に移すGの要素が恒等変換のみであることである.
課題2 数直線をそれ自身に移す合同変換群で,離散的かつ固定点をもたないものは
どのような変換群かを調べよ.
一般に,平面の合同変換群で,向きを保ち,離散的かつ固定点をもたないものは
どのようなものがありうるかを調べよ.
向きを保たないものについても考察せよ.
局所的には「ユークリッド平面と合同」な幾何構造
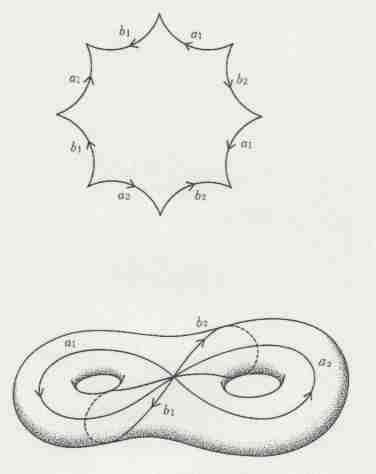
下のトーラスの図を見てみよう.これは3次元ユークリッド空間の中では”曲がった”形で表現されているが,
トーラスを2方向の回転角でパラメータ表示して,この座標で長さを測ると,トーラスの正確な
”地図”を平面上に描くことができる.
このような意味で,トーラスには局所的には「ユークリッド平面と合同」な幾何構造を与えることができる.
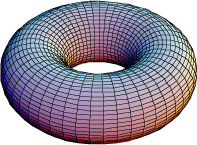
平面の合同変換群で,離散的で固定点をもたないものを考えることにより,局所的には「ユークリッド平面と合同」な距離の構造をもつ「曲面」をつくることができる.トーラスは平面の2つの方向の平行移動で生成される
群に対応している.
逆に,このような性質をもった曲面で”端”のないものは
すべて平面の合同変換群から構成することができる.講義ではこのような事実を直観的に説明する.
固定点をもつものも許すと,平面の合同変換群の離散的な部分群は17通りに分類される.
これらは平面の連続模様のパターンに対応する。次のサイトを参照してみよう。
模様の幾何学
Symmetric
tiling
Introduction to symmetry
タイルばりのパターン
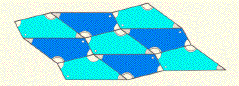
下の図は合同な4角形によって平面全体を互いに重ならないように敷き詰めたものである。このようなパターンはタイルばりとよばれる。対称性を記述する群の観点からタイルばりについて見ていこう。
課題3 平面を合同な正多角形でうめつくすタイルばりのパターンを分類せよ.
また,2種類の正多角形でうめつくうパターンはどのようなものがありうるかを考察せよ.
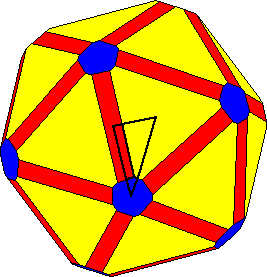
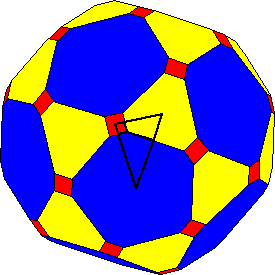
次のパターンは球面のタイルばりを与える。
これは内角が90度,60度,36度の大円弧で囲まれる3角形による球面のタイルばりに
由来する.
Geometry Centerの次のサイトは,タイルばりについてのより詳しい情報を与えてくれる.
Tiling
課題4 球面の大円弧で囲まれる3角形(球面3角形)の面積を内角で表せ.
内角が π/p, π/q, π/r (p, q, rは整数)の球面三角形によって
球面がタイルばりされるような
p, q, rはどのような可能性があるかを調べよ.
双曲平面のタイルばり
講義ではさらに,ロバチェフキー,ボヤーイらによる非ユークリッド幾何学の発見の歴史にふれる.
下の図はポアンカレによる非ユークリッド幾何学のモデルである.
局所的にこのようなモデルと合同な幾何構造は「双曲幾何」とよばれる.
種数が2以上の曲面は双曲幾何構造をもち,
ポアンカレのモデルの離散的な合同変換群を用いて表されることを説明する.

参考文献
[1] 原田耕一郎 「群の発見」 岩波書店
[2] 志賀浩二 「群論30講義」 朝倉書店
[3] H. Weyl, Symmetry, Princeton University Press(邦訳 紀伊国屋書店)
[4] 小林昭七 「ユークリッド幾何から現代幾何へ」(日本評論社)
[5] ニクリン,シャファレヴィッチ著,根上訳 「幾何学と群」(シュプリンガー東京)
[6] 河野俊丈 「曲面の幾何構造とモジュライ」(日本評論社)







