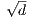If you wish to join the seminar, please write an email to shane.kelly.uni - at - gmail - dot - com and cc to shanekelly64 - at - gmail - dot - com

Contents

“Abstract”

Harvard Business Review called Data Scientist “The Sexiest Job of the 21st Century”, and indeed, the field of data science is evolving into one of the fastest-growing and most in-demand disciplines in the world. The enhanced ability to observe, collect and store data in settings from business to government, health care to academia, promises to revolutionise these industries.

In this seminar, we will cover some of the mathematical foundations of data science.

Topics will be chosen by the students from among the following (there will be multiple lectures per topic):

Machine Learning, Clustering, Belief Propagation, Compressed Sensing, Topic Models, Hidden Markov Process, Graphical Models, High Dimensional Probability, Random Graphs.

General information

About the presentation

This is a student seminar which means that the students each make one of the presentations. The presentation should be about 75 minutes long, leaving 15 minutes for potential questions and discussion.

Students are not required to hand in any written notes. However, students are encouraged to prepare some notes if they feel it will improve the presentation. This should be considered seriously, especially if the student has not made many presentations before.

For example, its helpful to have

1. a written copy of exactly what they plan to write on the blackboard, and
2. 5-10 pages of notes on the material to help find any gaps in your understanding.

If notes are prepared I will collect them and give feedback if desired.

The material listed below should be considered as a skeleton of the talk, to be padded out with other material from the texts or examples that the student finds interesting, relevant, enlightening, useful, etc.

If you have any questions please feel free to contact me at the email address above.

Contents

Overview

19.10 First meeting

26.10 Preparation

I. 02.11 (Aizhan) High dimensional probability I: The law of large numbers and geometric aspects

When n is very large, the euclidean space ℝ^d exhibits properties which seem counter-intuitive to our experience with ℝ² and ℝ³. For example, almost all the volume is concentrated near the boundary, the volume approaches zero as d becomes large, and if we chose a point at random on the surface for the “north pole”, then most of the volume is concentrated around the equator. This lecture discusses these phenomena, and also includes the law of large numbers, which is a vast generalisation of the fact that with two die, you are more likely to role a 7 than a 2 or a 12.

This lecture will discuss the law of large numbers, the geometry of high dimensions, properties of the unit ball, and generating points uniformly at random from a ball.

Reference: Sections 2.1, 2.2, 2.3, 2.4, 2.5 of “Foundations of Data Science”, Blum, Hopcroft, Kannan

II. 09.11 (Niall) High dimensional probability II: Gaussians

This lecture discusses consequences of the geometry discussed in the previous lecture. For example, in high dimensions d, almost all of the volume of the Gaussian distribution is concentrated around a sphere of radius 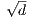. One deduces from this that a randomly chosen projection to a smaller dimensional space will preserve distance with high probability.

This lecture will discuss Gaussians in high dimensions, random projection and the Johnson-Lindenstrauss lemma, separating Gaussians, and fitting a single spherical Gaussian to data.

Reference: Sections 2.6, 2.7, 2.8, 2.9 of “Foundations of Data Science”, Blum, Hopcroft, Kannan

III. 16.11 (David Hinrichs) Random Graphs I: The G(n,p) Model

Large graphs appear in many contexts such as social networks (both online and offline), journal citations, neuroscience, protein interactions, linguistics, and many other places. The recent study of statistical properties of large graphs is similar to the switch in physics from mechanics to statistical mechanics.

The G(n,p) model is a random graph with n vertices, and an edge between two given vertices with probability p. This lecture studies statistical properties of such graphs such as the degree distribution, and the existence of triangles.

This lecture will discuss the G(n,p) model.

Reference: Section 8.1 of “Foundations of Data Science”, Blum, Hopcroft, Kannan

IV. 23.11 (Gus) Random Graphs II: Phase Transitions

As the edge probability p of G(n,p) random graphs varies, many properties undergo abrupt changes at certain values. For example, as p reaches 1∕n, there is a sudden emergence of cycles, and at p = 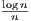there is a sudden disappearance of isolated vertices. The most important is perhaps the appearance of a giant component at p = 1∕n. This lecture discusses such phenomena.

This lecture will discuss phase transitions.

Reference: Section 8.2 of “Foundations of Data Science”, Blum, Hopcroft, Kannan

V. 30.11 (Jakob) Random Graphs III: The Giant Component

A seminal result in random graph theory is the almost certain existence of a giant component containing a number of vertices proportional to the total number of vertices. These giant components appear in many real world graphs. This lecture discusses things like the probability that there is a giant component, and the number of vertices it is likely to have.

This lecture will discuss the giant component.

Reference: Section 8.3 of “Foundations of Data Science”, Blum, Hopcroft, Kannan

VI. 07.12 (Vanessa Stechert) Random Graphs IV: Branching processes, cycles, and full connectivity

A branching process is a method for creating a random tree. An easy case is when the distribution of the number of children at each node in the tree is the same. A basic question is: what is the probability that the tree is finite? This discusses these questions, as well as the questions: when do cycles form in random graphs, and when do the graphs become fully connected?

This lecture will discuss branching processes, and cycles and full connectivity.

Reference: Sections 8.4, 8.5 of “Foundations of Data Science”, Blum, Hopcroft, Kannan

VII. (unassigned) Random Graphs V: Increasing properties, nonuniform models, and growth models

An increasing property is a property which doesn’t disappear from a graph after adding an edge. Examples include being connected, and having a cycle. The first topic of this lecture is showing that any increasing property has a threshold. The second topic is studying phase transitions from satisfiable to unsatisfiable for certain randomly generated Boolean formulas. Since this is also an increasing property, the techniques developed for graphs can be applied. The lecture finishes with a discussion of random graph models which are harder to analyse than G(n,p), but which resemble real world graphs more closely.

This lecture will discuss phase transitions, nonuniform models and growth models of random graphs.

Reference: Sections 8.5, 8.6, 8.7, 8.8 of “Foundations of Data Science”, Blum, Hopcroft, Kannan

VIII. (unassigned) Random Graphs VI: Growth models and small world graphs

In the world, many graphs start as small graphs that grow over time. The first topic of this lecture is modelling such random graphs. The second topic discusses graphs whose edges can be classified into “short distance” and “long distance” and finding short paths between two vertices using only local information.

This lecture will discuss growth models, and small world graphs.

Reference: Sections 8.9, 8.10 of “Foundations of Data Science”, Blum, Hopcroft, Kannan

IX. 14.12 (Franziska Boenisch) Machine Learning I: Introduction, and batch learning

This lecture will give an introduction to the core problem of machine learning, discuss overfitting and uniform convergence, give some examples, and discuss regularization.

Reference: Sections 5.1, 5.2, 5.3, 5.4 of “Foundations of Data Science”, Blum, Hopcroft, Kannan

X. 11.01 (Shane) Machine Learning II: online learning, the perceptron algorithm, and kernel functions

This lecture will discuss online learning and the Perceptron algorithm, kernel functions, online to batch conversion, and support-vector machines.

XI. 18.01 (Hassan) Machine Learning III: VC-Dimension

This lecture will discuss VC-Dimension.

Reference: Section 5.9 of “Foundations of Data Science”, Blum, Hopcroft, Kannan

XII. 25.01 (Mohammed) Machine Learning IV: Boosting, SGD, combining experts, and deep learning

This lecture will cover Strong and weak learning and boosting, stochastic gradient descent, the combining-sleeping-experts-algorithm, and deep learning.

Reference: Sections 5.10, 5.11, 5.12, 5.13 of “Foundations of Data Science”, Blum, Hopcroft, Kannan

XIII. 01.02 (Christoph Brockmann) Clustering I: Center-based methods

This lecture will give an introduction to clustering, discuss k-means clustering, k-center clustering, and spectral clustering.

Reference: Sections 7.1, 7.2, 7.3, 7.4, 7.5 of “Foundations of Data Science”, Blum, Hopcroft, Kannan

XIV. 08.02 (Viktor) Clustering II: Approximation stability, high-density clusters, and sparse graph cuts

This lecture will cover spectral clustering, high-density clusters, kernel methods, and recursive clustering based on sparse cuts.

Reference: Sections 7.6, 7.7, 7.8, 7.9 of “Foundations of Data Science”, Blum, Hopcroft, Kannan

XV. 15.02 (Achille Mbope) Clustering III: Community finding, and social networks

Reference: Sections 7.10, 7.11, 7.12 of “Foundations of Data Science”, Blum, Hopcroft, Kannan

XVI. TBA (Yurong Ding) Model Fitting I: Topic models and hidden Markov models

This lecture will cover topic models, hidden Markov models, graphical models and belief propogation, and Bayesian networks.

Reference: Sections 9.1, 9.10, 9.11, 9.12 of “Foundations of Data Science”, Blum, Hopcroft, Kannan

XVII. TBA (Moritz) Model Fitting II: Graphical models

This lecture will cover Markov random fields, factor graphs, tree algorithms, message passing in general graphs, graphs with a single cycle, and belief update in networks with a single loop.

Reference: Sections 9.13, 9.14, 9.15, 9.16, 9.17, 9.18 of “Foundations of Data Science”, Blum, Hopcroft, Kannan

XVIII. (unassigned) Model Fitting III: Maximum weight matching and correlation between variables

This lecture will cover maximum weight matching, warning propagation, and correlation between variables.

Reference: Sections 9.19, 9.20, 9.21 of “Foundations of Data Science”, Blum, Hopcroft, Kannan