


Next: About this document ...
数学解析 予定表
ルベーグ積分の知識があるのが望ましいが、
以下の の項目は、ルベーグ積分を知っておくのが
よい項目、
の項目は、ルベーグ積分を知っておくのが
よい項目、 の項目は理解にルベーグ積分の知識が
必要な項目です。
の項目は理解にルベーグ積分の知識が
必要な項目です。
0. なぜ、関数解析が必要か?
1. 位相の復習
距離空間, 開集合, 閉集合, 位相の強弱,
コンパクト性, 完備性, etc.
2. ノルム空間
- (1)
- ノルムの定義
- (2)
 Holderの不等式、Minkowskiの不等式
Holderの不等式、Minkowskiの不等式
- (3)
 lp, Lp
lp, Lp
- (4)
- ノルム空間の位相
- (5)
- 可分性
- (6)
- Weierstrassの多項式近似定理(確率論を用いたBernsteinの証明)
- (7)
- Banach空間の定義、例
- (8)
- ノルム空間の完備化
(
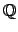 の完備化から
の完備化から
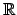 を作ったように、
完備でないノルム空間は適当に元を加えて完備な空間にできる。
を作ったように、
完備でないノルム空間は適当に元を加えて完備な空間にできる。
![$C([0,1]\to {\mathbb R})$](img7.gif) をLpの位相でこの
方法で完備化したものの具体的な表現が
をLpの位相でこの
方法で完備化したものの具体的な表現が
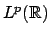 だと言える)
だと言える)
3. ヒルベルト空間
- (1)
- プレヒルベルト空間: 定義と例
- (2)
 ヒルベルト空間の定義, 例、l2, L2
ヒルベルト空間の定義, 例、l2, L2
- (3)
- 完全正規直交系(=CONS)とその性質
- (4)
- CONS, 例、Fourier級数、Hermite多項式
固有関数の視点、対称行列の異なる固有値に対応する固有ベクトルは
直交すること。
- (5)
- Parsevalの等式、Besselの不等式
- (6)
- CONSの存在
- (7)
- 直交射影、凸集合の場合への拡張を注意
- (8)
- 直交補空間
- (9)
-
 条件つき平均値、マルチンゲールの定義と直交射影との関連
条件つき平均値、マルチンゲールの定義と直交射影との関連
5. 有界線形作用素
- (1)
- 定義と性質
- (2)
- 有界線形作用素全体が作用素ノルムでBanach空間になること
- (3)
- 有界線形作用素の例
(合成積による作用素、ハウスドルフ・ヤングの不等式
 、マルコフ半群
についての注意)
、マルコフ半群
についての注意)
- (4)
- Rieszの表現定理
- (5)
-
 共役空間(双対空間)の定義と例
(
共役空間(双対空間)の定義と例
(
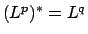 ただし、
ただし、
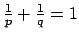 ,
,
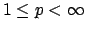 一般には
一般には
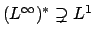 ).
).
- (6)
-
 Radon-Nykodimの定理(Rieszの表現定理の応用)
Radon-Nykodimの定理(Rieszの表現定理の応用)
- (7)
- Neumann級数と積分方程式(とくにVolterra型について)
- (8)
- 縮小写像の原理とその応用例
6. 非有界作用素
- (1)
- 閉作用素、可閉作用素の定義、例
- (2)
- 随伴作用素、自己共役作用素
- (3)
- スペクトル集合、レゾルベント集合
(例、Volterra型積分作用素)
- (4)
- コンパクト作用素の定義、スペクトルに対する注意
- (5)
-
 自己共役作用素のスペクトル分解の注意
自己共役作用素のスペクトル分解の注意
測度論の参考書は
1. 「ルベーグ積分」 (竹之内脩著, 培風館)
2. 「ルベーグ積分入門」(伊藤清三著, 裳華房)
3. 「ルベーグ積分から確率論」(志賀徳造著、共立出版)
4. 「確率論」(伊藤雄二著、朝倉書店)
関数解析の参考書としてシラバスにあげた以外に
1. Functinal Analysis, Reed-Simon著, Academic Press
2. 「ヒルベルト空間と量子力学」 新井朝雄著, 共立出版
3. 「フーリエ解析と関数解析学」 新井仁之著、培風館
が参考になる。1,2 ともに量子力学を意識した内容の本である。
1はMethods of Modern Mathematical Physicsの4巻本の最初の
1冊目で2冊目以後も面白い本です。
3はフーリエ解析、ウエイブレットについても触れられている。
やはり、ヒルベルト空間について書かれた本。
Shigeki Aida
2003-04-09
![]() の項目は、ルベーグ積分を知っておくのが
よい項目、
の項目は、ルベーグ積分を知っておくのが
よい項目、![]() の項目は理解にルベーグ積分の知識が
必要な項目です。
の項目は理解にルベーグ積分の知識が
必要な項目です。